- #1
pabilbado
Gold Member
- 17
- 1
I was just wondering about the path an orbiting particle takes when it's center of circular motion also translates. So as to calculate the distance traveled I know I have to get a function that relates velocity with respect to time and integrate it, but I can't doit, I get stuck integrating. I have search the Internet across and nothing. Possibly I don't know what I am looking for. Here is the function:
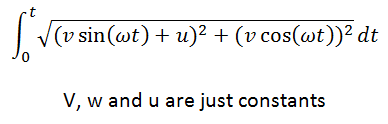
I can simplify it but it continues being difficult:
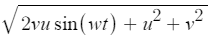
I can simplify it but it continues being difficult: