- #1
jamesb1
- 22
- 0
I am reviewing this http://deeplearning.cs.cmu.edu/pdfs/Cybenko.pdf on the approximating power of neural networks and I came across a definition that I could not quite understand. The definition reads:
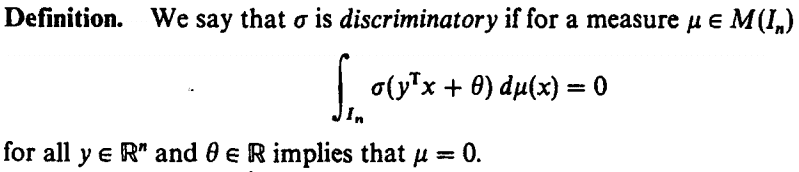
where $I_n$ is the n-dimensional unit hypercube and $M(I_n)$ is the space of finite, signed, regular Borel measures on In.
The only thing that I could get from this definition which again does not seem plausible enough is: since whenever the integral is 0 it must imply that the measure μ is 0, then σ is non-zero. I am not sure if this right though.
I literally could not find any other literature or similar definitions on this and I've looked in a number of textbooks such as Kreyzig, Rudin and Stein & Shakarchi.
Any insight/help?
where $I_n$ is the n-dimensional unit hypercube and $M(I_n)$ is the space of finite, signed, regular Borel measures on In.
The only thing that I could get from this definition which again does not seem plausible enough is: since whenever the integral is 0 it must imply that the measure μ is 0, then σ is non-zero. I am not sure if this right though.
I literally could not find any other literature or similar definitions on this and I've looked in a number of textbooks such as Kreyzig, Rudin and Stein & Shakarchi.
Any insight/help?
Last edited by a moderator: