- #1
FlipStyle1308
- 267
- 0
The three charges are held in place below. L = 1.40 m.
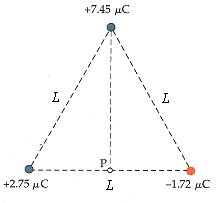
(a) Find the electric potential at point P.
(b) Suppose that a fourth charge, with a charge of 6.73 μC and a mass of 4.71 g, is released from rest at point P. What is the speed of the fourth charge when it has moved infinitely far away from the other three charges?
For part (a), I am pretty sure that I use the equation U = kqoq/r, but don't know what to do next.
(a) Find the electric potential at point P.
(b) Suppose that a fourth charge, with a charge of 6.73 μC and a mass of 4.71 g, is released from rest at point P. What is the speed of the fourth charge when it has moved infinitely far away from the other three charges?
For part (a), I am pretty sure that I use the equation U = kqoq/r, but don't know what to do next.