- #1
- 1,753
- 143
The table gives values of a continuous function. Use the Midpoint Rule to estimate the average value of f on [20, 50]
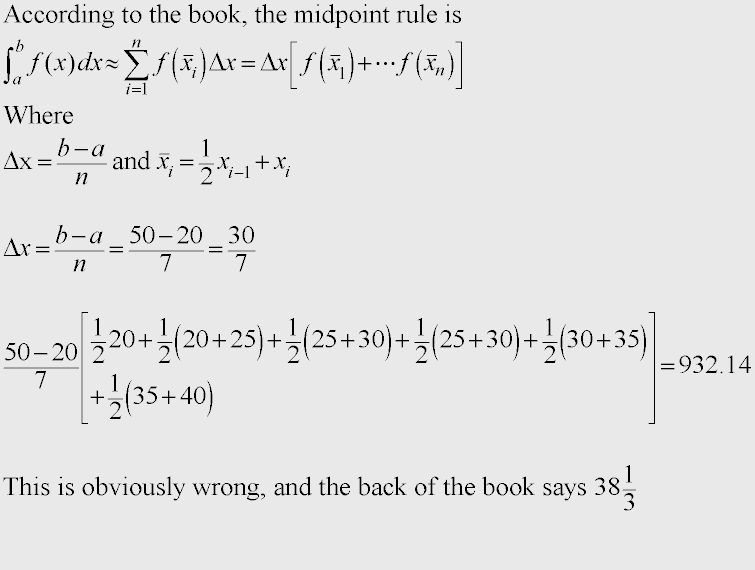
Code:
x 20 25 30 35 40 45 50
f(x) 42 38 31 29 35 48 60