- #1
pleasehelpme6
- 62
- 0
Electric Dipole Electric Field.. URGENT
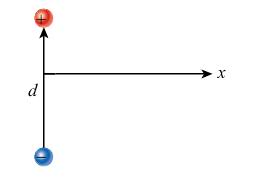
For the electric dipole shown in the figure, express the magnitude of the resulting electric field as a function of the perpendicular distance x from the center of the dipole axis in terms of the electric dipole moment, p.
E = Fq
P = qd
E = kq/(r^2)
R = sqrt[(d/2)^2 + x^2]
q = P/d
Thus,
E = kP/{d*[sqrt(d/2)^2+x^2]^2}
Since I'm looking for the x-component, multiply E by the cos(theta), which in this case is x/R, or...
cos(theta) = x/sqrt[(d/2)^2+x^2]
so the answer i get is...
E = kP/{d*[sqrt(d/2)^2+x^2]^2} * x/sqrt[(d/2)^2+x^2]
which comes out to be...
E = kP/[sqrt(d/2)^2+x^2]^(3/2) * x/d
The final answer is actually...
E = kP/[sqrt(d/2)^2+x^2]^(3/2)
So my question is, what happens to the x/d?
Homework Statement
For the electric dipole shown in the figure, express the magnitude of the resulting electric field as a function of the perpendicular distance x from the center of the dipole axis in terms of the electric dipole moment, p.
Homework Equations
E = Fq
P = qd
E = kq/(r^2)
The Attempt at a Solution
R = sqrt[(d/2)^2 + x^2]
q = P/d
Thus,
E = kP/{d*[sqrt(d/2)^2+x^2]^2}
Since I'm looking for the x-component, multiply E by the cos(theta), which in this case is x/R, or...
cos(theta) = x/sqrt[(d/2)^2+x^2]
so the answer i get is...
E = kP/{d*[sqrt(d/2)^2+x^2]^2} * x/sqrt[(d/2)^2+x^2]
which comes out to be...
E = kP/[sqrt(d/2)^2+x^2]^(3/2) * x/d
The final answer is actually...
E = kP/[sqrt(d/2)^2+x^2]^(3/2)
So my question is, what happens to the x/d?