Nebuchadnezza
- 78
- 2
Here is an interesting brainteaser I found. Looking at the earlier post with the circle and the tangent, I thought people here might be interested. I do have the answer to this riddle so this is not homework by any means.
The problem goes as follows
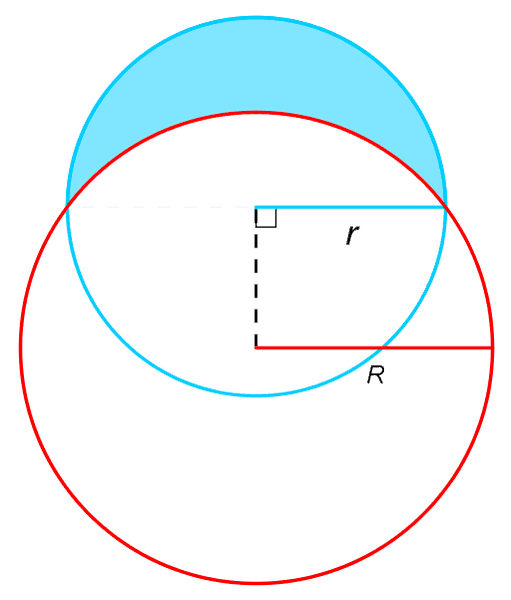
1) Find the area of the crescent-shaped region (called a lune)
bounded by arcs of circles with radii r and R.
2) What is the maximum area of the lune ?
The problem goes as follows
1) Find the area of the crescent-shaped region (called a lune)
bounded by arcs of circles with radii r and R.
2) What is the maximum area of the lune ?