How to analyse a rigid frame on wheels?

[kleptomaniac]

Hey Forum
I'm hoping someone can help me gain some clarify with this problem. This is related to the trolley design thread i created; however this is a different problem so i thought it best to start a new thread. Hope that's ok.

Basically, i want to analyze a basic rigid frame for a 4 wheel trolley to determine the internal member forces and perform the usual analysis to determine the ideal beam design and material.
Under normal operation, the operator will apply a horizontal push force (F = 225N) on the horizontal handles, which will move the trolley forwards.
I'm familiar with analyzing frames in static equilibrium as I've done plenty of these as homework before. However, because the trolley has 4 wheels, the frame reactions will be purely vertical (to balance the cargo load applied, W = 2943N, concentrated as L/2). Everything's fine as long as no external horizontal forces are introduced into the frame analysis.

If i introduce the push force in the FBD however (see image below), the frame will no longer be in static equilibrium, as there are no horizontal reaction forces to balance it out.

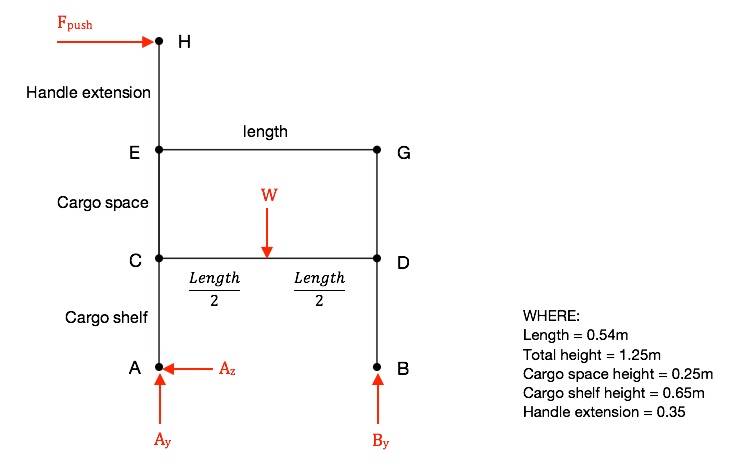
My initial approach was to lock the rear wheels so they act as a simple fixed supports; that way the rear wheels would be able to balance the horizontal push force (assuming the brakes are able to handle this force without slipping). However this has given me some inconsistencies in my analysis, with some of the internal forces being different depending on how i solved for them (which doesn't make sense). This leads me to think that maybe I'm going about it the wrong way (i'm fairly certain I'm not just doing bad math).

What would be the best way to perform a frame analysis for this type of wheeled problem? I thought i might be able to google how similar moving frames are analyzed (car and bike frames for example), however i wasn't able to find anything helpful.
Assuming the frame is moving horizontally doesn't seem right as I'd then have to deal with horizontal acceleration.
Alternatively i thought maybe just remove the wheels and analyze the frame with both A & B as simple fixed supports instead (with horizontal and vertical reactions). However I'm not sure if this would be the best approach either.

Any ideas would be appreciated.

 

[CWatters]

If i introduce the push force in the FBD however (see image below), the frame will no longer be in static equilibrium, as there are no horizontal reaction forces to balance it out.

Correct. If the horizontal forces don't sum to zero the trolley will accelerate. Since the trolley/load has mass there will be inertial forces on the cart/load that sum to equal the applied force. Depending on what you are doing you can either take the inertial loads to be a single force acting at the centre of mass, individual forces acting on each component of the trolley/loads, or somewhere in between (for example if the mass of the load is much greater than the trolley you might ignore the inertial load of the trolley and just account for the inertial of the load)..

For example the combination of the applied force on the handle and the inertial force of a load on the bottom shelf will cause a clockwise torque on the trolley increasing the load on the front wheels and reducing the load on the rear wheels.

However this only happens while the trolley is accelerating. Once up to constant velocity the inertial force disappears. A bigger problem might occur when the trolley hits an obstruction like a curb and stops very quickly. The inertial forces could in some cases be large enough to tip the trolley over.

 

[CWatters]

PS: If there are no horizontal forces (eg no rolling resistance, no air resistance etc) then the operator cannot apply a horizontal force on the handle without the trolley accelerating. At a constant velocity it takes no force to push the trolley.

 

[kleptomaniac]

For example the combination of the applied force on the handle and the inertial force of a load on the bottom shelf will cause a clockwise torque on the trolley increasing the load on the front wheels and reducing the load on the rear wheels.

Yup, that's pretty much what my initial frame analysis says. The front wheel reaction is significantly higher at 1992.33N, compared to the rear wheel 950.67N.
So this shouldn't be the case then if the trolley is stationary? So does that mean my analysis is wrong?
My assumption was that with the rear wheel brakes engaged, it would act as a regular simple support with horizontal and vertical reactions as on my FBD. However this relies entirely on the horizontal rear wheel reaction completely balancing the push force (with no sliding).

Here's the frame analysis calculations i did for the FBD i posted with the rear wheel's brakes engaged to prevent horizontal motion due to the push force:

---------------------------------------------------------------
Calculating the initial reactions for the full frame:

Disassembling the members to perform individual analysis:

---------------------------------------------------------------

I'm not sure if it makes sense that member 4 has vertical reactions as there's no load applied to it - unless the push handle moment is responsible for those vertical reactions at G & E.

Based on those calculations, I've already looked closer at member 3 since it has the load applied to it, and created a shear and moment diagram to determine the maximum bending stress etc and determined some suitable cross area dimensions for that beam. I still need to do the same for the main vertical supports (members 1 & 2), however I'm not sure if my calculated internal member forces are correct.
Like i said, I'm still not sure I'm analyzing the trolley the right way (as a static frame).

 

[kleptomaniac]

Would it make sense to analyze the frame from the frame of reference of the trolley itself? That is, when the operator is pushing the trolley, it will be moving forwards while everything else around it is standing still. However from the frame of reference of the trolley, it will actually be stationary (everything else is moving instead); so the push force will not be part of the FBD in that reference frame, with only vertical forces due to the weight of the load?
I guess for that to work, an assumption needs to be made that the trolley is moving at constant velocity, so its acceleration is 0.
That might be over simplifying it perhaps. My intuition tells me that the push force should really be analyzed as part of the system to ensure the frame member design is able to withstand the force.

 

[CWatters]

I haven't had time to work through all those calculations but..

Yup, that's pretty much what my initial frame analysis says. The front wheel reaction is significantly higher at 1992.33N, compared to the rear wheel 950.67N.
So this shouldn't be the case then if the trolley is stationary? So does that mean my analysis is wrong?

Not wrong just a different situation to the one I was describing. I've tried to sum up the two situations in a quick sketch below.

My assumption was that with the rear wheel brakes engaged, it would act as a regular simple support with horizontal and vertical reactions as on my FBD. However this relies entirely on the horizontal rear wheel reaction completely balancing the push force (with no sliding).

The various forces could be roughly similar in both cases if we make some assumptions...

a) In the accelerating case the centre of gravity is low as shown. If the centre of gravity was higher (say at the same level as the applied force) then there might be less (or no) clockwise moment under acceleration.

b) As you said, in the static case there must be sufficient friction force to prevent the wheels sliding. The clockwise moment alters the load on the wheels, reducing it at the rear wheel and increasing it at the front. The maximum friction force that can occur before the wheels slip depends on the load on the rear wheel and that reduces as the applied force increases. As a check the equation for the maximum friction force is..

F_f = μN

where μ is the coefficient of friction and N is the normal force (950N)

Rearrange to give

μ = F_f/N = 220/950 = 0.23

That's not a difficult value to achieve..
http://www.engineeringtoolbox.com/friction-coefficients-d_778.html
(scroll down to "Friction Coefficients for some Common Materials and Materials Combinations")

If the wheels start to slip then you have a combination of both situations. The horizontal forces won't sum to zero and the cart starts to accelerate. The sum will be something like Applied force + Kinetic Friction force + Inertial force (m*a) = 0.

If this is real world exercise then I think the horizontal forces will be highest when hitting an obstruction (rapid deceleration) or someone tries to shove the trolley thinking the brakes are off when they are still on.

 

[D.B.SriHridai]

You are saying that it's a frame. I don't know why you are looking to analyse in dynamic equilibrium. Though if you apply external load or force it moves the body. In order to get the acceleration acquired during this time then you need to consider dynamic equilibrium i.e. De' Alembert's principle. If you are interested to analyse know frame then consider static equilibrium inorder to know how much load it can with stand