Lorentz invariant integral measure

[DOTDO]

Hi

I'm studying electron-muon scattering

and now considering the Lorentz invariant integration measure.

The textbook introduced it, which use dirac delta function to show that d3p/E is a Lorentz scalar.

I understood it but I wanted to find other way and tried like this:

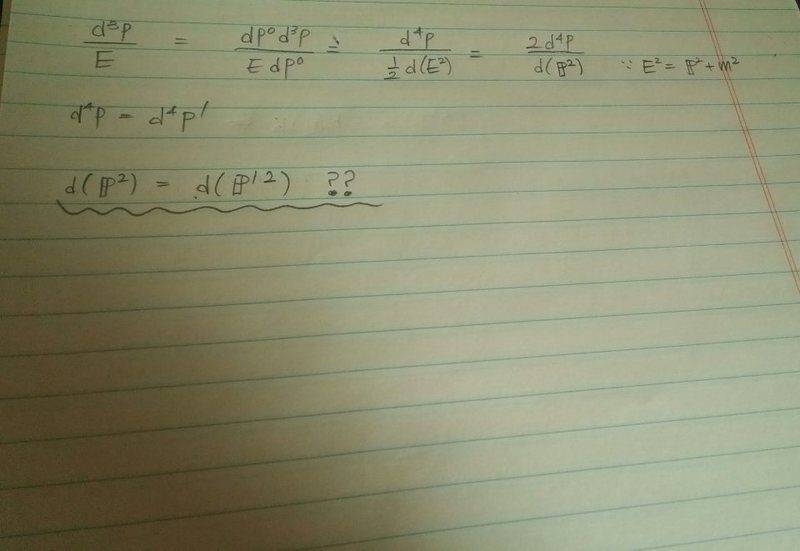
I need a hint on the underlined equation. The primed one is lorentz transformed one.

How can I show that d(p^2) is Lorentz invariant?

Just calculate it hard ?

 

[Demystifier]

Your attempt has a mistake because $E$ is not the same as $p^0$. The four variables $p^0,p^1,p^2,p^3\equiv (p^0,{\bf p})$ are 4 independent variables, but $E=\sqrt{{\bf p}^2+m^2}$ is not independent of ${\bf p}$. Hence, your conclusion that $d{\bf p}^2$ should be Lorentz invariant is wrong.

The measures $d^4p=dp^0 d^3p$ and $\frac{d^3p}{E}$ are Lorentz invariant, but $dE d^3p$ and $\frac{d^3p}{p^0}$ are not.

If you are still confused, try first to solve the following problem. Consider 3-dimensional Euclidean space with Cartesian coordinates $x,y,z$. In this space, consider the sphere defined by $x^2+y^2+z^2=R^2$, which is a 2-dimensional object invariant under 3-dimensional rotations. Find the measure of area $dA$ on the upper half of the sphere, in the form $dA=f(x,y)dxdy$. Argue that this measure is rotation-invariant simply because the sphere is rotation-invariant. Find $f(x,y)$ explicitly in two ways: (i) geometrically and (ii) by starting from volume element $dV=dxdydz$ and using a $\delta$-function trick. Can you see the relation with the problem of Lorentz-invariant measure above? In particular, can you see the analogy between $R$ and $m$?

Partial solution: You should get $$f(x,y)=\frac{R}{\sqrt{R^2-x^2-y^2}}.$$Is it correct to write the right-hand side as $R/z$?

 

[Demystifier]

(ii) by starting from volume element dV=dxdydz and using a δ-function trick.

Since I have nothing more important to do at the moment, let me do this explicitly. In spherical coordinates we have
$$dV=dA dr$$
where $dA$ is the area element of the sphere. Since $dr\delta(r-R)=1$, we can use this to write
$$dA=dV\, \delta(r-R). \;\;\; (1)$$
We also have
$$\delta(R^2-r^2)=\delta((R-r)(R+r))=\frac{\delta(R-r)}{2R}$$
so (1) can be written as
$$dA=dV \, 2R\delta(R^2-r^2) \;\;\; (2)$$
Clearly, (2) is rotation invariant. In Cartesian coordinates this can be written as
$$dA=dxdydz \, 2R\delta(R^2-x^2-y^2-z^2) \;\;\; (3)$$
Introducing the function
$$w(x,y)=\sqrt{R^2-x^2-y^2}$$
which is non-negative on the sphere of radius $R$, (3) can be written as
$$dA=dxdydz \, 2R\delta(w^2-z^2)=dxdydz \, 2R\delta((w-z)(w+z)) \;\;\; (4)$$
For the upper half of the sphere we have $z>0$, so for the upper half (4) can be written as
$$dA=dxdydz \, 2R \frac{\delta(w-z)}{2w}=dxdy \frac{R}{w}. \;\;\; (5)$$

Since this is rotation invariant and since $R$ is a constant, it follows that the measure
$$\frac{dxdy}{w}$$
is rotation invariant. This is analogous to the fact that the measure
$$\frac{d^3p}{\omega}$$
with $\omega=\sqrt{m^2+{\bf p}^2}$ is Lorentz invariant. The differences are that (i) for Lorentz invariance we have one dimension more, and (ii) some signs are different because Minkowski metric is different from the Euclid metric.

 

[vanhees71]

Isn't this a bit too complicated? Usually the derivation starts from the fact that $\mathrm{d}^4 p$ is invariant under proper Lorentz transformations. Then the on-shell $\delta$-distribution, $\delta(p^2-m^2)=\delta[(p^0)^2-E^2]$, where $E^2=\vec{p}^2+m^2$. Finally $\Theta(p^0)$ is a Lorentz invariant under proper orthochronous Lorentz transformations and thus finally
$$\mathrm{d}^4 p \Theta(p^0) \delta(p^2-m^2)=\mathrm{d} p^0 \mathrm{d}^3 \vec{p} \frac{1}{2E} \delta(p^0-E)$$
is Lorentz invariant. Thus if you have a function $f(p)$ with $p^0=E$ you can write
$$\int \mathrm{d}^4 p \Theta(p^0) \delta(p^2-m^2)=\int \mathrm{d}^3 \vec{p} \frac{1}{2E} f(p^0=E,\vec{p}).$$
If $f(p)=f(p^0,\vec{p})$ is a scalar field, then for the on-shell function $f(p^0=E,\vec{p})$ the 3D integral with the measure $\mathrm{d}^3 \vec{p}/E$ is a scalar.

 

[Demystifier]

Isn't this a bit too complicated?

Yes, but he already indicated that he understands the standard proof of Lorentz invariance with the use of a delta function. He wanted a more direct proof without a delta function, and in his attempt he failed. I wanted to explain him what exactly was wrong with his attempt. In addition, I also thought that it would be easier to undertstand this in a case which can be more easily visualized, i.e. where 4-dimensional Lorentz invariance is replaced with 3-dimensional rotational invariance. While the calculation turned out to be longer, I thought that the resulting geometric idea would be easier to understand intuitively.

 

[ShayanJ]

Your attempt has a mistake because E is not the same as $p^0$. The four variables $p^0,p^1,p^2,p^3\equiv (p^0,{\bf p})$ are 4 independent variables, but $E=\sqrt{{\bf p}^2+m^2}$ is not independent of p.

I don't understand this part.
1) The 4-momentum is always defined to be $p^\mu=(E,\bf p)$ in a particular frame. Now you say $p^0$ is not the same as E. So what is it?
2) You say that different components of the 4-momentum are independent but what about the restriction $p^2=-m^2$ on any 4-momentum?

 

[Demystifier]

I don't understand this part.
1) The 4-momentum is always defined to be $p^\mu=(E,\bf p)$ in a particular frame. Now you say $p^0$ is not the same as E. So what is it?
2) You say that different components of the 4-momentum are independent but what about the restriction $p^2=-m^2$ on any 4-momentum?

Since $E$ is defined as $\sqrt{{\bf p}^2+m^2}$, these two questions are really the same. To answer them, it should be enough to give one example where $p^{\mu}$ is not equal to $(E,\bf p)$. So here is one example: the 4-momentum integration in a Feynman diagram with a loop.

If you are still confused, think about doing the exercise proposed in #2.

 

[ShayanJ]

Since $E$ is defined as $\sqrt{{\bf p}^2+m^2}$, these two questions are really the same. To answer them, it should be enough to give one example where $p^{\mu}$ is not equal to $(E,\bf p)$. So here is one example: the 4-momentum integration in a Feynman diagram with a loop.

If you are still confused, think about doing the exercise proposed in #2.

I think I understand it now. It seems that the right way of thinking about 4-momentums is that there is a 4-dimensional momentum space and particles move on $p^2=-m^2$ hypersurfaces in this space. I was missing this viewpoint. thanks.