Moving Clock: Lorentz Factor Calculation

[Dimani4]

Hi guys!
I want to thank to all the guys which helping us to understand the beauty and mystery of the relativistic theory.
Here I just want to share the calculation of Lorenz factor for the moving clock in the frame of reference of the "stationary" observer. This time the clock is not perpendicular to the movement but parallel. Here is is.

Written: Time that observer sees (measures) when clock moving in v direction. I did clock with w length between two plates.

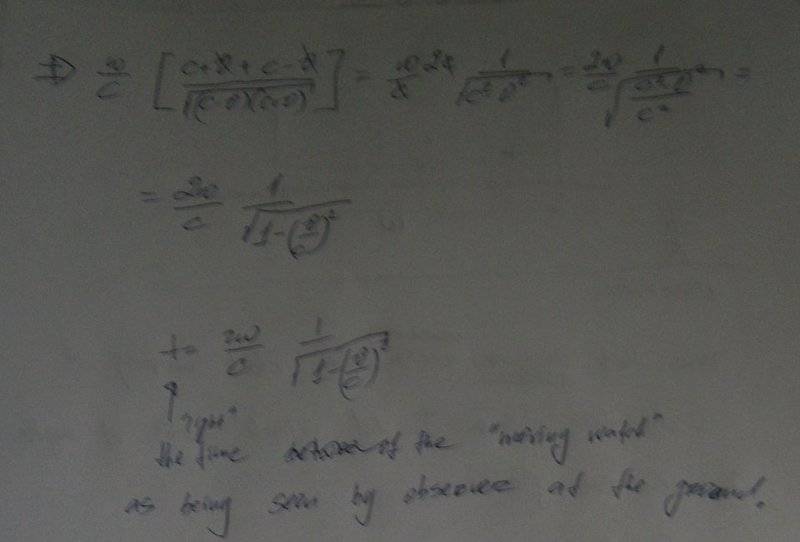In the end is written: "The "light" time of the moving watch as being seen by observer at the ground.
This time observer at the ground measures with his "ground" watch. Meaning, he will measure "more" time by the factor called Lorentz factor. Every second in his watch will be (sqrt(1-v^2/c^2)) sec in the moving watch.

Thank you.

 

[robphy]

It might be helpful to render this in $\LaTeX$.

This kind of light clock is called the
https://www.google.com/search?q="longitudinal+light-clock"
as opposed to the usual "transverse light-clock".
(You can see both clocks in my avatar... click on it to see the animated version.)

 

[jtbell]

Indeed, I strongly suggest you take a look at our LaTeX primer, if you haven't already:

https://www.physicsforums.com/help/latexhelp/

This method has two important advantages:

1. The equations look better (no problems with handwriting style or poor lighting)

2. Responders can quote individual equations by quoting the LaTeX code, which isn't possible if they're embedded in an image (JPEG, GIF, etc.).