- #1
jackcarroll434
- 11
- 5
Homework Statement: Calculate the power of heating source required in a heat exchanger
Relevant Equations: Heat transfer for LMTD heat exchanger.
I have a real-world problem whereby:
Water is flowing at a constant flow rate of 10 mL/min through a PVC tube, inner radius of 1.25mm and outer radius of 2mm, that is surrounded by an aluminium shell, inner radius of 2mm and outer radius of 4mm. The length of the tube is 0.2m. Water enters at a temperature of 20 degC and must exit at a temperature of 37 degC. The aluminium shell is heated by an external heat source with an unknown power rating, and the temperature of the aluminium is regulated by a temperature feedback loop (thermocouple). The outside environmental temperature is at room temperature. Determine the power of the heat source required.
I have made the following assumptions to simplify the problem:
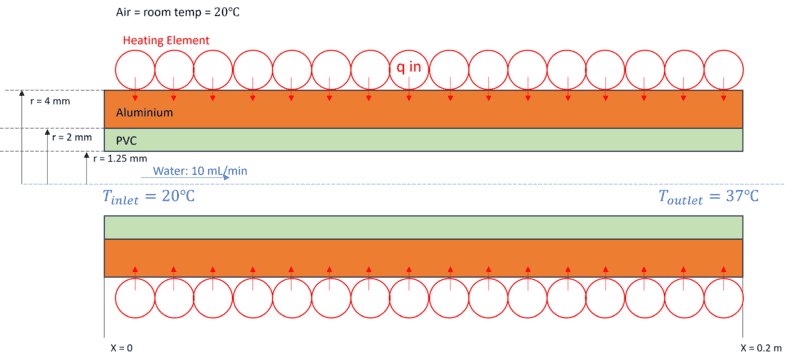
Which I have simplified with my above assumptions to:
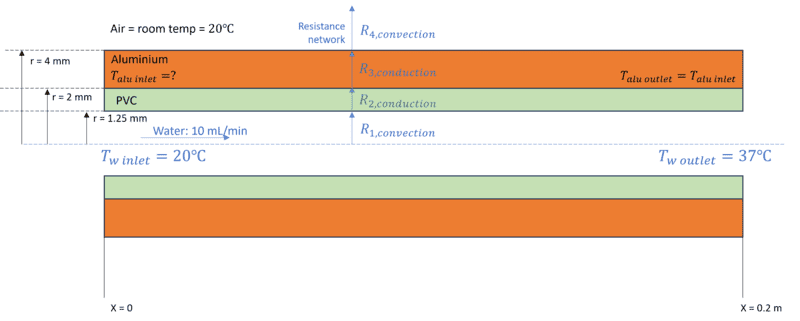
I approached this problem by assuming that it works similarly to a parallel flow heat exchanger, using the LMTD method as below:
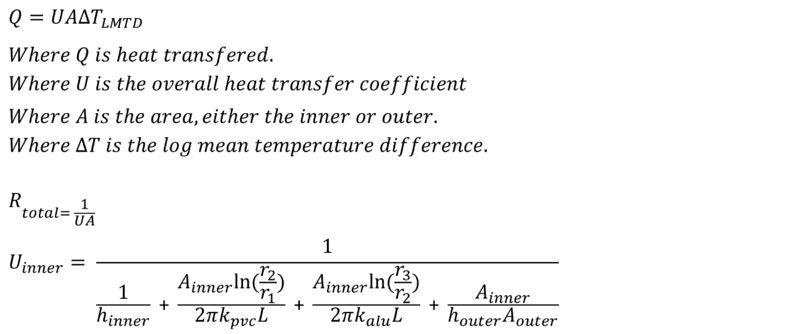
I then solved to find U:

Before finding the theoretical rate of energy transfer needed to raise the temperature of the flowing water:
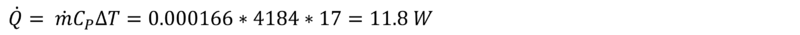
Knowing U, Q and A, I rearranged the LMTD heat transfer equation to solve for the temperature of the aluminium:
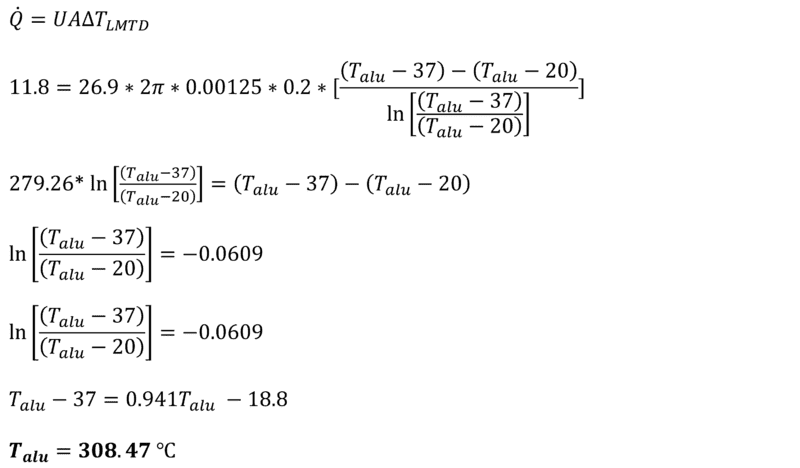
I would like to know:
Relevant Equations: Heat transfer for LMTD heat exchanger.
I have a real-world problem whereby:
Water is flowing at a constant flow rate of 10 mL/min through a PVC tube, inner radius of 1.25mm and outer radius of 2mm, that is surrounded by an aluminium shell, inner radius of 2mm and outer radius of 4mm. The length of the tube is 0.2m. Water enters at a temperature of 20 degC and must exit at a temperature of 37 degC. The aluminium shell is heated by an external heat source with an unknown power rating, and the temperature of the aluminium is regulated by a temperature feedback loop (thermocouple). The outside environmental temperature is at room temperature. Determine the power of the heat source required.
I have made the following assumptions to simplify the problem:
- The temperature of the aluminium can be assumed to remain constant, as the temperature feedback loop is designed to keep it a fixed temperature. Additionally, the thermal heat transfer and losses to the surroundings are considered to have negligible impact on the temperature of the aluminium.
- Heat transfer between the heat source and the aluminium can also be assumed to be 100% efficient (to simplify the problem).
Which I have simplified with my above assumptions to:
I approached this problem by assuming that it works similarly to a parallel flow heat exchanger, using the LMTD method as below:
I then solved to find U:
Before finding the theoretical rate of energy transfer needed to raise the temperature of the flowing water:
Knowing U, Q and A, I rearranged the LMTD heat transfer equation to solve for the temperature of the aluminium:
I would like to know:
- If this method for solving the problem is theoretically valid, or if you would have approached it another way.
- How you might go about determining the minimum power of the heater required to keep the aluminium at this temperature. This will need to balance the power supplied with losses to the environment and heating the fluid.