- #1
Memo
- 35
- 3
Poster reminded to always show their work when starting schoolwork threads
- Homework Statement
- Lim (x->0) (cosx-sqrt(cos2x))/tan^2(x)
x∈(-π/4;π/4)\{0}
- Relevant Equations
- lim (x->x0) (1-cosa*f(x))/[f(x)]^2=a^2/2
Can't attempt to solve the task.
I'd appreciate it a lot if you could help!
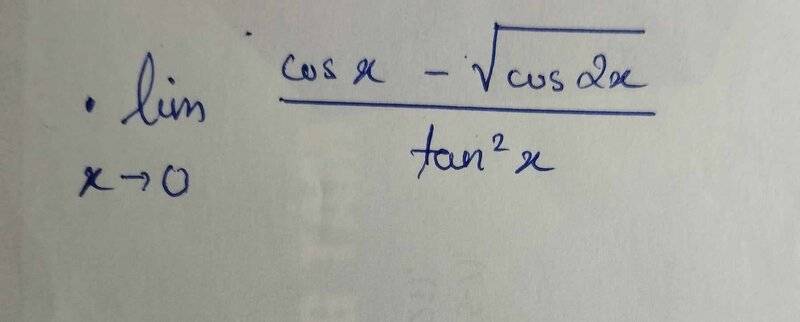
I'd appreciate it a lot if you could help!