What is the effect of curvature on the rigidity of a beam?

[pervect]

I didn't want to derail the last thread on the sliding block, but I think I noticed something interesting.

If we look at http://arxiv.org/abs/0708.2490v1

consider first the image in figure 3

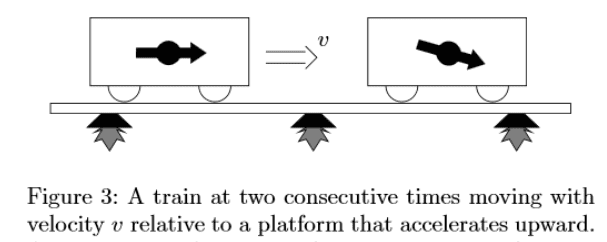
and compare it to the image

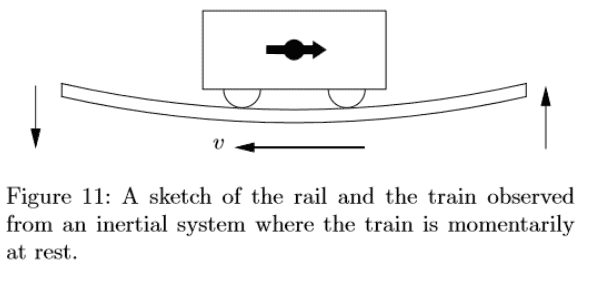
in figure 11.

Ignore the wheels, which complicate matters, for the time being, and assume the block actually slides directly on the floor. In the first image, the middle of the sliding block is flush with the floor of the elevator, in the second it is above the floor, and only the two ends of the block touch the floor.

So the two diagrams are not of the same physical situation as far as the shape of the train goes.

If we assume the situation is described as figure 3, then in figure 11 the trains belly should "sag" to match the floor. The train wouldn't be "flat" in an instantaneous comoving frame.

If we assume the situation is as described in figure 11, the drawing in figure 3 would have to change. The train would have to be bent in an upside-down U shape, in order for its middle to be above the floor.

This behavior does not seem Born rigid at all. But maybe it doesn't have to be...

1) If we imagine actually taking a flat block and pushing on one end to slowly accelerate it horizontally across the floor of the elevator, which figure represents the physical situation when we are done? (I think it should be figure 11, with the train flat in its own frame, and in the elevator frame with the belly of the train raised above the floor of the elevator).

This leads to 2

2) We note that the train is rotating relative to a gyroscope after it's accelerated, where it was previously not rotating relative to a gyroscope before its acceleration. This suggest to me that the motion described above ("gentle horizontal acceleration") isn't a Born rigid motion, even though at first glance it appears to be linear.

 

[pervect]

add: It looks like I need to review Matas' paper, http://arxiv.org/abs/gr-qc/0305106, "Relativistic Arquimedes law for fast moving bodies and the general-relativistic resolution of the “submarine paradox". He does some detailed calculations of how the shape of what I call a block (and what he calls a submarine) evolves. From a quick re-reading the easiest approach appears to be to assume the block is very thin, then use the "no expansion" condition. But the deatils are messy enough I'm not quite sure what he says the answer actually is yet as to the shape of the block, or if he's really solving the same problem I'm interested in.

 

[WannabeNewton]

If we assume the situation is described as figure 3, then in figure 11 the trains belly should "sag" to match the floor. The train wouldn't be "flat" in an instantaneous comoving frame.

Allow me to quote something I said from the other thread:

If we do as the article says and go to a momentary rest frame of the platform and then boost to the momentary rest frame of the train on the platform at this instant then in this frame the platform actually looks parabolic due to relativity of simultaneity-a very simple Lorentz transformation calculation verifies this explicitly. Since the platform+train system is stationary (no time dependence) this should obviously be the case no matter what momentary rest frame of the platform we choose and so we can conclude that in the rest frame of the train, the platform is a backwards moving parabolic shape. This will of course make the gyroscope precess relative to the train frame in a clockwise manner since the parabola is convex.

So just for clarity, if I'm understanding you correctly, are you applying the exact same argument to the base of the train, seeing as how the base of the train itself has a component of motion in uniform linear acceleration upwards, ergo it too would appear as a convex parabola in its own rest frame while appearing straight/flat in the momentary rest frame of the platform?

 

[pervect]

Allow me to quote something I said from the other thread:

If we do as the article says and go to a momentary rest frame of the platform and then boost to the momentary rest frame of the train on the platform at this instant then in this frame the platform actually looks parabolic due to relativity of simultaneity-a very simple Lorentz transformation calculation verifies this explicitly. Since the platform+train system is stationary (no time dependence) this should obviously be the case no matter what momentary rest frame of the platform we choose and so we can conclude that in the rest frame of the train, the platform is a backwards moving parabolic shape. This will of course make the gyroscope precess relative to the train frame in a clockwise manner since the parabola is convex.

So just for clarity, if I'm understanding you correctly, are you applying the exact same argument to the base of the train, seeing as how the base of the train itself has a component of motion in uniform linear acceleration upwards, ergo it too would appear as a convex parabola in its own rest frame while appearing straight/flat in the momentary rest frame of the platform?

I'm not sure the argument is exactly the same. Let me try to clarify the argument by considering only one case for clarity, a case where a block is sliding along the elevator floor, and every point of the bottom block is in contact with the floor, the block is resting on the floor with no gaps.

Then when we perform the transformation you describe (which I've also done), the floor is parabolic shaped according to a point inertial observer instantaneously comoving with the block.

If the bottom of the block is in contact with the floor along the whole length of the block , then logically the block must also be parabolic shaped on its bottom according to the same point observer.

This implies that the case we've considered, a case where we have a block sliding on a flat floor everywhere touching the floor, we must have the block warped in "it's own rest frame", by which I mean the frame of an inertial observer instantaneously co-moving with the block.

OK so far? If so, then I'll get on to the rest of the issue, which gets more complex.

 

[WannabeNewton]

So we've imposed the frame invariant constraint that every point of the bottom of the block must remain in contact with the floor right? Then yes OK so far, do continue! :)

 

[pervect]

OK. Now, for the real problem. We start out with a flat block on the elevator floor, and we start to accelerate it gradually in the x direction (while the elevator continues to accelerate in the z direction).

We want to do this as rigidly as possible.

Our motivational question is: what does the block look like when this is done? We eventually want both perspectives, the "block" perspective and the "floor" perspective. From the "block" perspective we can ask - does the block stay in contact everywhere with the floor (and hence bend) as in the scenario above, or does the block stay straight in a comoving frame (in which case the center of the block lifts up off the floor). Or does perhaps something else happen?

I'd also like to know what it looks like from the "floor" perspective, though I'm phrasing the question from the "block" perspective.

First question: can we use the notion of a Born rigid motion of the block to solve this problem, or does (as I suspect) the rotation of the block relative to a gyroscope nix this idea.

Second question: If we can't use Born rigid motion, what tools do we use to solve the problem? Matas seems to suggest that we can use only the "expansion free" part of the Born rigidity condition, but I'm not sure I'm following him corretly.

 

[pervect]

Matas seems to say that the submarine / block "experiences shear in the transition region" - this is mentioned on page 2 of http://arxiv.org/pdf/gr-qc/0305106v1.pdf - so apparently the motion of the block is, as I suspected, not Born rigid.

Matas talks about some eigenvalues (right after eq 7) but I can't make heads or tails of what he's doing there :(.

By my count, if we simplify the problem by relying on the symmetry in y, we have three components of the four velocity - dt/dtau, dx/dtau, and dz/dtau as variables in the equation for the evolution of the block shape. For constraints we have that the normalization condition of the four velocity, and the zero expansion condition. So we are short one constraint to determine the differential equations which control evolution of the shape of the block in the transition region.

 

[WannabeNewton]

Matas seems to say that the submarine / block "experiences shear in the transition region" - this is mentioned on page 2 of http://arxiv.org/pdf/gr-qc/0305106v1.pdf - so apparently the motion of the block is, as I suspected, not Born rigid.

Right and note we can make sense of this using the usual intuition about Born rigid rotation. If the block is accelerating uniformly upwards and at the same time moving to the right at constant speed then it follows an orbit of a circulating time-like Killing field and so describes Born rigid rotation. As we know if we take an object at rest and through some acceleration phase put it into a state of Born rigid rotation then the acceleration phase itself will not be Born rigid.

Matas talks about some eigenvalues (right after eq 7) but I can't make heads or tails of what he's doing there :(.

The deformation rate of the submarine due to shear stress along the principal axes of the shear tensor are given by the eigenvalues of the shear tensor. All Matas is doing is calculating the eigenvalues of the shear tensor for the 4-velocity field (3) and stating various conditions of minimization of the eigenvalues (and thus of the deformation rate of the submarine) so as to keep minimal the shear stresses on the submarine. All this is during the acceleration phase of course. However I'm not sure why Matas discusses the minimization of the eigenvalues of the shear tensor as he/she doesn't seem to make use of such a minimization anywhere else in the paper. I suppose it's just as a precautionary measure in order to avoid unnecessary complications/"paradoxes" that may arise in the problem as a result of a significant shear tensor resulting in a significant deviation from Born rigidity.

By my count, if we simplify the problem by relying on the symmetry in y, we have three components of the four velocity - dt/dtau, dx/dtau, and dz/dtau as variables in the equation for the evolution of the block shape. For constraints we have that the normalization condition of the four velocity, and the zero expansion condition. So we are short one constraint to determine the differential equations which control evolution of the shape of the block in the transition region.

What kind of acceleration profile are you applying to the block? Do you have an explicit analytic form for the 3-velocity of the block relative to the floor in mind? Clearly the upwards acceleration is just that of the accelerating floor (or equivalently that of a uniform gravitational field) but you would still have to specify the acceleration profile in the direction along the floor. Matas for example has the 3-velocity relative to the fluid given by (4). If this profile is given one can straightforwardly write down a 4-velocity for the block and perform computations of kinematical quantities in an attempt to analyze the desired properties of the block in its instantaneous rest frames during the acceleration phase and afterwards when it has settled into a constant rightwards drift speed (while still accelerating upwards along with the floor).

 

[pervect]

The deformation rate of the submarine due to shear stress along the principal axes of the shear tensor are given by the eigenvalues of the shear tensor.
All Matas is doing is calculating the eigenvalues of the shear tensor for the 4-velocity field (3) and stating various conditions of minimization of the eigenvalues (and thus of the deformation rate of the submarine) so as to keep minimal the shear stresses on the submarine. All this is during the acceleration phase of course. However I'm not sure why Matas discusses the minimization of the eigenvalues of the shear tensor as he/she doesn't seem to make use of such a minimization anywhere else in the paper. I suppose it's just as a precautionary measure in order to avoid unnecessary complications/"paradoxes" that may arise in the problem as a result of a significant shear tensor resulting in a significant deviation from Born rigidity.

Thanks, I couldn't make heads or tails of this part - I still don't follow the details, but it appears I don't have to. Do you know if Wald or MTW go into any details of this, or would I have to go to some other text for a review of the significance of the eigenvalues of the shear tensor?

What kind of acceleration profile are you applying to the block? Do you have an explicit analytic form for the 3-velocity of the block relative to the floor in mind? Clearly the upwards acceleration is just that of the accelerating floor (or equivalently that of a uniform gravitational field) but you would still have to specify the acceleration profile in the direction along the floor. Matas for example has the 3-velocity relative to the fluid given by (4). If this profile is given one can straightforwardly write down a 4-velocity for the block and perform computations of kinematical quantities in an attempt to analyze the desired properties of the block in its instantaneous rest frames during the acceleration phase and afterwards when it has settled into a constant rightwards drift speed (while still accelerating upwards along with the floor).

I was hoping for insight from Matas on the details of the acceleration profile. That was why I wanted to review the paper. Re-reading it, I think I've found the missing condition that allowed Matas to compute the trajectories from the no-expansion condition.

Hence, a generic submarine point will have a timelike trajectory in the region
x > 0, given by Z = $Z_0$ = const, y = $y_0$ = const and ...

So Matas assumes dZ/dT = 0, and dZ/dtau = (dZ/dT) (dT/dtau), so he's essentially assuming in coordinate independent terms that the comonent of the 4-velocity dZ/dtau = 0, which seems reasonable at first glance - but I have reservations. It seems to me that this is equivalent to assuming that the bottom of the block remains in contact with the floor.

Specifically, the elevator floor is defined by Z=0, and if we consider any point on the block starting at Z=0, it remains at Z=0, which means it remains on the elevator floor.

But how do we reconcile this with his other statement:

It is interesting to notice that although mariners aboard will not perceive any significant change in the submarine’s form, observers at rest with the fluid will witness a relevant contraction in the x-axis direction as a function of Z (and $v_0$); indeed, more at the top than at the bottom (

I think that having the floor become a parabola rather than straight would be a "significant change in the submarine's form" that would be "noticed by the mariners aboard".

Given that we agree that the elevator floor becomes a parabola, and that having the bottom of the submarine touch the floor implies that the block does as well, then the submarine does undergo a significant change in shape (it appears bent in its own frame) when undergoing the trajectory that Matas computes.

Unless I've missed something, but so far I don't see anything I"ve missed.

[add]
I did miss something, the word "significant". Perhaps the resolution is that the change in shape isn't "significant". It would be worth considering this issue more.

It seems that to answer my question, I'd have to drop the no-expansion condition in favor of writing a Lagrangian for the block (perhaps the hyperelastic one), specifying as a constraint the motion (or perhaps the forces) on one side of the block, then computing the answer. Unfortunately this is a lot more work than I'm willing to attempt.

[add]
I might not have to go this far, actually - the point is that the block has a Lagrangian, and the Lagrangian has no memory (actual materials might creep and suchlike, but the Lagrangian isn't that sophisticated).

If we know the shape that minimizes the Lagrangian in its start frame, the similarity between the start frame and the end frame suggests that we know the shape in the end frame.

 

[WannabeNewton]

Do you know if Wald or MTW go into any details of this, or would I have to go to some other text for a review of the significance of the eigenvalues of the shear tensor?

Wald only mentions it in passing and MTW doesn't seem to mention it at all. I'll try to find more detailed sources but for now check out section 2.2 of http://www.physics.uoguelph.ca/~poisson/research/agr.pdf and section 2.8 of http://www.socsci.uci.edu/~dmalamen/bio/GR.pdf specifically p.173.

Specifically, the elevator floor is defined by Z=0, and if we consider any point on the block starting at Z=0, it remains at Z=0, which means it remains on the elevator floor.

I agree with that.

I think that having the floor become a parabola rather than straight would be a "significant change in the submarine's form" that would be "noticed by the mariners aboard".

Given that we agree that the elevator floor becomes a parabola, and that having the bottom of the submarine touch the floor implies that the block does as well, then the submarine does undergo a significant change in shape (it appears bent in its own frame) when undergoing the trajectory that Matas computes.

I have a couple of points to make. Firstly, I think that the phrase "significant change in the submarine's form" is ambiguous as to its intent. Possibly Matas means to say that there is no significant structural change in the submarine's form due to shear stresses since we've minimized the eigenvalues of the shear tensor. This would be a different kind of "change in shape" when compared to for example the floor appearing flat in its own instantaneous rest frame whilst appearing parabolic in the instantaneous rest frame of the submarine because the former refers to a measurable structural change in shape effected by tangential forces induced by the shear stresses whereas the latter refers to change in shape due to the relativity of simultaneity. The reason I say the phrasing is ambiguous is he subsequently refers to the Lorentz contraction of the submarine relative to the fluid as an example of a "change in shape" of the submarine relative to the fluid but this is a change in shape in the latter sense of relativity of simultaneity and not in the former sense of physical shear stresses.

This brings me to my second point. Consider for simplicity the submarine as drifting to the right with constant speed $v$ at a constant altitude $z = \frac{1}{g}$ in a downwards uniform gravitational field of magnitude $g$, where $v$ is relative to the observers at rest in the gravitational field. The points of the submarine would be described by the tangent field $\xi^{\mu} = (1,v,0,0)$ in Rindler coordinates. Then we know that $\xi_{[\gamma}\partial_{\mu}\xi_{\nu]}\neq 0$ because the vorticity of $\xi^{\mu}$ is in fact given by $\omega^{\mu} = \epsilon^{\mu\nu\alpha\beta}\xi_{\nu}\partial_{\alpha}\xi_{\beta}= (0,0,vg,0)$.

In light of this, it's clear that we (or at least I) have been using the term "instantaneous rest frame" of the submarine in a rather cursory manner: since $\xi_{[\gamma}\partial_{\mu}\xi_{\nu]}\neq 0$ there is no common global simultaneity surface amongst the observers comoving with different points of the submarine and hence no single notion of the "shape of the submarine" relative to the submarine in the simultaneity sense again because there is no single global simultaneity surface shared by the observers comoving with different points of the submarine, assuming of course that we're attempting to use local Einstein (radar) simultaneity. So to be more careful and precise we should probably qualify the "shape" of the submarine as being relative to the instantaneous rest frame of a specific point of the submarine. However which point we choose shouldn't make a difference regarding the "shape" of the submarine or the shape of the floor because all points of the submarine have the same constant rightwards speed during the drift phase relative to the floor.

 

[pervect]

I've more or less convinced myself that for any normal material, if we imagine a uniformly loaded beam supported at both ends of the parabolic shaped floor, the expected mechanical sag due to gravity will be greater than the sag in the floor, hence the beam/block/train/submarine will remain in contact with the floor. (For clarity I should pick one of beam, block, train, and submarine and stick with it, but it's easier to note that I'm talking about the same thing by different names.)

Rather than go through all the details, I'll just give the end answers, if anyone is interested enough to check that I haven't made an error it will be a plus:

First, the sag in the floor.

Letting a be the acceleration of the elevator in the frame in which the floor is flat, let g = $\gamma^2 a$ be the proper acceleration of the block (the local gravity), and L be the proper length of the block.

I then get the sag (from end to middle) to be

$$\frac{1}{2} g \Delta t^2 = \frac{1}{2} g \left( \frac{\beta L}{2c} \right)^2$$

$\Delta t$ is the change in coordinate time between the middle and end of the block in the elevator frame, which is assumed to be small compared to c/g.

For a uniformly loaded beam supported at both end, with a bulk modulus of K and a poisson's ratio of zero, of length L, height h, density $\rho$, and base width b:

$$\frac{5 \cdot 12}{384 \cdot 3} \frac{\rho}{K} g \frac{L^4}{h^2}$$

The speed of sound in the material should be about $\sqrt{K/\rho}$ which will be << c
b does not appear in the end result.

The Young's modulus E was computed from K and poisson's ratio, the value of zero for the later was chosen for my convenience.

As long as L > 2h, even for a material where the speed of sound is c, the sag due to gravity loading for a beam (block) supported at both ends should be more than the sag in the floor. The formulas used for the beam sag are standard Newtonian ones, and I"m not sure how accurate they are if the beam is as tall or taller than it is long, nor how accurate they are for hypothetical materials stiff enough to have the speed of sound approach "c", since I looked them up without considering how they were derived

 

[pervect]

Somehow my last post vanished :(

I have a couple of points to make. Firstly, I think that the phrase "significant change in the submarine's form" is ambiguous as to its intent.

I quite agree.

This brings me to my second point. Consider for simplicity the submarine as drifting to the right with constant speed $v$ at a constant altitude $z = \frac{1}{g}$ in a downwards uniform gravitational field of magnitude $g$, where $v$ is relative to the observers at rest in the gravitational field. The points of the submarine would be described by the tangent field $\xi^{\mu} = (1,v,0,0)$ in Rindler coordinates. Then we know that $\xi_{[\gamma}\partial_{\mu}\xi_{\nu]}\neq 0$ because the vorticity of $\xi^{\mu}$ is in fact given by $\omega^{\mu} = \epsilon^{\mu\nu\alpha\beta}\xi_{\nu}\partial_{\alpha}\xi_{\beta}= (0,0,vg,0)$.

Conclusive proof that the submarine is rotating, I think, and it emphasises why you can't accelerate it from its initial unmoving state to its final moving state in a Born rigid manner.

In light of this, it's clear that we (or at least I) have been using the term "instantaneous rest frame" of the submarine in a rather cursory manner:

Hmmm - me too, I'll have to ponder this a bit more, but at the moment I don't think it's too much of an omission.

 

[AlephZero]

For a uniformly loaded beam supported at both end, with a bulk modulus of K and a poisson's ratio of zero, of length L, height h, density $\rho$, and base width b:

$$\frac{5 \cdot 12}{384 \cdot 3} \frac{\rho}{K} g \frac{L^4}{h^2}$$

The speed of sound in the material should be about $\sqrt{K/\rho}$ which will be << c
b does not appear in the end result.

The Young's modulus E was computed from K and poisson's ratio, the value of zero for the later was chosen for my convenience.

As long as L > 2h, even for a material where the speed of sound is c, the sag due to gravity loading for a beam (block) supported at both ends should be more than the sag in the floor. The formulas used for the beam sag are standard Newtonian ones, and I"m not sure how accurate they are if the beam is as tall or taller than it is long, nor how accurate they are for hypothetical materials stiff enough to have the speed of sound approach "c", since I looked them up without considering how they were derived

The "speed of sound" is irrelevant - in classical mechanics, this is being treated as a statics problem (in the appropriate reference frame!) not a dynamics problem.

The basic assumption is that the curvature of the beam is small, or alternatively the length of the curved center line of the beam is the same as the initial length, to first order.

The other main assumption is that plane sections of the beam remain plane and perpendicular to the center line. A more careful analysis for a given shape of cross section (i.e. continuum mechanics imposing the correct boundary conditions) shows that plane sections do not remain plane but typically warp into an "S" shape through the depth of the beam, and the "best fit" plane through the warped section is not perpendicular to the center line. From an engineering point of view, these errors are negligible (a few percent at most) if the length / depth of the beam > 10.

For shorter beams, the next biggest effect is that the material deforms in shear, so that all the cross sections tend to stay in the vertical plane rather than being normal to the curved center line. You should be able to find a formula for that correction, if you look for "deep beams" and/or "shear factors". Your uncorrected formula under-estimates the deflections.

If Poisson's ratio is non-zero, there is also so-called anticlastic curvature effect. Poisson's ratio causes the sides of the beam are pushed apart on the compression side of the curve and pulled together on the tension side, and the top and bottom surfaces form a curve that makes a saddle-point with the curvature along the length of the beam. (You can demonstrate this easily by bending a block of rubber, e.g. a pencil eraser.)

But whether any of this matters to your relativistic arguments is way over my head!

 

[pervect]

The "speed of sound" is irrelevant - in classical mechanics, this is being treated as a statics problem (in the appropriate reference frame!) not a dynamics problem.

The ratio $K / \rho$ appears in the equation, $\rho$ being the density and K being the bulk modulus. This can be recognized as the square of the speed of sound (compression waves) in the material, see http://en.wikipedia.org/wiki/Speed_of_sound#Equations. I find expressing the ratio as the speed of sound makes the equations more physically meaningful for me. A high speed of sound makes for a "stiffer" structural material, and "c" serves as an obvious upper bound for just how rigid something can be.

http://www.islandone.org/LEOBiblio/SPBI1MA.HTM also uses this idea, though they use Y instead of K, I'm not sure offhand which is more accurate.

The basic assumption is that the curvature of the beam is small, or alternatively the length of the curved center line of the beam is the same as the initial length, to first order.

The other main assumption is that plane sections of the beam remain plane and perpendicular to the center line. A more careful analysis for a given shape of cross section (i.e. continuum mechanics imposing the correct boundary conditions) shows that plane sections do not remain plane but typically warp into an "S" shape through the depth of the beam, and the "best fit" plane through the warped section is not perpendicular to the center line. From an engineering point of view, these errors are negligible (a few percent at most) if the length / depth of the beam > 10.

For shorter beams, the next biggest effect is that the material deforms in shear, so that all the cross sections tend to stay in the vertical plane rather than being normal to the curved center line. You should be able to find a formula for that correction, if you look for "deep beams" and/or "shear factors". Your uncorrected formula under-estimates the deflections.

I find this sort of encouraging. It seems a bit unreasonable that you could prevent the bottom of the beam from sagging by piling enough stuff on top of it, I rather expected the equations I used were not suited to "short" beams.