- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading James Munkres' book, Elements of Algebraic Topology.
Theorem 6.3 on page 37 concerns the homology groups of the Klein Bottle.
Theorem 6.3 demonstrates that the homology groups for the Klein Bottle are as follows:
[itex] H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2 [/itex]
and
[itex] H_2 (S) = 0 [/itex]
I need some help following a key part of the proof.
The relevant section of the proof is as follows:
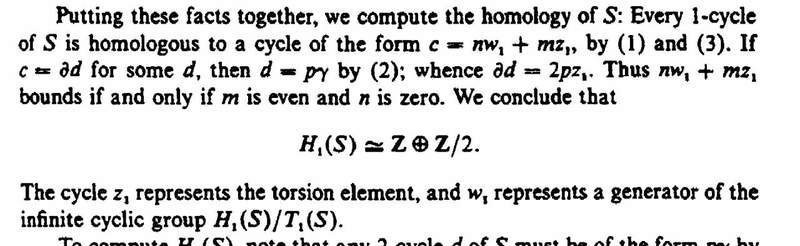
(To provide context to this post, the full theorem and proof is given at the end of this post - see below)
My understanding of the above part of Munkres' proof is as follows:
Munkres establishes that a cycles in S are of the form
[itex] c = n w_1 + m z_1 [/itex]
so that [itex] Z_1 (S) = \mathbb{Z} \oplus \mathbb{Z} [/itex]
Munkres also establishes that boundaries are of the form
[itex] c = (2p) z_1 [/itex]
so that [itex] B_1 (S) = 2 \mathbb{Z} [/itex]
Thus, so far as I can see we then have:
[itex] H_1 (S) = Z_1(S) / B_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/ 2 \mathbb{Z} [/itex]
BUT ... how does this tally with Munkres expression
[itex] H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2 [/itex]?
Indeed what does [itex] \mathbb{Z} \oplus \mathbb{Z}/2 [/itex] mean?
(I am not even sure whether the expression is
[itex] H_1 (S) = ( \mathbb{Z} \oplus \mathbb{Z}) /2 [/itex]
or
[itex] H_1 (S) = \mathbb{Z} \oplus (\mathbb{Z}/2) [/itex]
Hope someone can help.
The full text of Theorem 6.3 and its proof are as follows:

Hope someone can help.
Peter
Theorem 6.3 on page 37 concerns the homology groups of the Klein Bottle.
Theorem 6.3 demonstrates that the homology groups for the Klein Bottle are as follows:
[itex] H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2 [/itex]
and
[itex] H_2 (S) = 0 [/itex]
I need some help following a key part of the proof.
The relevant section of the proof is as follows:
(To provide context to this post, the full theorem and proof is given at the end of this post - see below)
My understanding of the above part of Munkres' proof is as follows:
Munkres establishes that a cycles in S are of the form
[itex] c = n w_1 + m z_1 [/itex]
so that [itex] Z_1 (S) = \mathbb{Z} \oplus \mathbb{Z} [/itex]
Munkres also establishes that boundaries are of the form
[itex] c = (2p) z_1 [/itex]
so that [itex] B_1 (S) = 2 \mathbb{Z} [/itex]
Thus, so far as I can see we then have:
[itex] H_1 (S) = Z_1(S) / B_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/ 2 \mathbb{Z} [/itex]
BUT ... how does this tally with Munkres expression
[itex] H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2 [/itex]?
Indeed what does [itex] \mathbb{Z} \oplus \mathbb{Z}/2 [/itex] mean?
(I am not even sure whether the expression is
[itex] H_1 (S) = ( \mathbb{Z} \oplus \mathbb{Z}) /2 [/itex]
or
[itex] H_1 (S) = \mathbb{Z} \oplus (\mathbb{Z}/2) [/itex]
Hope someone can help.
The full text of Theorem 6.3 and its proof are as follows:
Hope someone can help.
Peter
Attachments
Last edited:
