- #1
zenterix
- 541
- 75
- Homework Statement
- Prove the following theorem (Axler, Linear Algebra Done Right, Theorem 3.109)
Suppose ##V## and ##W## are finite-dimensional and ##T\in L(V,W)##. Then
(a) ##\text{dim range}\ T' = \text{dim range}\ T##
(b) ##\text{range}\ T'=(\text{null}\ T)^0##
- Relevant Equations
- (a)
##\text{dim null}\ T' = \text{dim null}\ T + \text{dim}\ W-\text{dim}\ V\tag{1}##
##=\text{dim} W'-\text{dim range}\ T'\tag{2}##
##=\text{dim}\ W-\text{dim range}\ T'\tag{3}##
From (1) and (3) we have
##\text{dim range}\ T'=\text{dim}\ V-\text{dim null}\ T=\text{dim range}\ T\tag{4}##
My question is about item (b).
(b)
Here is what I drew up to try to visualize the result to be proved
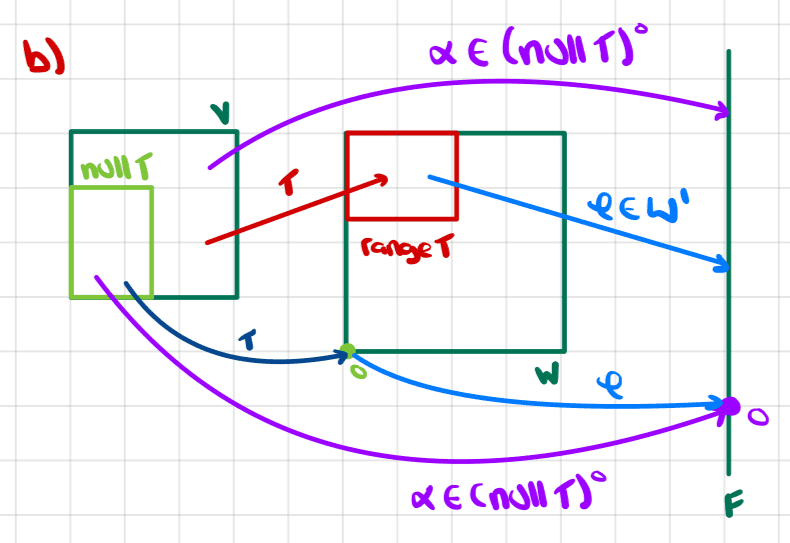
The general idea, I think, is that
1) ##(\text{null}\ T)^0## and ##\text{range}\ T'## are both subspaces of ##V'=L(V,\mathbb{F})##.
2) We can show that they have the same dimension.
3)We can show that ##\text{range}\ T' \subseteq (\text{null}\ T)^0##
4) From (2) and (3) we can prove that the two subspaces are in fact the same subspace.
Honestly, I did steps (1)-(3) myself and was looking for a way to infer (4) but didn't realize that I could use (2) and (3) to do so, so I looked at the proof in the book.
I'd like to know if there is another way to infer (4).
Here is what I have
##(\text{null}\ T)^0## is by definition all the linear functionals in ##V'## that map ##\text{null}\ T## to 0 in ##\mathbb{F}##.
For every ##\varphi\in W'##, the linear functional ##\varphi\circ T## maps ##\text{null}\ T## to 0 in ##\mathbb{F}##, so ##\varphi\circ T## is in ##(\text{null}\ T)^0##.
Now, at this point, it could be that there are other elements in ##(\text{null}\ T)^0## that are not one of the ##\varphi\circ T##.
How can I prove that this is not possible (in an alternative manner to (4))?
(b)
Here is what I drew up to try to visualize the result to be proved
The general idea, I think, is that
1) ##(\text{null}\ T)^0## and ##\text{range}\ T'## are both subspaces of ##V'=L(V,\mathbb{F})##.
2) We can show that they have the same dimension.
3)We can show that ##\text{range}\ T' \subseteq (\text{null}\ T)^0##
4) From (2) and (3) we can prove that the two subspaces are in fact the same subspace.
Honestly, I did steps (1)-(3) myself and was looking for a way to infer (4) but didn't realize that I could use (2) and (3) to do so, so I looked at the proof in the book.
I'd like to know if there is another way to infer (4).
Here is what I have
##(\text{null}\ T)^0## is by definition all the linear functionals in ##V'## that map ##\text{null}\ T## to 0 in ##\mathbb{F}##.
For every ##\varphi\in W'##, the linear functional ##\varphi\circ T## maps ##\text{null}\ T## to 0 in ##\mathbb{F}##, so ##\varphi\circ T## is in ##(\text{null}\ T)^0##.
Now, at this point, it could be that there are other elements in ##(\text{null}\ T)^0## that are not one of the ##\varphi\circ T##.
How can I prove that this is not possible (in an alternative manner to (4))?
Last edited: