- #1
ChiralSuperfields
- 1,316
- 141
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,

The solution is,
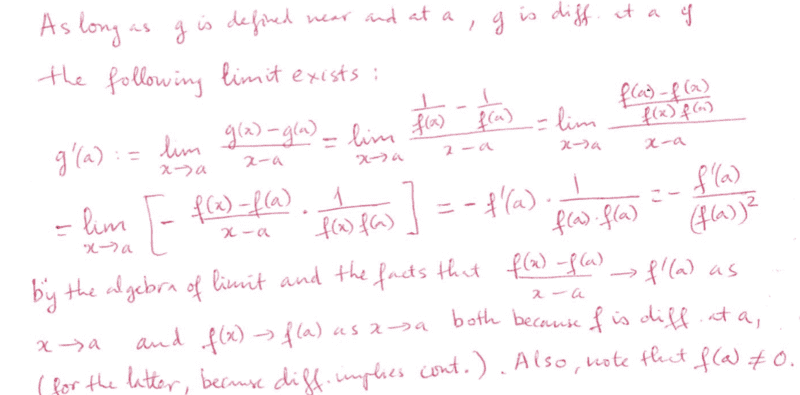
However, does someone please know why we allowed to assume that the derivative exists for f i.e ##f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}##?
Thanks!
The solution is,
However, does someone please know why we allowed to assume that the derivative exists for f i.e ##f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}##?
Thanks!