A Lesson In Teaching Physics: You Can’t Give It Away

A central principle of Physics Forums regarding homework help is not to provide solutions on demand but to guide students along a path to the answer.  The rationale behind this principle is articulated in the familiar saying, “If you give a hungry man a fish, you feed him for a day; if you teach him how to fish, you feed him for a lifetime.”  That said, I will quote another familiar saying, “You can lead a horse to water, but you can’t make him drink.”  Then I will blend the two into “You can teach a hungry man how to fish and lead him to the water, but you can’t make him fish.”

This mélange epitomizes a conclusion I reached after decades of teaching minds, some hungry some not, how to think. How I reached this conclusion and how I eventually came to terms with it are the subject of this article.

The seeds

When I began graduate school, my duties included helping with grading hourly exams in large classes (150-200 students).  Here is the exam question that started it all.

An electron of charge $-e$ enters with velocity $v$ a region of uniform magnetic field $B$ directed into the page.  It exits at a right angle from its original direction (see figure). Find the work that the magnetic force does on the electron from entry to exit.

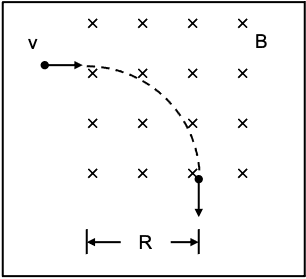
(A) $~evB\dfrac{\pi R}{2}$

(B) $~-evB\dfrac{\pi R}{2}$

(C) $~evB\sqrt{2}R$

(D) $~$  Zero.

 

Surprisingly few students, maybe a handful or two, gave the correct answer (D).  Most students chose (A) or (B) consistently with the dreaded generalization “work is force times distance.” I was astonished because the professor in charge of the course had a sterling teaching reputation. Surely, he must have taught it right.

Several years later, as a postdoc, I volunteered to team-teach a course on Modern Physics to gain demonstrable teaching experience before applying for a “real” job.  The course was split into two 30-student sections with a common syllabus set by my teammate professor. The details of implementing the syllabus for my section were left up to me and included authoring the hourly tests.

Shortly before the winter holiday break, I gave a scheduled short hourly test.  My instructions were “Select any two (emphasis in the original) of the following three statements, answer “True” or “False” and  justify your answer.”  To make sure they got it, I read aloud the instructions before handing out the questions.  The first statement was related to the Bohr model and the second to Compton scattering.

The third statement was “It is fun to ride on a one-horse open sleigh.”  It was my holiday gift to the class and I awarded full credit for all answers and justifications.  Still, about 1/3 of the students declined my offer and worked on the first two questions.  One of them told me that she answered the first two questions “just in case” because she didn’t believe I meant it.  I saw an element of distrust stemming, perhaps, from an ingrained perception that students and instructors are adversaries.  I was chagrined with the result and never contemplated “gifts” of this kind again.

The germination of an idea

Fast forward a decade. In my “real” job as a university assistant professor, my turn came to teach calculus-based introductory E&M to a large class.  When we got to “Motion of Charged Particles in Magnetic Fields,” I took extra care to point out that the Lorentz force is always perpendicular to the velocity and, therefore, to the path, that it does no work and that kinetic energy is conserved.  For good measure, I showed how the work-energy theorem fits in. Finally, I concluded with “and if someone asks you to find the work done by the magnetic force on the charged particle, don’t be fooled.  The only correct answer is zero.”  As the reader might have guessed, I had decided at that time to be the “someone”  and put the question on the final exam.

Upon grading the finals, I was distressed to see that only about a quarter of the answers were correct.  I went to see David, a veteran of the trench wars against ignorance, who was my unofficial mentor. I explained what happened and vented my frustration: but I told them!  He said, “Telling them is meaningless to a lot of students.” Then he related a story of his own.  After a dismal performance of his students on a homework problem in his Intermediate Mechanics class, he announced that he would put the same problem on the final. Well, you guessed it, only a handful of his students studied the problem and improved their performance. He concluded his story by saying, “Even if you tell them, there will always be some who won’t believe you.”  Flashback to the student who rejected my holiday gift.

Nevertheless, I stubbornly discounted David’s advice.  When “Motion of Charged Particles in Magnetic Fields” came around the next year, I was prepared.  I started with the presentation from the year before.  However, since that alone didn’t work, I worked out the question on the board and explained why the answer was (D).  Then I brazenly told them. I said, “I explained all this to last year’s class, but only a quarter got it right on the final.  Don’t be like them.  If you see this again, remember that uniform magnetic fields do zero work.”  I remember my voice wavering because part of me was wondering whether I was giving away too much.

Judgment day came and went with minimal improvement. The fraction of correct answers rose from one-quarter to one-third.  I went back to David with my second but I told them account.  He listened silently with a “and I told you” smirk on his face.

If you can’t beat them, join them

Chastened by the experience, I became convinced that telling them is necessary to teach but not reach students.  Leading them to the fountain of knowledge is not a guarantee that they will drink.  That was my “aha” moment.  Since it is difficult to give away even one question, I reasoned, why not give all of them away? Thus, the booklet came into being.

The booklet

The booklet was a compendium of about 120 homework-style but non-textbook problems from material covered throughout the course. I published it on the web for all to see.  On the first day of classes, I announced that each of the three hourly exams plus the final will consist of randomly selected problems from the booklet.  No tricks, no gimmicks, no guessing, no hidden traps.  All problems had numerical variables with numerical answers so that students could check and verify their work. However, questions on exams will appear with the numbers removed.  Students will have to derive the answers in symbolic form and show their derivations.  The booklet sections that would be fair game for each exam and my office hours for providing help were included.  The Appendix shows two sample problems from sections “Coulomb’s Law” and “Particles, Magnetic Fields & Currents”.

How did it work?

In theory

Ideally, a student will attempt all the problems appropriate to a particular exam before the event. The attempts should be concurrent with the related homework to allow sufficient time for asking questions.  I also encouraged the formation of study groups in which the students could work together and help each other.  I figured that maybe the horses that don’t want to drink might learn from those that do.  Also, by removing the numbers in the exam version, I hoped that students would abstract and remember a strategic and conceptual approach for each problem and bring that to the exam.

I was not worried that I gave too much away for two reasons: (a) David taught me that it’s not possible to give too much away; (b) in my mind, any student, who is able to reproduce the algebraic solutions to carefully crafted problems, has accomplished the goals of the course. I couldn’t expect more.

In practice

First the bad news.  Student traffic in my office was the same relative to the pre-booklet days. Only the focus of the visits changed from helping with difficult homework problems to helping with booklet problems.  Some students waited until the last moment and then crammed.  Others played the lottery and studied only the problems they guessed I would put on the test.  They didn’t believe me that the selection would be random.  Some felt that since they “knew” what would be on the exam, they could wing it without working out the problems.  In short,  the introduction of the booklet did not noticeably influence student habits or their performance on exams.  One might think that all of them would jump at the opportunity of knowing what would be on the exam. Not so.  Motivated horses drank, unmotivated ones did not.

Now for the good news.  The booklet turned out to be a win-win situation. For the students, it mitigated the fear and mental paralysis that afflict a lot of students before and during exams. An oft-heard lament was, “I thought I understood the material, I did all the homework, but when I came to the exam I freaked out.” With the booklet, the anxiety-producing unknowns, e.g. level of difficulty, the nature of the questions, where one ought to concentrate one’s efforts, whether one has sufficient preparation, etc. became known.  The booklet placed the responsibility of the student’s performance squarely upon themselves to where it belongs.

As a result, the booklet’s benefit to me was peace of mind. It removed the excuses that students use to shift the responsibility for their poor performance away from themselves: “The exam problems were nothing like the homework”; “We didn’t cover this in class”; “I didn’t understand this when we covered it in class”; “the exam was too tricky”; “the exam was too hard”; “you didn’t teach us how to solve this kind of problem” and so on.

However, the real winners were the motivated students (about 20%) who took the booklet to heart.  For them, it worked as I intended.  They treated the booklet problems as self-assigned homework. They came to office hours with questions every week often as teams working together.

The booklet also worked wonders with students who did poorly but cared enough to come and ask me how they could improve their performance. Most of them were last-minute crammers with poor time-management skills. For them, I constructed timetables to organize what to complete by what date and left it up to them. The next significant group consisted of students with shaky math or physics problem-solving skills. For them, I added a second set of timetables with to-learn lists.

Regardless of ability, all motivated students realized I did not design exams to expose their ignorance but to consolidate their learning. That was a big win for them and me.

Crafting the booklet

The booklet problems have no more than two sequential steps in the derivation and are not multipart problems.  Each question brings together concepts or skills that students should have acquired in some other part of the course or course prerequisites. Once solved numerically, the construction of the questions makes the transition from numerical to symbolic form transparent.  Furthermore, the questions do not require more than two sequential steps and the solution strategies are one-liners.

For example, questions 1.6 and 1.7, which cannot appear together on the same exam, combine electrostatics and free body diagrams. The strategy in both is “Draw an FBD for the top (or bottom) bead” and say that the net force on the chosen bead is zero.”  The trick (if there is one) is to realize that, even though the top bead is free to move, the string has to support the weight of both beads.

In question 6.5 the strategy is to “Express the magnitude of each wire’s contribution to the B-field in terms of the radius of the circle and the appropriate trig functions and set the two magnitudes equal.”  The question brings together the magnetic field of an infinite wire, superposition, and the right-hand rule. It also requires one to remember the identity $\sin(a\pm b)=\sin a\cos b\pm\cos a \sin b.$

Afterthoughts

The customary understanding between instructor and students is, “I am going to teach you and then I will examine you to determine what you have learned and what you can do.”  That’s OK in principle, however, there is often a gap separating the end of teaching from the beginning of learning. When students perform poorly, instructors tend to blame the students for not learning and students tend to blame the instructors for not teaching.  Nonetheless, both sides claim to have done their best.

This gap became painfully apparent to me with the electron-in-a-magnetic field question which I now regret asking.  It was a repeated measurement of what 2/3 (at best) of the students cannot do, not what they can do.   There is no information in finding out what students cannot do, instructors already know it.  The booklet shrunk the gap between teaching and learning.  It defined a boundary between the two with a clear message: “Here is what I expect you to be able to do. Let’s both see how well you can do it.  If there is something that you cannot understand or do, ask me before you are tested.”  To fish or not to fish, that is the question.

Appendix

In multipart booklet questions, such as the ones below, each part is standalone and does not require solving another part first. As far as the random number generator is concerned, each numbered part is a separate question, but questions sharing a descriptive statement do not appear together on the same exam, e.g. 1.6 or 1.7 but never 1.6 and 1.7.  Variables on the exam do not have numerical values; their symbols are left in place for students to use as given quantities.