Why Can’t My Computer Do Simple Arithmetic?

The first computer I owned was an Apple IIe computer, with a CPU that ran at slightly over 1 Megahertz (MHz), and with 64 Kilobytes (KB) of RAM, together with two 5 1/4″ floppy drives that could each store 140 Kilobytes (KB) of data.

My current computer (which costs about the same as the Apple computer) is vastly more powerful. It has a CPU that runs each of its four cores at 3.40 Gigahertz (GHz), 10 Gigabytes (GB) of RAM, and two hard drives with a total capacity of 1.5 Terabytes (TB). The increases in CPU clock speed, RAM size, and disk storage represent many orders of magnitude compared to my old Apple.

Even though the computer I have now is light years ahead of my first computer, it cannot do some pretty simple arithmetic, such as adding a few decimal fractions. Or maybe I should say, that the usual programming tools that are available aren’t up to this simple task. The following example is a program written in C, that adds 1/10 to itself for a total of ten terms. In other words, it carries out this addition: 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10  (ten terms). You might think that the program should arrive at a final value of 1, but that’s not what happens. In this Insights article, I’ll explain why the sum shown above doesn’t result in 1.

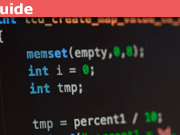
#include<stdio.h>

int main()
{
   float a = .1;
   float b = .25; // Not used, but will be discussed later
   float c = 0.0;
	
   for (int i = 0; i < 10; i++)
   {
      c += a;
   }
   printf("c = %.14f\n", c);
   
   return 0;
}

Here’s a brief explanation of this code, if you’re not familiar with C. Inside the main() function, three variables — a, b, and c — are declared as float  (four-byte floating point) numbers and are initialized to the values shown. The for loop runs 10 times, each time adding 0.1 to an accumulator variable c, which starts off initialized to zero. In the first iteration, c is reset to 0.1, in the second iteration it is reset to 0.2, and so on for ten iterations. The printf function displays some formatted output, including the final value of c.

The C code shown above produces the following output.

c = 1.00000011920929

People who are new to computer programming are usually surprised by this output, which they believe should turn out to be exactly 1. Instead, what we see is a number that is slightly larger than 1, by .00000011920929.  The reason for this discrepancy can be explained by understanding how many programming languages store real numbers in a computer’s memory.

How floating-point numbers are stored in memory

Compiler vendors for most modern programming languages adhere to the IEEE-754 standard for floating-point arithmetic (IEEE floating point). For float numbers in C or C++ or REAL  or REAL(4)  numbers (four-byte floating-point numbers), the standard specifies one bit for the sign, eight bits for the exponent, and 23 bits for the mantissa. This representation is similar to scientific notation (for example, as in Avogadro’s Number, $6.022 × 10^{23}$), except that the base is 2 instead of 10. This means that the decimal (base-10) number 1.5 would be stored in the form of something like $1.1_2 × 2^0$.

Here the exponent (on 2) is 0, and the mantissa is $1.1_2$, with the subscript 2 indicating this is a binary fraction, not a decimal fraction. The places to the right of the “binary” point represent the number of halves, fourths, eighths, sixteenths, and so on, so $1.1_2$ means 1 + 1(1/2), or 1.5.

One wrinkle I haven’t mentioned yet is that the exponent is not stored as-is; it is stored “biased by 127.” That is, 127 is added to the exponent that is stored. When you retrieve the value that represents the exponent, you have to “unbias” it by subtracting 127 from it to get the actual exponent.

The last point we need to take into account is that, with few exceptions, “binary” fractions are stored in a normalized form — as 1.xxx…, where each x following the “binary” point represents either a 0 bit or a 1 bit. Since these numbers all start with a 1 digit to the left of the “binary” point, the IEEE standard doesn’t bother to store this number.

The IEEE 754 standard for 32-bit floating-point numbers groups the 32 bits as follows, with bits numbered from 31 (most significant bit) down to 0 (least significant bit), left to right. The standard also specifies how 64-bit numbers are stored, as well.

SEEE EEEE EMMM MMMM MMMM MMMM MMMM MMMM

The bits have the following meanings:

• S – bit 31 – sign bit (0 for positive, 1 for negative)
• E – bits 30 through 23 – exponent bits (biased by 127)
• M – bits 22 through 0 – mantissa

Since there are only 23 bits for the mantissa (or 24 if you count the implied bit for normalization), we’re going to run into trouble in either of these cases:

• The mantissa contains a bit pattern that repeats endlessly.
• The mantissa doesn’t terminate within the available 23 bits.

Some floating-point numbers have exact representations in memory…

If you think back to when you first learned about decimal fractions, you might remember that some fractions have nice decimal forms, such as 1/5 being equal to 0.2 and 3/4 is equal to 0.75. Other fractions have decimal forms that are repeated endlessly, such as 1/3 = .333…, and 5/6 = 0.8333… The same is true for numbers stored as binary fractions, with some numbers having terminating representations, others having groups of digits that repeat, and still others with no terminating or repeating pattern.

The program at the beginning of this article had the following variable definition that wasn’t used. My reason for including this variable was to be able to find the internal representation of 0.25.

float b = .25;

It turns out that .25 is one of the floating-point numbers whose representation in memory is exact. If you notice that .25 is $0 × \frac 1 2 + 1 × \frac 1 4$, then as a binary fraction this would be $.01_2$. Subscript 2 is to emphasize that this is a base-2 fraction, not a decimal fraction.

In quasi-scientific notation, this would be $.01 × 2^0$, but this is not in the normalized form with a leading digit of 1. If we move the “binary” point one place to the right, making the mantissa larger by a factor of 2, we have to counter this by decreasing the exponent by 1, to get $.1 × 2^{-1}$. Moving the binary point one more place to the right gets us this normalized representation: $1.0 × 2^{-2}$.

This is almost how the number is stored in memory.

When I wrote the program that is presented above, I used the debugger to examine the memory where the value .25 was stored. Here is what I found: 3E 80 00 00 (Note: The four bytes were actually in the reverse order, as 00 00 80 3E.)

The four bytes shown above are in hexadecimal, or base-16. Hexadecimal, or “hex” is very easy to convert to or from base-2. Each hex digit represents four binary bits. In the number above, $3 = 0011_2$, $E = 1101_2$, and $8 = 1000_2$.

If I rewrite 3E 80 00 00  as a pattern of 32 bits, I get this:

0011  1111  0000  0000 0000  0000  0000  0000

• The red bit at the left is the sign bit, 0 for a positive number, and 1 for a negative number.
• The 8 blue bits are the biased exponent, $7D_{16}$, or $125_{10}$. If we unbias this (by subtracting 127), we get -2.
• The 23 orange bits on the right are the mantissa, all zero bits in this case. Remember that there is an implied 1 digit that isn’t shown, so the mantissa, in this case, is $1.000 … 0$.

This work shows us that 3E 80 00 00  is the representation in memory of $+1.0 × 2^{-2}$, which is the same as .25. For both the decimal representation (0.25) and the binary representation ($+1.0 × 2^{-2}$), the mantissa terminates, which means that 0.25 is stored in the exact form in memory.

… But other floating-point numbers have inexact representations

One such value whose representation isn’t exact is 0.1. When I looked for the representation in memory of 0.1, I found this four-byte hexadecimal number:

3D CC CC CD

Here’s the same number, written as a 32-bit bit pattern:

0011  1101  1100  1100  1100  1100  1100  1101

• The red bit at the left is the sign bit, 0 for a positive number, and 1 for a negative number.
• The 8 blue bits are the biased exponent, $7B_{16}$, or $123_{10}$. If we unbias this (by subtracting 127), we get -4.
• The 23 orange bits on the right are the mantissa. Dividing the mantissa into groups of four bits, and tacking an extra 0 bit to the right to make a complete hex digit, the mantissa is 1001 1001 1001 1001 1001 1010, which can be interpreted as the hexadecimal fraction $1.99999A_{16}$. (The leading 1 digit is implied.) It’s worth noting that the true bit pattern for 0.1 should have a mantissa of 1001 1001 1001 1001 1001 …, repeating endlessly. But because the infinitely long and repeating bit pattern won’t fit in the available 23 bits, there is some rounding that takes place in the last group of digits.

$1.99999A_{16}$ means $1 + \frac 9 {16^1} + \frac 9 {16^2} + \frac 9 {16^3} + \frac 9 {16^4} + \frac 9 {16^5} + \frac {10} {16^6}$ =1.6000000238418500000, a result I got using a spreadsheet.

Putting together the sign, exponent, and mantissa, we get we see that the representation of 0.1 in memory is $+1.6000000238418500000 × 2^{-4}$, or 0.100000001490, truncated at the 12th decimal place.

Conclusion

So…. to summarize what went wrong with my program, what I thought I was adding (0.1) and what was being added (0.100000001490) weren’t the same numbers. Instead of getting a nice round 1 for my answer, what I got was a little larger than 1.

We can minimize this problem to some extent by using 64-bit floating-point types (by declaring variables of type double in C and C++ and of type DOUBLE PRECISION  or REAL(8)  in Fortran), but doing so doesn’t eliminate the problem pointed out in this article.

Some programming languages, including Python and the .NET Framework, provide a Decimal type that yields correct arithmetic for a broad range of values. Any programmer whose application performs financial calculations that must be precise down to the cents place should be aware of the shortcomings of standard floating-point types, and consider using external libraries or built-in types, if available, that handle decimal numbers correctly.