A Geometrical View of Time Dilation and the Twin Paradox
Based on the number of questions we receive on the topic at Physics Forums, there is a lot of confusion in the general public about how time dilation works and the resolution of the twin paradox. More often than not, the confusion is based upon misunderstandings about how time dilation works and an unawareness of the relativity of simultaneity and how time is treated within special relativity. The aim of this Insight is to make an attempt at explaining these issues from a geometrical viewpoint and to see that we have an analogous effect in the geometry which we are used to, although we do not find it strange.
Table of Contents
A geometrical analogue
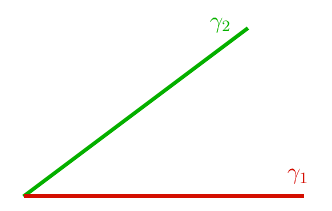
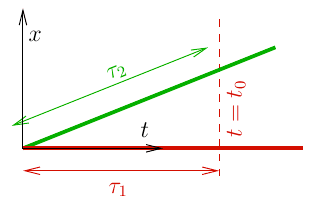
Consider the following two lines in normal two-dimensional space:
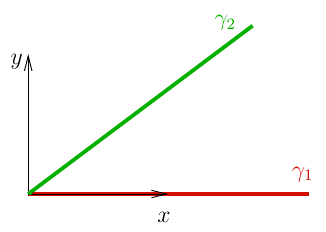
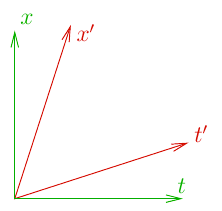
In order to describe the lines, we can introduce a coordinate system ##S##:
In this coordinate system, we may use the coordinate ##x## to parametrise the lines, we find that
$$y_1(x) = 0, \quad y_2(x) = kx,$$
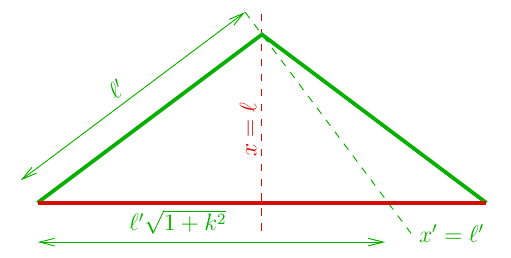
where ##k## is some constant. The lengths of each line between ##x = 0## and ##x = x_0## are simply given by Pythagoras’ theorem ##\ell^2 = \Delta x^2 + \Delta y^2## and we find
$$\ell_1 = x_0, \quad \ell_2 = x_0\sqrt{1+k^2}.$$
Consequently we find that the ratio between these two lengths is ##\ell_2/\ell_1 = \sqrt{1+k^2}##. This is shown in the following figure:
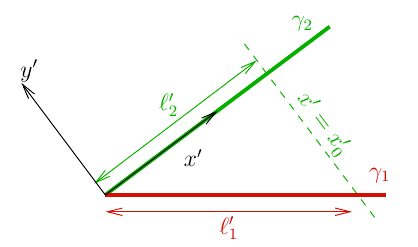
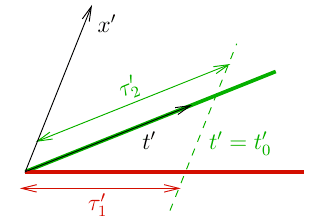
However, there is nothing special about the coordinate system ##S##. In particular, the length of the lines between any two given points on the lines does not depend on the coordinate system chosen and we could just as well have chosen to introduce the coordinate system ##S’## according to:
In this new coordinate system, we can parametrise the lines using the ##x’## coordinate
$$y_1′(x’) = -kx’, \quad y_2′(x’) = 0.$$
For the distance between the points corresponding to ##x’ = 0## and ##x’=x_0’##, Pythagoras’ theorem now results in
$$\ell_1′ = x_0′ \sqrt{1+k^2}, \quad \ell_2′ = x_0’$$
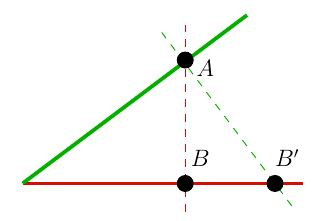
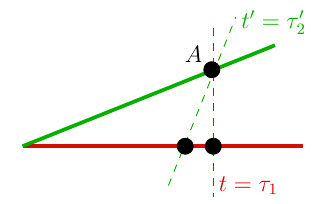
and so the line ##\gamma_1## is longer than ##\gamma_2## for the same difference in the parameter ##x_0’##, unlike in the case when the lines were parametrised by ##x##, where we obtained the opposite result. Yet there is nothing strange going on here. If we select a point on ##\gamma_2## and draw the lines which have the same ##x## and ##x’## values as that point, it becomes clear that the points on ##\gamma_1## which share the same parameter value differs depending on whether we used ##x## or ##x’## for the parametrisation. We should therefore not be surprised to find that the length to these two different points is different. Let us call this effect the “relativity of the same ##x##-coordinate”. Naturally, this effect does not affect the actual length of any of the lines, but only what lengths are being compared. This is illustrated in the following figure:
The points ##B## and ##B’## have the same ##x## and ##x’## coordinate as ##A##, respectively, yet correspond to different points on the curve ##\gamma_1## and therefore the distance from the intersection along this curve is different.
Curves intersecting at two points
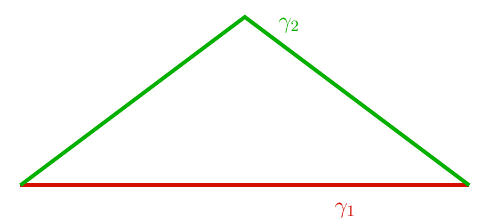
Now consider the following two curves:
Just from the figure, it should be clear that ##\gamma_2## is longer and we can verify this by introducing the coordinate system ##S## as above and computing the lengths of each of the curves, with the length of ##\gamma_2## being split into two equal contributions, one from each line segment.
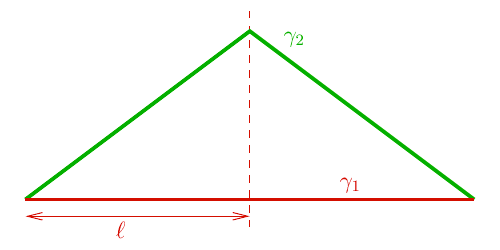
We find that
$$\ell_1 = 2\ell, \quad \ell_2 = 2\ell \sqrt{1+k^2}.$$
We could also compute the length of the curves by looking at the ##S’## coordinate system:
By our previous discussion, the length of ##\gamma_2## up to the half-way point is given by
$$\ell_2’/2 = \ell’,$$
while the length of ##\gamma_1## to the same ##x’## coordinate is given by
$$\ell_1’/2 = \ell’ \sqrt{1+k^2}.$$
If we were not careful about the relativity of the same ##x##-coordinate, we might do the error of thinking that ##\ell_1’/2## would be half the length of the curve ##\gamma_1##. However, since we are aware of this, we know better than that and realise that if we multiplied the result by two, we would obtain a result that was too large.
Application to relativity
So how does this connect to relativity and time dilation? In its foundation, relativity is a theory about the geometry of space-time, which may be described using a coordinate system with four coordinates ##(t,x,y,z)##, where the first coordinate is the time coordinate and the last three are spatial coordinates. It is important to realise that, just as in the case we just described, these are just coordinated that, by themselves, do not have a direct physical interpretation. For the sake of brevity, let us consider only one spatial coordinate ##x## as the generalisation is straightforward.
In relativistic space-time, geometry works a bit differently as compared to the geometry with which we are used to working with. In particular, this manifests itself by a change in Pythagoras’ theorem, which now comes with a minus sign
$$c^2 \tau^2 = c^2 \Delta t^2 – \Delta x^2$$
as a direct consequence of the speed of light is equal in all frames. Here, ##\tau## is the proper time along a straight line in space-time with ##\Delta t## being the difference between the endpoint time-coordinates and ##\Delta x## being the difference between the endpoint space-coordinates. This also changes what kind of coordinate transformations we can do in order for the proper time to be the same regardless of the coordinates. Instead of rotating both coordinate axes in the same direction as happens for rotations, the coordinate axes are rotated by the same angle in opposite directions.
In relativity, the proper time defined above is the only time that will be measured by any observer. A curve in space-time is called a world line and will generally describe the position of the observer as a function of time. The proper time of a world line, i.e., the “length” of the world line with the modified Pythagorean theorem, is the time a clock following that world line will measure, the time coordinate ##t## has no particular meaning other than that it happens to numerically be the same as the time measured by an observer for which the spatial coordinates are not changing. This is completely analogous with our previous example, where the value of the ##x##-coordinate was equal to the length of a line for which the ##y##-coordinate was not changing.
We can now do the exact same exercise as we did use regular geometry. Consider the following two world lines described in the coordinate system ##S##:
The first world line ##\gamma_1## has a constant ##x##-component while the second world line describes an observer travelling with velocity ##v##. The world lines may be parametrised as
$$x_1(t) = 0, \quad x_2(t) = vt.$$
We can now compute the proper time from the time coordinate taking values ##t=0## to ##t=t_0## for both world lines using the modified Pythagorean theorem and find that
$$\tau_1 = t_0, \quad \tau_2 = t_0\sqrt{1-\frac{v^2}{c^2}}$$
or, equivalently,
$$\frac{\tau_1}{\tau_2} = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \equiv \gamma,$$
where ##\gamma## is the famous gamma-factor of special relativity. In other words, the proper time elapsed for an observer at rest between two time coordinates will differ from the proper time elapsed for a moving observer between the same time coordinates by a factor ##\gamma##. This is the essence of time-dilation but, just as for the example we started with, it crucially depends on the coordinate system.
Taking a different coordinate system ##S’## where ##\gamma_2## describes a world line with constant ##x’##
the exact same argumentation will now lead us to conclude
$$\frac{\tau_1′}{\tau_2′} = \sqrt{1-\frac{v^2}{c^2}} = \frac{1}{\gamma}.$$
This is the exact opposite relation as that we found in the coordinate system ##S##, just as was the case in our first example! The resolution of this apparent mismatch is also completely analogous. We should not be surprised to find a different relation between the times elapsed between different ##t## coordinates and that elapsed between different ##t’## coordinates simply because the point on the curve ##\gamma_1## with the same ##t## coordinate as the point ##A## on ##\gamma_2## will not be the same as the point on ##\gamma_1## with the same ##t’## coordinate as ##A##:
This effect is called the “relativity of simultaneity” and simply states that two events which are simultaneous in one set of coordinates are generally not simultaneous in a different set of coordinates (simultaneous simply refers to having the same time-coordinate). As such, there is really nothing strange about the proper times to ##B## and ##C## along with ##\gamma_1## being different since they are simply not the same point.
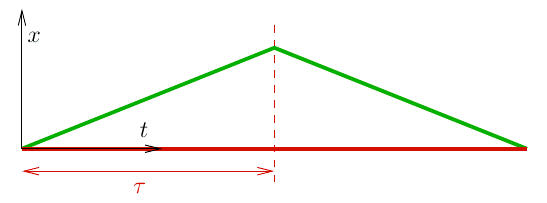
The twin paradox
The twin paradox is the analogue of our second example with two curves starting and ending at the same points. In the case of two twins, where one leaves to travel to a faraway land and later returns, the world lines in the coordinate system ##S## would look like:
Just applying the modified Pythagorean theorem it becomes clear that the proper times along the world lines are given by
$$\tau_1 = 2\tau, \quad \tau_2 = 2\tau \sqrt{1-\frac{v^2}{c^2}} \quad \Longrightarrow \quad \frac{\tau_1}{\tau_2} = \gamma$$
and therefore more proper time will pass for the twin staying behind, i.e., the red curve. Going to the coordinate system ##S’##, we can compute the relation between the proper time ##\tau’## taken for the travelling twin to reach the turnaround point and the proper time elapsed for the staying twin during the same ##t’## interval as
$$\frac{\tau_1′}2 = \tau’ \sqrt{1-\frac{v^2}{c^2}}, \quad \frac{\tau_2′}2 = \tau’.$$
However, just as in our example above, the relativity of simultaneity tells us that ##\tau_1’## is not equal to half the proper time elapsed for the staying twin until the reunion:
Instead, the change of geometry indicates that we are not counting part of the world line if we make this assumption and therefore underestimate the elapsed proper time. If taken properly into account, we would find that the time elapsed for the staying twin is longer also as computed by the travelling observer. This resolves the twin paradox and shows that it only appears due to not taking the relativity of simultaneity properly into account.
Professor in theoretical astroparticle physics. He did his thesis on phenomenological neutrino physics and is currently also working with different aspects of dark matter as well as physics beyond the Standard Model. Author of “Mathematical Methods for Physics and Engineering” (see Insight “The Birth of a Textbook”). A member at Physics Forums since 2014.
What do you think of this derivation of the space-time diagram from the travelling twin's perspective?
View attachment 187057
As described in this paper: http://arxiv.org/abs/gr-qc/0104077v2Thanks for the share!
Awesome.
That's something what students should crave for – that's how it should be! Thanks!
Cheers!
Thread closed briefly for Moderation…
Which I have shown to be incorrect regardless of how “experience” is interpreted.Your have claimed it but I do not think you have shown it.
How does experience relate to frames of reference? What is the reality associated with a frame of reference? It is all very to say the any chosen frame is valid but so is the question and to write the question off because of the way it is handled by geometry and analogues with space alone (which seems to me what you are effectively doing) might be presumptuous. Take the resolution of the twin paradox for example. It has a resolution and they agree, as I see it, because the number of ticks of the identical precise clocks that they carry in their pockets are different by a specific amount. Each clock is stationary for the respective twin (and measures proper time for that twin, as I understand proper time). This is agreeing that one has had more experience, so to speak, than the other, if time is a measure of experience.
The use of different frames may yield a different number of ticks for any person but the experience of time is the same for that person and the rate of ticks of perfect clocks in a persons pocket is does not vary for that person; as I see it.
Anyway, as A.T. suggests that it may be a matter of semantics, or definitions and/or it takes 2, or more, to argue.
That is more useful for understanding, than arguing about words.Thank you.
as is typical, the examples/problems relate to comparing parameters of observers in different frames of reference with each observer stationary with respect to their frame; consistent with what I have been writing.Typical, yes. Required, no. The first postulate is clear on that. There is nothing special about any frame, you can use the one where you are at rest, but it is not privileged. The use of an observer’s rest frame is a matter of convenience only. Because it is convenient it is commonly done. The first postulate allows this convenience but makes it clear that it is not mandatory.
My reasoning is that I am the observer in that frame of reference and that is my experience.Which I have shown to be incorrect regardless of how “experience” is interpreted.
What forces did you experience as a first-hand observer docking the boat?Are you asking about raw experience or calculated experience? If you are asking about raw experience then that would be the frame invariant four force e.g. as directly measured by an accelerometer. From that frame invariant raw four force you could calculate the frame variant three force in any frame.
I can do simple problems as presented in, say, the book to which I was referredThat is more useful for understanding, than arguing about words.
Your understanding of relativity is lacking and you seem to be interpreting things that people tell you not as they are written, but as they fit within your own ideas. I do not think this is a good way of learning.My understanding of relativity may be lacking but that is an unfair claim and declaratory statements that I am wrong are not explanations. Never mind, I can do simple problems as presented in, say, the book to which I was referred, I get that resolutions in (or should I say by use of) all frames are valid for the specific frame used, I get that spacetime intervals are invariant of the frame used and I get the resolution of the twin paradox using a Minkowski diagram. However, I have lost interest in being enlightened.
I am the equivalent of the observer for that frameAgain, and this cannot be repeated enough, there is no such thing as "an observer for a frame". Your understanding of relativity is lacking and you seem to be interpreting things that people tell you not as they are written, but as they fit within your own ideas. I do not think this is a good way of learning.
The forces someone directly "experiences" are frame invariant. Analyses in all frames must agree on those.“The Principle of Relativity does not deny that the force acting on an object is different as reckoned in two frames in relative motion.” Page 59 of my copy of the book. If that is incorrect then I picked a bad parameter.
OK my experience is not a frame of reference and I and not in a frame of reference but I am referring to frames in which I am represented as stationary. I am the equivalent of the observer for that frame and the measurements I take are the values for that frame. That is my experience, it relates directly to values of things represented in that frame.
What forces did you experience as a first-hand observer docking the boat?The forces someone directly "experiences" are frame invariant. Analyses in all frames must agree on those.
But note that the term "observer" is often used as a synonym for reference frame, and then "to observe" can also mean "measure frame dependent parameters", rather "direct frame invariant observation".
My reasoning is that I am the observer in that frame of reference and that is my experience.A frame of reference is a choice of how to interpret your experience. You are not "in" any frame of reference. Your experience is not a frame of reference.
See if you can get hold of a copy of Taylor and Wheeler's book "Spacetime Physics".Got it, assuming “Spacetime Physics Introduction to Special Relativity” is what you meant. I note, as is typical, the examples/problems relate to comparing parameters of observers in different frames of reference with each observer stationary with respect to their frame; consistent with what I have been writing.
Words fail me in trying to describe the complete insignificance of the frame in which I am rest when dealing with that problem.So you choose to analyse the problem when your frame is comfortably inertial. Forces can be different in different frames. Forces are valid for that frame in which they are analysed. Sure you can analyse the problem in any frame you like and get a valid result for that frame (for the observer in that frame). What forces did you experience as a first-hand observer docking the boat? You seem to contend that is not a meaningful question but it seems to me that if I do the measuring of parameters then the values I measure in the frame in which I am stationary are the appropriate valves for that frame. My reasoning is that I am the observer in that frame of reference and that is my experience.
OK, so how do I know what values to apply in any particular frame?See if you can get hold of a copy of Taylor and Wheeler's book "Spacetime Physics". The early chapter explaining exactly what a reference frame is (and equally important, is not) covers this question well.
OK, so how do I know what values to apply in any particular frame?That’s a pretty vague question. The corresponding vague answer is you apply the values that are correct for that particular frame.
If you can make a less vague question then I can probably make a less vague answer. But I have lost the point of this discussion altogether.
If you don’t like the analogy then you are free to not use it. Your opinion against it is valid, your arguments against it are not.
OK but it it is all relative and does not change that insistence that the frame in which I am stationary does not have special significance to me does not seem reasonable to me.Have you ever tried docking a powerboat in a stiff wind? Words fail me in trying to describe the complete insignificance of the frame in which I am rest when dealing with that problem.
So either the claim that “my rest frame is my experience” is wrong because it is not your (raw) experience or it is vacuous since any frame is your (calculated) experience.
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-4OK, so how do I know what values to apply in any particular frame?
By, experience I do not mean a raw impression but to include calculations based on my understanding of physics. … By experience I mean measurements of space and time, including calculations taking due account of time delays inherent in simple raw observation.That doesn’t salvage your argument at all. Your claim was that “my rest frame is my experience”. I showed that it is not with the usual meaning of experience. With this meaning there is still no frame that uniquely represents my experience since I can do “calculations based on my understanding of physics” in any frame.
So either the claim that “my rest frame is my experience” is wrong because it is not your (raw) experience or it is vacuous since any frame is your (calculated) experience.
insistence that the frame in which I am stationary does not have special significance to me does not seem reasonable to me.Nevertheless, that is essentially a direct result of the first postulate.
Similarly, even simultaneity is not something you experience.Some have interpreted experience kind of as you have and some interpreted it as I intended. By, experience I do not mean a raw impression but to include calculations based on my understanding of physics. Even I have not yet received a raw, when I do receive it and process it I may come to the conclusion that it happened simultaneously with an event I knew of previously and reason is that it happen at a far distant place.
My understanding is that I can apply frames of reference in which something is moving, which could be me, and a frame of reference in which that thing is stationary. I can personalise the frame of reference in which I am stationary because it relates to my experience and I call that my frame of reference. By experience I mean measurements of space and time, including calculations taking due account of time delays inherent in simple raw observation. Those measurements are the values of the variables of space and time in my frame. Other people would have different personalised frames of reference in which they are stationary. Transformations, between different personalised frames account for different experiences, part of which is the consideration of simultaneity; that is, whether events are simultaneous depends on the frame. Inanimate objects do not personalise, but we can relate to their parameters in our individual personalised frame in which we are stationary.
Have I misconceived relativity?
But if someone had carefully synchronized the clocks in any of those other frames, you'd have the same requirement imposed on your frame.In order to appreciate someone else's experience (measurements) I have to have to perform a transformation. In order for someone else to appreciate my experience they have to perform a transformation. That's relativity.
The reference frame doesn't yield measured simultaneity. Simultaneity is used to construct the reference frame.OK but it it is all relative and does not change that insistence that the frame in which I am stationary does not have special significance to me does not seem reasonable to me.
Not sure what you mean here. You define simultaneity based on the measurements and some convention, so it "agrees" with the measurements per definition.I was responding one of your posts which seemed to suggest I was using loose use of the experience as if it was a raw impression.
Rest frame was, perhaps, a bad choice of wording. What I meant was all frames in which I was stationary at the time, including non inertial frames of acceleration, which I guess correlates to the light cone. Yes/no?No, not even remotely. Each frame includes all events in spacetime, including all future events. Surely you do not believe that you experience the future.
Similarly, even simultaneity is not something you experience. A star 1000 light years away may go supernova as you blow out candles on your birthday cake, but the star going supernova is not part of your experience because it is outside of your past light cone. However, a star 1000 light years away that went supernova 1000 years ago could be part of your birthday experience because it is in your past light cone. You know it did not happen simultaneously with blowing out your candles, but your experience was that the star went bright as the candles went dark. That is the light cone and it has nothing to do with frames or simultaneity.
This explanation with the 2D analogue does not do it for me.That is fine. Not all analogies or explanations will do it for every person. You are certainly justified in your personal preference for any reason or for no reason at all. However, you need to be aware that the analogy is exceptionally solid. Your opinion-based objections are all legitimate, but so far your fact-based objections are all based on misunderstandings.
Personally, if you don’t like the analogy then I say you don’t need to use it. But the analogy is very common and powerful because of how accurate it is. It is far more exact than most other scientific analogies, so valid fact-based objections are relatively few and far between.
Fine, but having measured and accounted for signal delays simultaneity agrees with my measurement in a particular frame does it not?If your frame regards the actual emission events as equidistant from you, yes. The mere fact that you receive signals from events simultaneously tells you nothing about whether or not the events were simultaneous.
Fine, but having measured and accounted for signal delays simultaneity agrees with my measurement in a particular frame does it not?You would have had to account for signal delays to establish simultaneity, so naturally you will be able to use that very same procedure to verify that it was done correctly.
For other frames a transformation has to be performed.But if someone had carefully synchronized the clocks in any of those other frames, you'd have the same requirement imposed on your frame.
To insist the reference frame that yields measured simultaneity by me has nothing to do with my experience takes its own kind of convoluted thinking,The reference frame doesn't yield measured simultaneity. Simultaneity is used to construct the reference frame.
Fine, but having measured and accounted for signal delays simultaneity agrees with my measurement in a particular frame does it not?Not sure what you mean here. You define simultaneity based on the measurements and some convention, so it "agrees" with the measurements per definition.
It seems to me that this sort of debate undermines the very idea of an "insight" – and, in this case, an insight by an expert professional physicist. This is not clarififying a point made in the insight but a separate analysis, challenging – to some extent at least – the basis for SR and confusing the issue with a beginner's misconceptions about SR. The place for those is a separate thread.
In Relativity, even accounting for signal delays, still leaves you with different simultaneity for frames in relative motion.Fine, but having measured and accounted for signal delays simultaneity agrees with my measurement in a particular frame does it not? For other frames a transformation has to be performed.
To insist the reference frame that yields measured simultaneity by me has nothing to do with my experience takes its own kind of convoluted thinkingBasing simultaneity on what you "experience" doesn’t even work in classical mechanics, due to signal delays. In Relativity, even accounting for signal delays, still leaves you with different simultaneity for frames in relative motion.
Again, there is no "reference frame" for an observer's experience. It does not matter what frame you choose to label and interpret your events, your experience will be exactly the same.
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-3I think I see where you are coming from simply because the transformations when used will allow for all observers to agree about my experience of simultaneity when their experience is different from mine. To insist the reference frame that yields measured simultaneity by me has nothing to do with my experience takes its own kind of convoluted thinking, to my mind (and is an arbitrary abstract choice). But, OK you are the expert and I am not insisting that you are incorrect; just trying to learn.
However, that implies that an observer and the reference frame for their experience is not arbitrary.Again, there is no "reference frame" for an observer's experience. It does not matter what frame you choose to label and interpret your events, your experience will be exactly the same.
All frames will agree that you received light from the strikes simultaneously. All frames will agree that the flashes happened earlier than you saw them. Because they use different definitions of simultaneity they will not agree that the flashes happened simultaneously.
Your experience is not a frame. A frame is a tool for interpreting your experience.Which has always been my understanding. However, that implies that an observer and the reference frame for their experience is not arbitrary. And I am sorry that my fruit saladedy language is spurned but the frame innately used for my experience is not arbitrary and is a relationship that gives a sense of 'occupying' that frame.
? I ask because if I measure two bolts of lightning in different locations to be simultaneous it seems that my experience of measuring simultaneity can be arbitrarily disregardedAll frames will agree that you received light from the strikes simultaneously. All frames will agree that the flashes happened earlier than you saw them. Because they use different definitions of simultaneity they will not agree that the flashes happened simultaneously.
Your experience is not a frame. A frame is a tool for interpreting your experience.
I am sorry, but this reads as word sallad.
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-3I am sorry you feel that way.
you are stating things as if your own understanding must be the correct one rather than as if trying to understand what is going on
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-3That is not my intent.
The underlying thing to understand (without which you can never properly understand time dilation or any other effect in SR) is that simultaneity is relative
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-3That simultaneity is relative is something that I think I appreciate.
Your rap over my knuckles is acknowledged. However, it seems that an observer may chose a frame of reference to deem whether events are simultaneous and I dare to ask whether that is correct? I ask because if I measure two bolts of lightning in different locations to be simultaneous it seems that my experience of measuring simultaneity can be arbitrarily disregarded (and in a sense of using transformations to use a different frame of reference it can but to disregard my experience seems to involve its own convoluted rationale).
Only for the spacetime interval.No. The choice of frame is completely arbitrary. That choice is also a definition of what "space" and "time" (in the sense of coordinate timel mean for this reference frame, so concepts such as length and duration follow from this. Length contraction and time dilation are the result of defining different things as the length of an object or its duration.
The Euclidean analogy to this is a rectangular table. Whether it's a long, narrow table or a short, wide one depends on an arbitrary choice of which direction we call "across" and which "along". That choice is arbitrary, and need not correspond to where you happen to be standing.
However, so long as the twins separate in different inertial frames each is older than the other, forever in each's own frame. That, I imagine, is time dilation.More or less (although see my comment below on your "more precise" comment on the twin paradox). The important thing is that those answers depend on an arbitrary choice of what you want to call "at the same time as" one twin is aged 30. You can fairly easily construct a frame in which they are both always the same age. The difference with the twin paradox is that the twins reunite and, at that point, there must be a non-arbitrary answer to how old they both are.
Except that my rest frame is my experience.Definitely not. Say a supernova appears in the sky tonight. Your experience is that a supernova appeared on December 13th 2018. That's all. If you pick a reference frame, you can then decide how far away the supernova was and when it happened. If you pick a different frame then you will come up with a different answer. But no choice of frame changes your personal experience of seeing a supernova and checking the calendar.
Frames have nothing to do with experience. They are all about interpretation of that experience, and multiple interpretations are possible.
What I meant was all frames in which I was stationary at the time, including non inertial frames of acceleration, which I guess correlates to the light cone. Yes/no?No.
To be more precise about the twin paradox. So long as each twin occupies a different inertial frame continuing to separate apart from the other's frame then each continues to age faster than the other.No. Nobody "occupies" a frame. As long as each twin remains moving inertially and chooses to use their inertial rest frame to interpret information about their twin, they will regard themselves as older. They can, at any time, adopt a different frame or just a different simultaneity convention and come up with a different answer.
As I see it, time is not independent of the location in space, but a restriction on the 3D location that can be occupied. In the 2D analogue there is no such interdependence/restriction.I am sorry, but this reads as word sallad.
Furthermore, position in space is frame dependent and therefore arbitrary.
What I meant was all frames in which I was stationary at the time, including non inertial frames of acceleration, which I guess correlates to the light cone. Yes/no?No. What you experience has nothing to do with arbitrary coordinate systems. Convoluting and changing your statements is not going to change that.
So long as each twin occupies a different inertial frame continuing to separate apart from the other's frame then each continues to age faster than the other.This again shows fundamental misunderstanding of SR. Inertial frames are not things to be ”occupied”. Anything that exists in one frame exists in all frames.
That, I think, exemplifies what requires insight; or just plane acceptance because it seems to be implicitly verified by experiment.And the insight is that this is no stranger than the Euclidean analogue I mentioned. The only difference is that spacetime has a different geometry through the modified Pythagorean theorem. Why it has that geometry is a different question, but results from the SR postulates. The number of dimensions has nothing to do with this.
However, I suggest that the insight would be to understand how the experience of time and space for each occupier of different frames differs, which is counter intuitive.Which you would understand if you read the insight. The insight is that, geometrically, it is completely analogous to the Euclidean case presented. Saying that it is not and instead banging your head on your own misunderstandings is not going to change this fact. You started by admitting that you are a novice in relativity, but you are stating things as if your own understanding must be the correct one rather than as if trying to understand what is going on. I do not think this will serve you well in the long run. Note that many of the people you are conversing with here are anything but novices when it comes to relativity.
I am not claiming that the Insight must be useful to everyone, but the fact of the matter is that the ideas behind time dilation are exactly analogous to the Euclidean case presented. It is also not intended to teach you why spacetime geometry is different, just about why this difference leads to some sign changes but otherwise time dilation is exactly the same effect as that discussed in the Euclidean setting.
Also note that inertial frames do not ”experience” time, they have a time coordinate, which is a different concept. The underlying thing to understand (without which you can never properly understand time dilation or any other effect in SR) is that simultaneity is relative, ie, events that are simultaneous in one frame are generally not in another.
If you take the ratio of the projections onto the time axes that will give you the amount of time dilation. That ratio is not random, it depends on the angle that the time axes make with each other, which in turn depends on the relative speed.
Reference https://www.physicsforums.com/threa…n-and-the-twin-paradox-comments.842793/page-3Indeed, it is a mathematical construct that works. However, I suggest that the insight would be to understand how the experience of time and space for each occupier of different frames differs, which is counter intuitive. This explanation with the 2D analogue does not do it for me.
I was talking about the lengths of the projections of the line (object) onto the axes in the analogue, which was just about 2 D space.If you take the ratio of the projections onto the time axes that will give you the amount of time dilation. That ratio is not random, it depends on the angle that the time axes make with each other, which in turn depends on the relative speed.