How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics

In Chapter 37 of “The Feynman Lectures on Physics Volume 1,” Richard Feynman famously wrote that the mystery of wave-particle duality in the double-slit experiment is:

a phenomenon which is impossible, absolutely impossible to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by “explaining” how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics.

In this Insight, I want to show you how Brukner and Zeilinger’s information-theoretic principle of Information Invariance & Continuity as justified by the relativity principle solves this mystery. In How Quantum Information Theorists Revealed the Relativity Principle at the Foundation of Quantum Mechanics, I explained how Information Invariance & Continuity entails that everyone measures the same value for Planck’s constant h, regardless of the relative spatial orientation of their inertial reference frames. Obviously, that can be justified by the relativity principle, i.e., the laws of physics (including their constants of Nature) are the same in all inertial reference frames, which I call “no preferred reference frame (NPRF).” While it is commonly assumed that different inertial reference frames are only related by different relative velocities, they are in fact also related by different relative spatial orientations, spatial locations, and temporal locations. The entire set of transformations between such reference frames that guarantees everyone will measure the same value for the speed of light c (the light postulate of special relativity), is the set of Poincare transformations, i.e., Lorentz boosts, spatial rotations, spatial translations, and time translations. The light postulate is justified by the relativity principle and special relativity (SR) follows from that fact, so I will characterize SR as following from NPRF + c. Likewise, the axiomatic reconstructions of QM based on information-theoretic principles show how one can derive the (finite-dimensional) Hilbert space of QM from Information Invariance & Continuity, which can be justified by NPRF, so I will characterize QM as following from NPRF + h.

The axiomatic reconstructions of QM based on information-theoretic principles render QM a principle theory, as I explained in A Principle Explanation of the “Mysteries” of Modern Physics. In general, a principle explanation solving some mystery can be written:

Compelling fundamental principle $\rightarrow$ Justifies empirically discovered fact $\rightarrow$ Dictating the mystery

In this case, we have:

Relativity principle $\rightarrow$ Justifies Information Invariance & Continuity $\rightarrow$ Dictating wave-particle duality for the double-slit experiment

Recall from “How Quantum Information Theorists Revealed …” for the spin-$\frac{1}{2}$ particle, Information Invariance & Continuity entails that everyone measures the same value for h regardless of the orientation of their Stern-Gerlach (SG) magnets, i.e., regardless of the spatial orientation of their inertial reference frames. Since we’re talking about a constant of Nature having the same value in all inertial reference frames (related in this case by spatial rotations), this empirically discovered fact can be justified by NPRF. To see how the classical formalism follows on average from the quantum formalism, I showed how the classical constructive account predicts that atomic dipoles along $\hat{z}$ should be deflected by $\cos{\left(\theta \right)}$ when they pass through SG magnets oriented at $\hat{b}$ making an angle $\theta$ with $\hat{z}$. Instead, we find only full deflections of $\pm 1$ $\left(\pm \frac{\hbar}{2}\right)$ along $\hat{b}$ that average to $\cos{\left(\theta \right)}$. This gives you ‘average-only’ projection of spin angular momentum between these reference frames as a consequence of NPRF + h.

For polarization, Information Invariance & Continuity entails that everyone measures the same value for h regardless of the orientation of their polarizing filter, i.e., regardless of the spatial orientation of their inertial reference frames, which is easily justified by NPRF just like the spin-$\frac{1}{2}$ particle. The empirically discovered fact in this case is that a photon either passes or it doesn’t pass through a polarizing filter, i.e., there are no ‘partial photons’ passed by a polarizer. We can say that our empirically discovered fact in this case results because $E = hf$ and if a fractional photon passed through a polarizer, the value of h would be reduced by that fraction, so you would have two inertial reference frames related by a spatial rotation whereby h had two different values in violation of NPRF. This gives you ‘average-only’ transmission of polarized electromagnetic energy between these reference frames as a consequence of NPRF + h. In this case, the classical wave mechanics follows on average from the distribution of photon (particle) energy per quantum mechanics. Now let’s provide a similar NPRF + h solution to the mystery of wave-particle duality in the double-slit experiment.

Our measurement context will be an interference pattern where we can obtain a wavelength $\lambda$ whence momentum $p = \frac{h}{\lambda}$. That means our qubit is that of Figure 1 with outcomes $|\text{BS Yes}\rangle$ of total constructive interference at a maximum (Both Slits Yes) and $|\text{BS No}\rangle$ of total destructive interference at a minimum (Both Slits No). [Since these are momentum states they are complementary to the “which slit” states $|\text{S1 Yes}\rangle$ (Slit 1 Yes) and $|\text{S2 Yes}\rangle$ (Slit 2 Yes) for position when measurements of position, momentum or superpositions thereof are being measured (Figure 2).] Our state is $|\psi\rangle = |\text{BS Yes}\rangle$ and the measurement in this context will be a spatially localized detector moved a distance x along the interference pattern from the central maximum toward a minimum on either side (as shown in Figures 3 and 4). The amount of momentum it records at each location along the interference pattern depends on how much constructive interference exists at that location, so it will start from a maximum and gradually diminish to zero at the adjacent minimum where there is no constructive interference for the state $|\psi\rangle$.

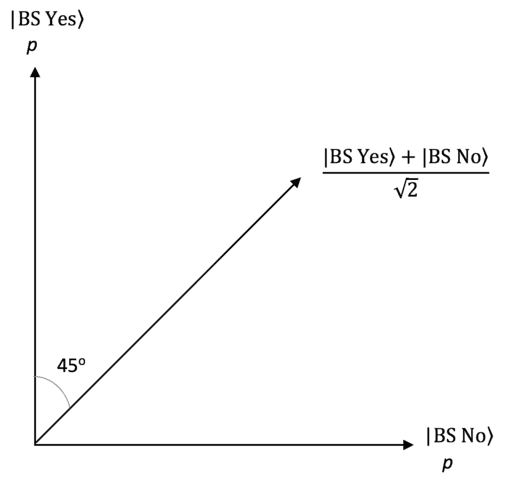
Figure 1. Hilbert Space Qubit for Momentum Measurements in the Double-slit Experiment.

 

 

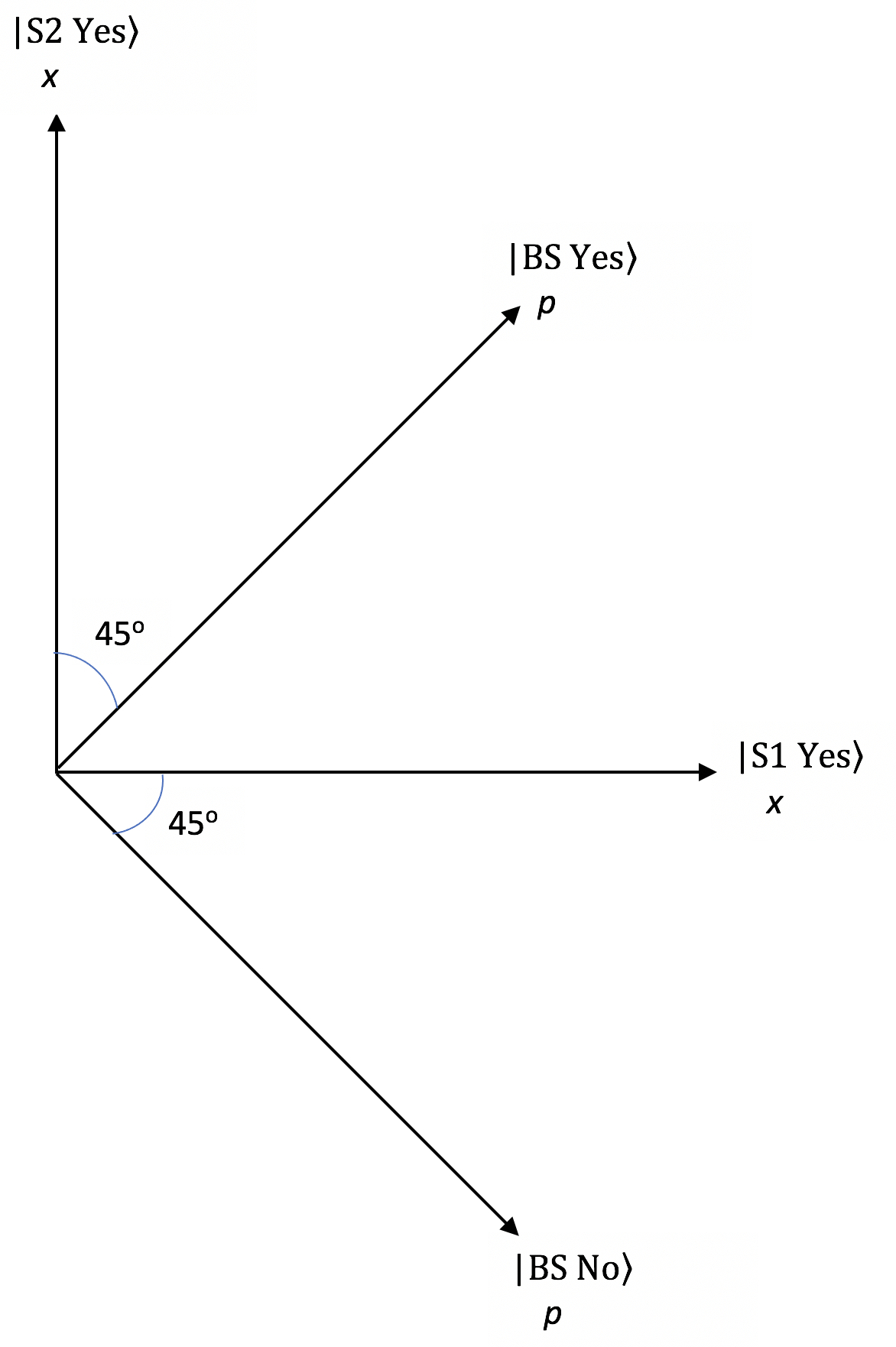
Figure 2. Hilbert Space Qubit for Measurements of Position, Momentum and Superpositions Thereof in the Double-slit Experiment.

 

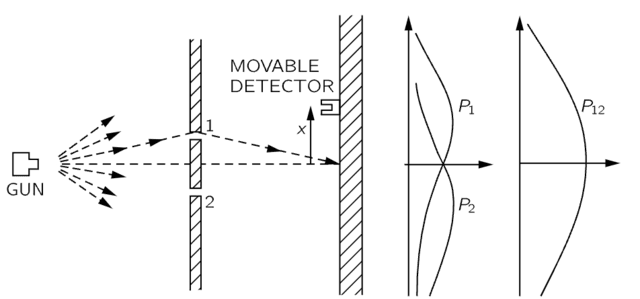
Figure 3. Outcome of the Double-slit Experiment with Bullets per Feynman.

 

 

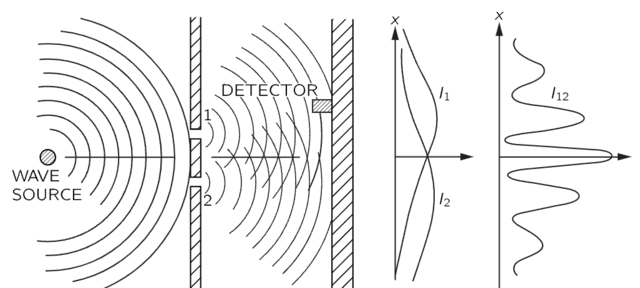
Figure 4. Outcome of the Double-slit Experiment with Water Waves per Feynman.

 

For example, with $|\psi\rangle = |\text{BS Yes}\rangle$ the electric fields $E_1 = E_2$ of the electromagnetic waves from the two slits add in phase at the central maximum to $E_o$ (say) and we have total constructive interference while they are totally out of phase and add to zero at the adjacent minimum. At any point between the central maximum and adjacent minimum the electric field amplitude is given by $E_o\cos{\phi}$ where $\phi = \frac{\pi d \sin{\theta}}{\lambda}$ with the angle $\theta$ and slit separation d as shown in Figure 5. So, when $\phi = \frac{\pi}{4}$ the electric field is $\frac{E_o}{\sqrt{2}}$ and the electromagnetic wave intensity (proportional to the wave momentum per the Poynting vector) is half that at the maximum. This will correspond to the Hilbert space vector $\frac{|\text{BS Yes}\rangle + |\text{BS No}\rangle}{\sqrt{2}}$ in the quantum case (Figure 1).

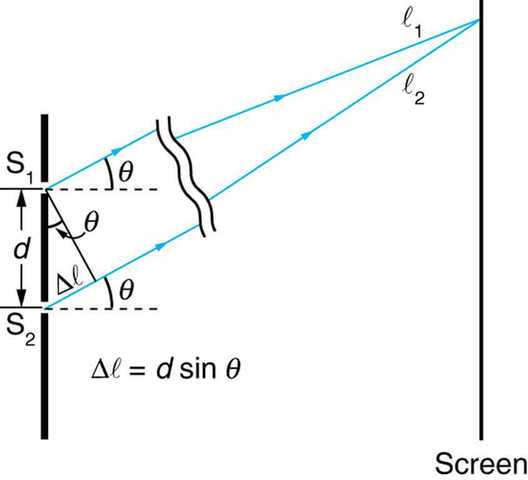
Figure 5. Double-slit Interference per Classical Wave Mechanics.

Mechanically speaking, this is exactly how Zeilinger’s experiment worked in Figure 6 where his detector recorded counts over a 60-second time interval at each location along the interference pattern (see also Feynman’s versions of the double-slit experiment with bullets, water waves and electrons in Chapter 37 of “The Feynman Lectures on Physics Volume 1,”). A classical wave measurement of this sort would obtain momentum in a continuum sense (like water waves in Figure 4), rather than discrete detector clicks (like bullets in Figure 3), at each spatial location. Of course, each detector click represents a quantum of momentum/energy, so counting detector clicks is still a measurement of momentum (over the area of the detector where each click delineates a unit of time).

Figure 6. Double-slit Experiment Outcomes per Zeilinger [1].

As with the polarization experiment, we then reduce the rate at which momentum is emitted by the source so that only one quantum of momentum $p = \frac{h}{\lambda}$ is ‘passing through’ the slits at a time. The classically continuous wave description says p will be distributed spatially along the detector, so our spatially localized momentum measurement described above will measure a fraction of the momentum $p = \frac{h}{\lambda}$ at any given location x, which means h is reduced precisely by that same fraction in the inertial reference frame at x. Since fractional measurements of h are forbidden by NPRF (our inertial reference frames here are related by spatial translations in x), our momentum measurements at each point x instead obtain a number of quanta (each with the same value for h in $p = \frac{h}{\lambda}$) per fixed time (60 seconds in Zeilinger’s experiment). These counts are then normalized relative to that at the central maximum for our quantum distribution, so that the continuum distribution of momentum along the interference pattern predicted by the classical wave interference analysis obtains on average.

This explanation of the double-slit experiment per NPRF + h and the qubit shows that Feynman was essentially correct. The mystery of the double-slit experiment resides in the fact that NPRF + h demands we obtain quanta of momentum $p = \frac{h}{\lambda}$ in the inertial reference frames associated with the locations x (as with bullets in Figure 3), rather than a continuum of wave intensity (as with water waves in Figure 4). However, the quantum measurement context is that for momentum p, so an interference pattern allowing us to compute $\lambda$ for use in $p = \frac{h}{\lambda}$ is required. Therefore, the interference pattern per classical wave mechanics is what must obtain on average in this quantum mechanics context as in the momentum measurement of Zeilinger’s Figure 6. That is, the mystery of wave-particle duality in the double-slit experiment follows from the fact that the quantum case doesn’t conform to the classical case of particles or the classical case of waves, but must be a combination of both due to NPRF + h. In all three examples, NPRF + h demands that a classically continuous quantity (angular momentum, polarization, momentum) be quantized, so that you have to take an average to recover the classical continuity. That is how quantum information theory’s principle of Information Invariance & Continuity, as justified by the relativity principle, solves what Feynman called “the only mystery” of QM in principle fashion.

 

1. Anton Zeilinger, “Why the quantum? ‘It’ from ‘bit’? A participatory universe? Three far-reaching challenges from John Archibald Wheeler and their relation to experiment,” in Science and Ultimate Reality: Quantum Theory, Cosmology and Complexity, John D. Barrow, Paul C.W. Davies and Charles L. Harper, Jr. (eds.), (Cambridge Univ Press, Cambridge, 2004), pp 201-220.