How to Better Define Information in Physics

When I ask questions about the conservation of information I frequently get the reply, “It depends on what you mean by information.”   So, I researched how to better define information.  What I found is almost more interesting than the conservation question.  That sounds like the makings of a fun PF Insight article, so here goes.

This article is a survey of information and information-conservation topics in physics. It is intended for an amateur physics audience.  To make this article suitable for all levels of readers, most of my references are to Professor Leonard Susskind’s video courses, or to Wikipedia.

Start Simple

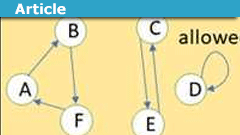
In both his Classical Mechanics[i] and Statistical Mechanics[ii] courses, Susskind begins with simple examples of the allowable laws of physics.  Consider a system with 6 possible states, A-F.  We are interested in the allowable rules of how the system can evolve.  In the blue example below, A goes to B. B to C, C to D, D to E, E to F, F to A, or ABCDEF overall.  The yellow example is more complex with cycles ABF CE and D, but they are still allowable.  Allowable rules are deterministic, time reversible[iii], and they conserve information.    For each of those allowable laws, we could write corresponding equations of motion.  What is the information conserved?  At any stage, we can calculate how we got there (the past) and where we’ll go next (the future), and which cycle (such as yellow ABF) we belong to.

 

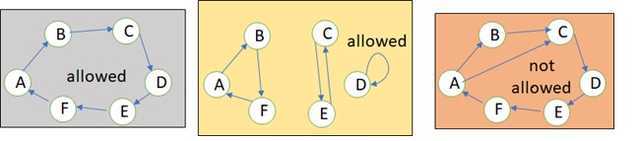
The red example, has two arrows coming out of A, and C has two arrows coming in.  Those are not deterministic, not time-reversible, and do not conserve information, and thus are not allowed.

Next, consider a 6-sided die.   The die has 6 microstates.  Let’s define I to be the information in this system or the number of microstates.  What do we know about the die’s position?  Maximum knowledge K occurs when we know exactly which side is up.  Minimum knowledge occurs when we have no idea about the position.  We can define entropy E, as being proportional to our uncertainty about the position.  Because of the way we defined I and E, then we can say trivially that K=I-E or I=K+E.  I should add that K could also be called “knowability” or “observability” just to emphasize that there is no need for an intelligent being in physics.

First off, we have to be clear about the rather strange way in which, in this theory, the word “information” is used; for it has a special sense which, among other things, must not be confused at all with meaning.  It is surprising, but true, from the present viewpoint, two messages, one heavily loaded with meaning, and the other pure nonsense, can be equivalent as regards information.  — Warren Weaver, The Mathematics of Communication, 1949 Scientific American.

Those definitions of entropy and that relationship cannot be applied literally in other physics contexts, but they are nevertheless useful as we will see in other contexts.  However, there is a familiar everyday life analogy.   A 1TB hard drive can store 1TB of information, but when it is new or freshly erased, it contains near-zero knowledge.

Consider 4 gas molecules in a box. [I chose the small number 4, to avoid thermodynamics definitions.] The number of possible microstates is proportional to the number of molecules.  If the 4 molecules were bunched in one corner then we have better knowledge of their positions than if they are distributed throughout the box. The point is that entropy (and thus knowledge) can vary with the state of the system, whereas the number of microstates (information) does not vary with state.

That leads me to definitions that we can use in the remainder of this article.  “Knowledge and Entropy are properties of the system and the state of the system (and possibly external factors too).  Information is a property of the system and independent of the state.[iv]” In my opinion, lack of attention to that distinction between information and knowledge is the origin of many misunderstandings regarding information in physics.

Microstates, Macrostates, and Thermodynamics

A definition of information consistent with our simple cases is “the number of microstates.” Susskind says[v] that the conservation of information could also be described as the conservation of distinction.  Distinct states never evolve into more or fewer distinct states.

In thermodynamics, a process can be reversible or irreversible.  In thermodynamics, we also have the famous 2^nd Law.  However, thermodynamics uses macroscopic quantities including temperature.  But, in this article, we are discussing microstates, not macrostates, so some thermodynamic concepts and definitions do not apply.

Notwithstanding the above, I can’t resist mentioning  that in Boltzmann’s definition[vi], entropy is “a measure of the number of possible microscopic states (or microstates) of a system in thermodynamic equilibrium, consistent with its macroscopic thermodynamic properties (or macrostate).”   It then follows that the total number of microstates (information) is greater than or equal to the entropy.  For the case with exactly one macrostate, then entropy and information are equal.   That is consistent with information as being independent of the (macro)state.

An amusing aside.  Susskind calls[vii] Conservation of Information the -1^st law of thermodynamics, and the 0^th law of thermodynamics is, “If A is in thermal equilibrium with B, and B with C, then A must be in thermal equilibrium with C”, and the more familiar 1^st law that we teach students is Conservation of Energy.   He emphasizes that information is more fundamental than entropy and energy.

Information in Classical Mechanics

In classical mechanics we learn of phase space;  meaning the multidimensional space formed by position x and momentum p degrees of freedom.  In A below, we see a depiction of phase space (showing on only one x and one p axis).  Each distinct point can be considered a possible microstate as in A.  In time, the states can evolve to other places in phase space, as in B.  But the trajectories never fork, and never converge (as in C), thus conserving the number of distinct microstates.  A, B, and C are the continuous analogs of the discrete evolutions (blue, yellow, and red boxes) we started with above.

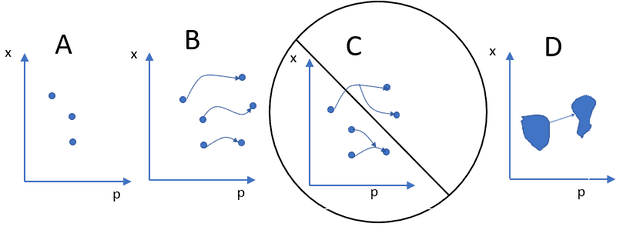
Even better, Liouville’s Theorem[viii] says that if we choose a region in phase space (see D above); it evolves in time to different positions and shapes, but it conserves the volume in phase hyperspace.    Liouville’s Theorem is often said to express the conservation of information in classical mechanics.   Referring to the little picture on the right, drawing the boundaries of the volume determines the system, and thus the information.   The shape of the boundary (state) evolves with time.  Evolution can be ordered or chaotic.

Is entropy conserved too?  In general, no. (again system↔information state↔entropy)  However, if we fork the definition of entropy to include coarse versus fine grained entropy, that leads to an interesting side topic.

In classical mechanics, we should also consult with “the most beautiful idea in physics”, Noether’s Theorem.  That is the theorem that says that every differentiable symmetry of the action of a physical system has a corresponding conservation law.

It would be nice to use Noether’s Theorem to prove a relationship between information conservation and some symmetry of nature.   I found one source that says that Noether’s Theorem proves that information conservation is a result of time reversal symmetry[ix].   Another source says that it is not[x].

Alas, time reversal is discrete and non-differentiable, so that won’t work.  How about some other symmetry?   If $I$ represents the quantity of information, and if we wish to prove that $\frac{dI}{dt}=0$ using the Principle of Least Action, then the quantity of information $I$ should appear in the expression for the action.  As far as I know, it does not.   So, it seems that we can’t use Noether’s Theorem to prove information conservation.

Information in Quantum Mechanics

Unitarity is one of the postulates of Quantum Mechanics[xi].  Unitarity is also said to be the foundation of the conservation of information.  (By the way, I exclude from this discussion all interpretations of quantum mechanics.)

Unitarity is also said to conserve probability.  Huh?  So now information is probabilities?    These Wikipedia sources[xii] say yes, conservation of probabilities implies conservation of information.

In another context[xiii], Susskind said that if quantum evolutions were not unitary, the universe would wink out of existence.   I believe that what he was referring to is this.  If evolutions were sub-unitary, then the probabilities would shrink at each time evolution, until only one microstate remained for the entire universe.  If they were super-unitary, the probabilities would increase with each evolution to the point where the identity of particles would be smeared to oblivion.  In either case, the universe as we know it could not exist.  I interpret all that as saying that the number of microstates (hence information) is conserved in quantum evolution. One might also say it as the system is conserved while the state of the system evolves.

Here’s another example. 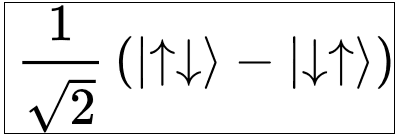 Consider a system of two free electrons.  Electrons are spin ½ particles, and we can know their spins because there is an observable for a spin.  Now consider what happens if the two electrons become fully entangled in the singlet pair state which is spin 0.  There is no observable for the singlet to return the spins of the component electrons.  This is a time of evolution where information is conserved, but knowledge (or knowability) is not conserved.  The state changed, but the system remained the same.   Remember also that the electrons can also become disentangled thus restoring the original knowledge, while the information of the two-electron system remains invariant throughout.

This example illustrates why I prefer to define information and knowledge as distinct things.

By the way, there is also a quantum version of Liouville’s Theorem[xiv] that says (guess what) quantum information is conserved.

Information in Cosmology & General Relativity

Conservation of information at the origin of the universe is the question that first interested me in this topic.  I never found an answer to that, and probably never will.

None of Special Relativity, General Relativity, or Cosmology directly address information.  However, there is a red-hot issue; the so-called Black Hole Information Paradox[xv].

Stephen [Hawking] claimed that “information is lost in black hole evaporation,” and, worse, he seemed to prove it. If that was true, Gerard [’t Hooft] and I realized, the foundations of our subject were destroyed. —Leonard Susskind[xvi]

By the way, the Wikipedia article about the paradox offers yet another definition for information conservation.

There are two main principles in play:

• Quantum determinism means that given a present wave function, its future changes are uniquely determined by the evolution operator.
• Reversibility refers to the fact that the evolution operator has an inverse, meaning that the past wave functions are similarly unique.

The combination of the two means that information must always be preserved.

This so-called black hole paradox was also the topic of at least 15 PF threads.  In my opinion, many of those discussions were spoiled because participants argued about information with differing definitions of the word information in their heads. Nevertheless, the debate continues at levels far above my head.   The Wikipedia article summarizes the latest arguments for and against.   It also points to another interesting related side topic, The Holographic Principle, which in turn leads to The Limit on information density which leads to The Bekenstein Bound which also talks about limits on information density.  Does all this make you feel that you are falling into the rabbit hole?  I feel that way.

By the way, I’m delighted that The Bekenstein Bound provides the only example I know of an equation relating information in bits to ordinary physical quantities.

$H ≤ \frac{2\pi cRM}{\hbar ln 2} ≅ 2.5769082 \times 10^{43} \frac{bits}{kg\cdot m}\cdot M \cdot R$

Where H is the Shannon entropy, M is mass in kg, and R is the radius in m of a system.

Utility

Laymen frequently hold the false impression that the purpose of science is the discovery of truth.   Scientists are more interested in what is useful, and less interested in the truth.  Truth can be very philosophical, but usefulness is proved by use.

Unfortunately in physics, information is more interesting than it is useful.  If  $I$ represents a quantity of information measured in bits (or qubits), how do we calculate it? How do we measure it?  I don’t know exactly how many bits it takes to completely describe a photon, or a nucleus, or a lump of coal.  The lack of ability to define and measure a numerical quantity for information prevents me from using information with  The Principle of Least Action,  or doing a before-after information balance on an event such as beta decay.

In a beta decay event,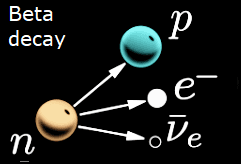 a neutron decays into a proton $p$, an electron $e^-$, and an electron antineutrino $\bar{\nu}_e$.  We know that momentum, energy, and information should all be conserved.  Therefore, we can write a momentum balance equation or an energy balance equation, but how about an information balance equation?   Suppose we have a function  $I()$ that returns the quantity of information of a particle. We should be able to write $I(n)=I(p)+I(e^-)+I(\bar{\nu}_e)$.   Since $I()$ should always be nonzero positive, it also seems conclusive that the information in a neutron must be greater than the information in a proton.  But we have no such function I(n).   We can’t say how much information is in a neutron, yet we can write equations relating I(n) to other information.  Hence, my complaint about the information’s lack of utility.

Information and Causality

Causality is a fundamental principle in physics.   There is no theory of causality, nor is it derived from other laws.   Causality never appears explicitly in equations.  Yet if causality was violated, physics and the universe would be thrown into chaos.

Conservation of Information (COI) is a fundamental principle in physics.   There is no theory of COI, nor is it derived from other laws.  COI never appears explicitly in equations.  Yet if COI was violated, physics and the universe would be thrown into chaos.

Yet the following subjective statements are also true. “Causality means that the cause comes before the effect,” is instantly understood and accepted by almost everyone. “COI means that information is never created or destroyed.,” is instantly misunderstood and challenged by almost everyone.

Conclusion

Let’s summarize.  In physics, the word information is closely related to microstates and probabilities.  In some limited circumstances information is equal to entropy, but in most cases not.   Information should never be confused with knowledge despite what natural language and the dictionary say.  And never confused with the knowledge of intelligent beings. Despite our inability to quantify information, conservation of information seems firmly established in many contexts.  Limits to information density also appear to be well-founded, again despite our inability to quantify it.   Information in physics has tantalizing parallels with Shannon Information Theory in communications and computer software, but it is not identical.

On PF, we frequently remind members that energy does not exist by itself in space; energy is a property of fields and particles.  Should we say the same thing about information, that it is a property of fields and particles?  Some people invert that view and speculate that information is the building block on which fields particles and even reality are built[xvii].  A third view is that there is no such thing as information as a physical quantity, it is just a lingual artifact of our way of speaking.   This article brings no clarity to those questions.  All we have is hand waving.  I blame that on less-than-useful definitions.

The above notwithstanding, the future sounds bright.  Professor Susskind has been touring the country with a series of lectures including ER=EPR in the title[xviii].  He is discussing the research direction of his Stanford Institute for Theoretical Physics.   He said that they are looking toward information theory to unite quantum mechanics with general relativity.   Of course, it remains to be seen if they will succeed.  If they do, Nobel Prizes will surely follow.   But for me, their success would hopefully produce one thing even more welcome; namely, a more useful quantitative definition of the word information.

A postscript.  Just as I was wrapping up this article, I stumbled across another Susskind quote[xix] that turned everything on its head.

When a physicist, particularly physicists of my particular interest, talks about quantum information, they are usually talking about entanglement.  Leonard Susskind.

Ay ay ay; I have a headache.

---

What is your definition of information in physics?  Please contribute it to the discussion thread.  But no QM interpretations, please.  Also, quantitative definitions please; not examples.  Finally,  please remember that a bit is a unit, not a definition.

---

Thanks to member @Dale for his helpful suggestions.

---

References:

[i] Susskind, Classical Mechanics, Lecture 1

[ii] Susskind, Statistical Mechanics, Lecture 1

[iii] In thermodynamics we have both reversible and irreversible processes.  Information depends on microstates.  Thermodynamics depends on macrostates, so it does not apply here.

[iv] Susskind, Statistical Mechanics, Lecture 1

[v] Susskind, Classical Mechanics, Lecture 5

[vi] Wikipedia: Boltzmann’s principle

[vii] Susskind, Statistical Mechanics, Lecture 1

[viii] Wikipedia: Liouville’s theorem (Hamiltonian)

[ix] PBS Space Time Why Quantum Information is Never Destroyed

[x] Wikipedia: Symmetry (physics)

[xi] Wikipedia: Mathematical formulation of quantum mechanics

[xii] Wikipedia: Probability Current, Continuity Equation

[xiii] Susskind Book: The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics

[xiv] Wikipdeia: Quantum Liouville equation, Quantum Liouville”, Moyal’s equation, Quantum Liouville equation

[xv] Wikipedia: Black Hole Information Paradox

[xvi] Susskind Book: The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics, page 21.

[xvii] Scientific American: Why information can’t be the basis of reality

[xviii] This Youtube search, returns 3,480 hits on ER=EPR.  ER refers to Einstein-Rosen bridge or wormhole, a solution of General Relativity. EPR refers to the Einstein–Podolsky–Rosen paradox regarding quantum entanglement. So ER=EPR is a clever way to suggest the unification of GR and QM.

[xix] Susskind: ER=EPR but Entanglement is Not Enough