How to Solve a Multi-Atwood Machine Assembly

Introduction

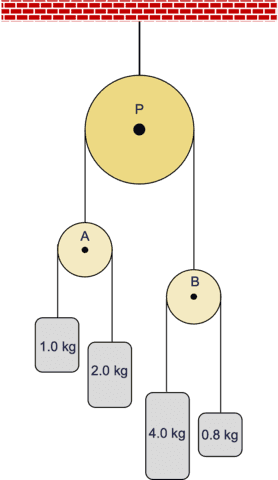
A double-double (AM-2) Atwood machine.

The figure on the right shows a “double-double” Atwood machine with three ideal pulleys and four masses.  All pulleys are released from rest simultaneously.  Which of the choices below describes the angular motion of the top pulley P after some time has elapsed and why?

1. It rotates clockwise with increasing angular speed.
2. It rotates counter-clockwise with increasing angular speed.
3. It remains at rest.

If your immediate thought, gentle reader, was “idk where to start” or “let me draw a free body diagram” or “let me write down the Lagrangian”, please read on.  You will see how you can reach the correct answer in one line on the back of an envelope. In addition, you will learn how to find the accelerations of all the masses and pulleys in a multi-Atwood machine assembly relying on nothing more than three simple rules and Newton’s second law.

In what follows, AM stands for “Atwood machine”. It is an ideal pulley supported by a string. An ideal pulley is massless and changes the direction of the tension but not its magnitude. Two masses are attached to the ends of a massless inextensible string that goes over the pulley.  The tensions in each string segment are equal.  Multi AM assemblies are obtained by replacing masses with pulleys, each with its pair of masses. The label AM-N signifies an assembly with N+1 tiers, $2^N$ masses and $(2^N-1)$ ideal pulleys.  For example, the one in the figure on the right is an AM-2; it has two tiers with pulleys and one tier with masses.  A mass hanging from a ceiling with no pulleys is an AM-0; it has a single tier with one mass.

Three rules

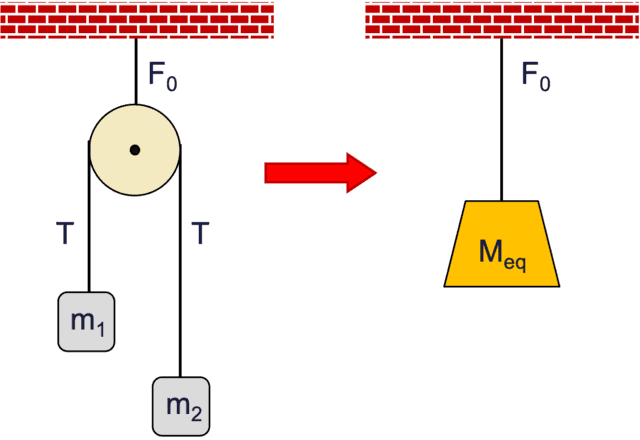
Hanging mass equivalent AM-0 of an AM-1.

We quote without derivation the well-known expression for the tension in an AM-1. $$T=\frac{2m_2 m_1}{m_2+m_1}g.$$ We are seeking a single equivalent mass, $M_{\text{eq}}$, to replace the AM-1 shown in the figure on the right.  In other words, remove the two hanging masses, block the pulley from spinning, and assign mass $M_{\text{eq}}$ to the pulley so that the supporting tension $F_0$ in the string stays the same.  This means that $$\begin{align} & F_0=2T=\frac{4m_1m_2}{m_1+m_2}~g =M_{\text{eq}}^{(1)}~g \nonumber \\
& \implies M_{\text{eq}}^{(1)}=\frac{4m_1m_2}{m_1+m_2}=\frac{4}{\frac{1}{m_1}+\frac{1}{m_2}} \nonumber \\
& \implies \frac{1}{M_{\text{eq}}^{(1)}}=\frac{1}{4}\left(\frac{1}{m_1}+\frac{1}{m_2}\right).
\end{align}$$

Rule I

The pulley and masses in an AM-1 may be replaced by an equivalent mass to form an AM-0. This equivalent mass is equal to four times the product of the masses divided by their sum.  When acted upon by an external force, the acceleration of the equivalent mass will be the same as the acceleration of the pulley in the AM-1 assembly.

Proof
Consider an AM-1 hanging from the ceiling of an elevator with acceleration $A$, a signed quantity.  Let $F$ be the force acting upon the equivalent mass.  Applying Newton’s second law, $$\begin{align} M_{\text{eq}}^{(1)}A=F-M_{\text{eq}}^{(1)}~g.\end{align}$$ We know that the force acting on the AM-1 assembly is $2T$.  To prove Rule I, we need to show that, with the definition of $M_{\text{eq}}^{(1)}$ in equation (1), it follows that $2T=F$.

From Newton’s second law, the accelerations of the masses relative to the lab frame are $$a_1=\frac{T}{m_1}-(g+A)~;~~a_2=\frac{T}{m_2}-(g+A).$$

The constraint that the length of the string connecting the masses be constant demands that the sum of the accelerations be zero. Adding the equations,$$\begin{align} & 0=a_1+a_2=T\left(\frac{1}{m_1}+\frac{1}{m_2}\right)-2g-2A \nonumber \\
& \implies A=T\left(\frac{m_1+m_2}{2m_{1} m_{2}}\right)-g =T\frac{1}{2}\left(\frac{1}{m_1}+\frac{1}{m_2} \right)-g=\frac{2T}{M_{\text{eq}}^{(1)}}-g\nonumber \\
& \implies M_{\text{eq}}^{(1)}A=2T-g.
\end{align}$$Comparison of equation (3) with equation (2), reveals that we must identify $2T=F.~~~~$ Q.E.D.

We conclude that we can replace an AM-1 with an equivalent hanging mass AM-0.  Conversely, we can replace a hanging mass $M$ with an equivalent pulley and two masses to form an AM-1.  The two masses must fulfill equation (1) but there is no unique choice, e.g. $m_1 = m_2=2M;$  $m_1=\frac{3}{10}M, m_2=\frac{3}{2}M$ and so on.

Thus, successive replacements of pulleys by equivalent masses can convert an AM-N  into an AM-0.  This conversion is unique.  Likewise,  successive replacements of masses by equivalent pulleys can convert an AM-0 into an AM-N. This conversion is not unique.

Rule II

The equivalent mass of an AM-N is given by $$\begin{align} \mathbf{\frac{1}{M_{\text{eq}}^{(N)}}=\frac{1}{4^N}\sum_{i=1}^{2^N}\frac{1}{m_i}.}\end{align}$$Proof

The top two tiers of an AM-N form an AM-1.  The top tier is Tier 0. We know that an AM-1 has equivalent mass given by equation (1) $$\frac{1}{M_{\text{eq}}^{(1)}}=\frac{1}{4}\left( \frac{1}{m_{1,1}}+\frac{1}{m_{1,2}}\right).$$ The first subscript denotes the tier number (starting at 0) and the second denotes the position of the mass within a tier, left to right. These two masses are the equivalents of pairs in Tier 2 below. Then $$\begin{align} \frac{1}{M_{\text{eq}}^{(2)}}\nonumber & = \frac{1}{4}\left[\frac{1}{4}\left(\frac{1}{m_{2,1}}+\frac{1}{m_{2,2}}\right)+\frac{1}{4}\left(\frac{1}{m_{2,3}}+\frac{1}{m_{2,4}}\right)\right]\nonumber \\&=\frac{1}{4^2}\left(\frac{1}{m_{2,1}}+\frac{1}{m_{2,2}}+\frac{1}{m_{2,3}}+\frac{1}{m_{2,4}}\right).\nonumber \end{align}$$ The equation above gives the reciprocal of the equivalent mass of an AM-2.

It should be obvious that, when we add another tier and go from Tier $k$ down to Tier $k+1$, we are converting an AM-k into an AM-(k+1). The reciprocal of the equivalent mass of the AM-(k+1) will have twice as many masses added reciprocally multiplied by an additional factor of $\frac{1}{4}$ up front.  Thus, starting with equation (1) for AM-1 one gets the expression for the equivalent mass of AM-2. From the AM-2 one gets the equivalent mass for AM-3 and so on until, after N steps, one reaches equation (4) for the equivalent mass of the AM-N.

Rule III

In an AM-N, the strings that support pulleys or masses in the k-th Tier have the same tension. It is equal to the weight of the equivalent AM-0 divided by the number of strings in the Tier, $\mathbf{T_k=\dfrac{M_{\text{eq}}^{(N)}~g}{2^k}.}$

Proof

Start with an AM-0 hanging from a ceiling.  The tension in the string is $T_0=M_{\text{eq}}^{(N)}~g$. Sequentially transforming this AM-0 into equivalent AM-1, AM-2, . . . , AM-N will, after each step, double the number of strings and halve the magnitude of the tension in each string.   It follows that $T_k=\dfrac{M_{\text{eq}}^{(N)}~g}{2^k}.$

Rule implementation

With the three rules above, finding the accelerations of all the masses in an AM assembly is straightforward.

1. Identify $N$ for the assembly at hand.  It might be necessary to transform masses into equivalent pulleys to keep the bookkeeping simple.  For example, the so-called double Atwood machine has an AM-1 on one side of the top pulley and a mass on the other.  The assembly becomes an AM-2 by transforming the lone mass into an equivalent AM-1.
2. Use equation (4) to find the equivalent mass of the assembly.
3. Use $T_N=\dfrac{M_{\text{eq}}^{(N)}~g}{2^N}$ to find the tension in Tier N.
4. Use Newton’s second law to find the acceleration of each mass relative to the lab frame: $$\begin{align} T_N-m_{N,i} g=m_{N,i} a_{N,i} \implies a_{N,i}=\frac{T_N}{m_{N,i}}-g~~~~(i=1,\dots,2N)\end{align}$$ Note that the acceleration of the i-th mass is positive if the tension is greater than its weight and negative if the tension is less than its weight.  In other words,  the implicit convention is “up” is positive and “down” is negative.
5. If desired, repeat steps 3 and 4 to find the acceleration of the equivalent masses of pulleys in the tiers above.

We see that equal masses in the same tier of an AM-N have equal accelerations regardless of the values of the other masses.  Using equation (5) and the expressions for $T_N$ and $M_{\text{eq}}^{(N)}$, we find that the sum of the accelerations is zero. $$ \sum_{i=1}^{2^N} a_{N,i}  =T_N \sum_{i=1}^{2^N}\frac{1}{m_{N,i}}- \sum_{i=1}^{2^N}g=\frac{M_{\text{eq}}^{(N)}~g}{2^N} \frac{4^N}{M_{\text{eq}}^{(N)}}- 2^N~g =0.$$This is expected because the relative accelerations of masses coupled under the same pulley add to zero and the acceleration of the equivalent AM-0 is zero.

Furthermore, we can find the acceleration of the center of mass. With $M= \sum\limits_{i=1}^{2^N}m_{N,i}$, $$ \begin{align} &\sum_{i=1}^{2^N}m_{N,i} a_{N,i}=\sum_{i=1}^{2^N}T_{N,i}-\sum_{i=1}^{2^N}m_{N,i} g
\implies MA_{\text{cm}}=M_{\text{eq}}^{(N)}g-Mg \nonumber \\ &\implies A_{\text{cm}}=\left(\frac{M_{\text{eq}}^{(N)}}{M}-1\right)g.\nonumber \end{align}$$

Examples

Although the method is conceptually simple, the hierarchical structure of nested equivalent masses makes the explicit formulation of the accelerations in terms of the given masses impractical. It is expedient to set up a spreadsheet in which the arrangement of cells follows the pattern of the AM-N.  Such an arrangement provides a convenient at-a-glance view of the motion.

There are N+1 tiers labeled by $0\leq k\leq N.$ Tier N shows the $2^N$ values of the given masses. Tier N-1 shows the $2^{N-1}$ calculated equivalent masses of the pulleys supporting pairs of masses below. These equivalent masses become “given” masses for Tier N-2 and so on.  Working from the bottom up, one reaches Tier 0 which shows the configuration’s equivalent mass.  This completes the first step of filling in the equivalent masses.

The second step is filling in the tensions supporting each mass. The content of the single cell at the top tier multiplied by $g$ gives the equivalent weight of the AM-N, $F_0$.  Knowing that one moves down tier by tier, halving the tension from the tier above, until one reaches Tier N with the given masses.

The third step is filling in the accelerations.  For each mass, $$\text{Acceleration = Tension divided by mass – Acceleration of gravity.}$$ Accelerations of equivalent masses are, of course, the accelerations of the pulleys they have replaced.

The fourth and final step is filling in the acceleration of each mass relative to its pulley. This step is useful for validating the setup.  Masses (or pulleys) on either side of a pulley above them must have accelerations added to zero by the constraint that lengths of strings passing over pulleys are constant.

AM-2

We are now ready to address the multiple-choice question in the introduction. To find the direction of the angular acceleration of pulley P, we need to compare the equivalent masses of pulleys A and B. Whichever is larger determines the direction of the net torque.

$M_{\text{eq-A}}^{(1)}=4\times\dfrac{1\times 2}{1+2}~\text{kg}=\dfrac{8}{3}~\text{kg}$

$M_{\text{eq-B}}^{(1)}=4\times\dfrac{4\times 0.8}{4+0.8}~\text{kg}=4\times\dfrac{3.2}{4.8}~\text{kg}=\dfrac{8}{3}~\text{kg}$

Since the equivalent masses are equal, they do not accelerate hence the angular acceleration of pulley P is zero.

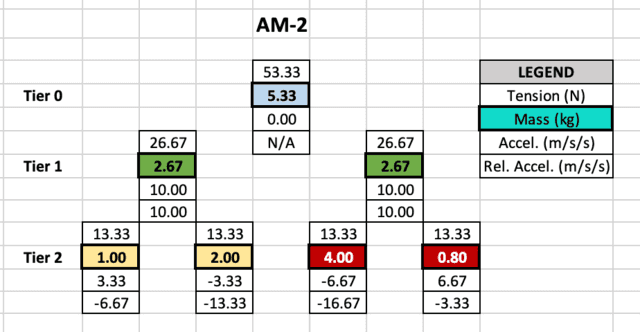The figure on the right shows the spreadsheet output of the AM-2 in the question.

1. Masses are in cells highlighted with color. Masses with the same color belong to the same pulley.
2. The given masses are in Tier 2.  Tiers 0 and 1 show equivalent masses of pulleys.
3. The tension on a mass is one cell above.
4. The acceleration of a mass relative to the lab is one cell below.
5. The acceleration of a mass relative to its pulley is two cells below.

AM-3

Perhaps a more interesting example is an AM-3 with masses selected to illustrate features mentioned earlier. We use double subscript $i,j$ to identify a mass in Tier $i$ at position $j$ from the left.

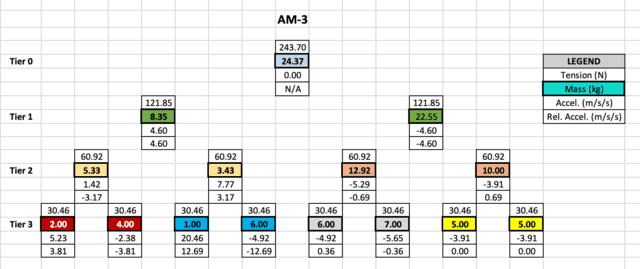
Noteworthy features

1. Accelerations in the same tier add to zero.
2. Relative accelerations of same-color masses add to zero.
3. Masses $m_{3,4}$ and $m_{3,5}$ are equal but not paired under the same pulley. Their accelerations are the same while their accelerations relative to their pulleys are not.
4. Masses $m_{3,7}$ and $m_{3,8}$ are equal and paired under the same pulley.  Their accelerations are equal to the acceleration of their common pulley $m_{2,4}.$ This means that they move as one with the pulley.  It also confirms that if we view $m_{2,4}$ as an AM-0 ignoring $m_{3,7}$ and $m_{3,8},$ the effect on the rest of the assembly will be identical to viewing $m_{2,4}$ as the pulley of an AM-1 with $m_{3,7}$ and $m_{3,8}$ hanging from it.
5. A mass, in this case $m_{3,3}$, may have a positive acceleration greater than $g=10~\text{m/s}^2$. However, no mass can have a negative acceleration relative to the lab frame with a magnitude greater than $g$.  This is consistent with the notion that “you can pull but not push with a string.”

AM-4 and beyond

We can extend the AM-3 above to an AM-4 calculation on a spreadsheet quite easily.

1. Create Tier 4 with the 16 given masses.
2. Replace the old given mass values in Tier 3 with the appropriate equivalent mass formulae.
3. Watch the spreadsheet and recalculate everything.

Calculations beyond AM-4 will probably require abandoning the spreadsheet in favor of code to compact the output. We summarize the equations for an AM-N:

Equivalent mass $$\begin{align}M_{\text{eq}}^{(N)} = \frac{2^{2N}}{{\sum\limits_{i=1}^{2^N} \left(\frac{1}{m_{N,i}}\right)}}.\end{align}$$Tension on any of the $2^{k}$ masses in Tier $k~$ ($0 \leq k \leq N$) $$\begin{align}T_k=\frac{M_{\text{eq}}^{(N)}g}{2^{k}}=\frac{2^{2N-k}}{{\sum\limits_{i=1}^{2^N} \left(\frac{1}{m_{N,i}}\right)}}g.\end{align}$$Acceleration of $j$th mass in Tier $k$ $$\begin{align} a_{k,j}=\frac{T_k}{m_{k,j}}-g=\left[\frac{M_{\text{eq}}^{(N)}}{2^{k}~m_{k,j}}-1\right]g=\left[\frac{2^{2N-k}}{m_{k,j}{\sum\limits_{i=1}^{2^N} \left(\frac{1}{m_{N,i}}\right)}}-1\right]g.\end{align}$$

AM$-{\infty}$

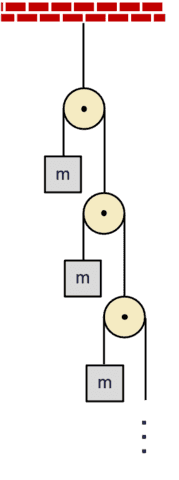The so-called infinite Atwood machine consists of an infinite ladder of pulleys each with mass $m$ on one side and a pulley on the other (see figure on the right).  Of interest are the accelerations of the masses $m.$

Let $M_{\text{eq}}^{(\infty)}$ be the equivalent mass of the entire assembly, i.e. the equivalent mass of the AM-0.  Consider the AM-1 equivalent of the assembly. Its single pulley has mass $m$ on the left and $M_{\text{eq}}^{(\infty)}$ on the right.  The equivalent mass of this AM-1 is $M_{\text{eq}}^{(\infty)}$.  Thus, $$M_{\text{eq}}^{(\infty)}=\frac{4mM_{\text{eq}}^{(\infty)}}{m+M_{\text{eq}}^{(\infty)}}\implies M_{\text{eq}}^{(\infty)}=3m.$$ Then,$$\begin{align} & T_1=\frac{1}{2}M_{\text{eq}}^{(\infty)}~g=\frac{3}{2}mg\implies a_1=\frac{T_1}{m}-g=\frac{3}{2}g-g=\frac{1}{2}g \nonumber \\ & T_2=\frac{1}{4}M_{\text{eq}}^{(\infty)}~g=\frac{3}{4}mg\implies a_2=\frac{T_2}{m}-g=\frac{3}{4}g-g=-\frac{1}{4}g \nonumber \\ &\dots \nonumber \\ & T_N=\frac{1}{2^N}M_{\text{eq}}^{(\infty)}~g=\frac{3}{2^N}mg\implies a_N=\frac{T_N}{m}-g=\left(\frac{3}{2^N}-1\right)g \nonumber \\&\dots \nonumber \\ \end{align}$$Only the topmost mass $m$ has acceleration up. The rest of the accelerations are down approaching free fall as $N\rightarrow\infty.$

Afterthoughts

There is enough resemblance between the reciprocal mass addition in equation (1) and the expression for equivalent capacitance in a series combination to make one wonder whether there is an electrical analog for an AM-N.  I suspect there is but, to keep this story short, I will save the idea for a separate article.

I should also note that Atwood machines replacing hanging masses in standard problems can make a simple situation appear complicated.  For example, attach an AM-N to a vertical spring and set it into oscillations. The oscillation frequency is, of course, $\omega=\sqrt{k/M_{\text{eq}}^{(N)}}.$ The acceleration of the equivalent mass has the form $A(t)=-\omega^2x_0\sin(\omega t+\phi).$  A separate AM-N calculation, following the methods outlined here, yields the acceleration of the masses $a_{AM,i}$ relative to a fixed support. By Rule I, the accelerations of the hanging masses relative to the lab frame will be  $a_i(t)=a_{AM,i}-A(t).$

This article was inspired by a recent homework problem.  I hope that the simplicity of the method will encourage the reader to adopt the equivalent mass approach instead of FBDs or Lagrangians when treating multiple Atwood machine problems.  Quoting David J.  Griffiths in his textbook Introduction to Quantum Mechanics quoting Peter Lorre in the film Arsenic and Old Lace, “Do it ze kveek vay, Johnny!”