Introduction to Electric Vector Potential and Its Applications

Main Point: The electric vector potential offers a  means of determining the non-conservative component of mixed stationary or quasi-stationary electric field

While many are familiar with the static magnetic vector potential

$\bf A = (\mu/4\pi) \int \bf j~ dv/s$

with $\bf j$ = current (area) density within differential volume $dv$ and $s$ = distance from $dv$ to the point of observation,  the magnetic field is then derivable from

$\bf B =  \nabla \times \bf A$.

However, finite vector potentials exist in any vector field $F$ for which $\nabla \times \bf F \neq 0$.  If the field is wholly scalar  the vector potential is zero.

The Helmholtz decomposition theorem can be reduced for any electric field to stating that there are two kinds of E field, one for which $\nabla \times \bf E = 0$ (a “scalar” field $E_s$), and the other for which $\nabla \times \bf E \neq 0$, a non-conservative field $E_m$.  An E field can comprise both kinds of field and we call that a mixed field: $\bf E = \bf E_m + \bf E_s$.

The vector potential can serve as a means of identifying the  $\bf  E_m$ part of any static or quasi-static mixed E field at any observation point.  By doing so it ipso facto identifies both the irrotational and non-conservative components at that point.

In fact, a good name for the electric vector potential is “$E_m$ detector.”

The generalized vector potential for a stationary or quasi-stationary field $\bf F$ obeys

$\bf F = -\nabla U + \nabla \times \bf W$

where the scalar potential is $U$ and the vector potential is $\bf W$.

We also know from mathematics that

$\nabla^2 \bf W = -\nabla (\nabla \cdot \bf W)~ – \nabla \times (\nabla \times \bf W)$

For our vector potential $\bf W$ we are however free to choose $\nabla \cdot \bf W = 0$ (by gage invariance or direct verification). Then

$-\nabla^2 \bf W = \nabla \times \bf F$

which are of course 3 scalar equations, one of which is

$-(\nabla^2 W)_z = (\nabla \times \bf F)_z$

and by similarity to the known expression for scalar electric potential

$U = (1/4\pi)  \int \rho/\epsilon~ dv/s$

if we replace $\rho / \epsilon$ with $(\nabla \times \bf W)_z$

we obtain the general relation for a vector field $\bf F$ with vector potential $\bf W$ as

$\bf W = (1/4\pi) \int (\nabla \times \bf F)~ dv/s.$

and $\bf F = \nabla \times \bf W – \nabla U$.

But for an electromagnetic E field we also know that $\nabla \times \bf E  = -\partial \bf B/\partial t$ so we have the electric vector potential $\bf W$:

$$ \bf W = (1/4\pi) \int (-\partial \bf B/\partial t) ~dv/s $$,

with  $\bf E_m = \nabla \times \bf W$  and  $\bf E_s = -\nabla U$.

As a simple example let us apply this formula to a circular B field of infinite length $-\infty < z < +\infty$, cross-sectional area $a$ so flux $\phi = aB$. .  We seek the E field outside the B field.  We then all know a priori that in cylindrical coordinates

$\bf E = -(\partial \phi/\partial t)/2\pi~ r ~ \hat {\bf \theta}$

forming circles of radii r.

By the electric vector potential on the other hand,

$\bf W = (1/4\pi) \int (\nabla \times \bf E)~dv/s$

$= -(1/4\pi) \dot B\int dv/s.$

We have $dv = a ~dz$

$\phi = aB$

$s = (z^2 + r^2)^{1/2}$, so

$\bf W = W_z \hat {\bf k}$ since  $\bf W$ is in the direction of $\bf B$

$W_z(r,d)  =~ – (1/4\pi) \dot \phi \int_{-d}^d ~ dz/(z^2 +r^2)^{1/2}$

$W_z(r,d) = ~ – (1/4\pi) \dot \phi ~~ \ln~ \frac {(z^2 + r^2)^{1/2} + z} {(z^2 + r^2)^{1/2} – z}$ evaluated   (z= d) – (z= – d).

Now $\bf E = \nabla \times \bf W$ or

$E_{\theta} =  lim ~  d \to \infty$  of $\partial {W_z(r,d)}/\partial r$

$=~ – (1/4\pi) \dot \phi   ~~ lim ~~d \to \infty of  2d/r(r^2+ d^2)^{1/2}$

$= ~- \dot \phi/2\pi~r$

i.e. the answer we knew beforehand.

****************************************************************************

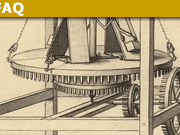
Now, to some folks’ annoyance, I will again put a resistive ring concentric with a time-varying B field of infinite extent at radius $a$.  Assume first a uniform ring of resistance $r$.  The formula gives the same answer as without the ring: $E_m = -\partial \phi/\partial t/2\pi a$  all around the ring.

Now assume half the ring has resistance $r$ and the other half $2r$.  See fig. 1:

Fig. 1 Non-uniform resistive ring surrounding time-varying B field

 

The electric vector potential formula still gives the same answer $E_m$, as it should.

But, but – we can readily determine via Faraday’s and Ohm’s laws that the $r$ side has half the E field of the $2r$ side.  What gives?

The truth, inconvenient though it may be, is in my last blog: the fields are a mixture of scalar and non-conservative fields.

The electric vector potential finds only the part of the E field ascribable directly to the time-varying B field, in other words the $E_m$ part. (The electrostatic part $E_s$ is of course $-\nabla U$ for the two equal & opposite $E_s$ fields.

Cf.

https://www.physicsforums.com/threads/how-to-recognize-split-electric-fields-comments.984872/

Now, one may wonder why bother with identifying split fields when most measurable parameters (voltmeter readings, joule heating, current, net E field, plus obeyance to Faraday’s law etc.) can all be found by assuming just one kind of E field?

My answer is twofold:

(a) the E fields inside and outside the ring are greatly affected by the free charges setting up the $E_s$ fields. In Fig. 1, net positive free charge accumulates at A with an equal negative charge at B.  (With the uniform ring there are no free charges, thus no impact on the fields.  It’s just the same $E_m$ as if there were no ring, with  $E_s = 0$.)

These field changes are not appreciable without an understanding of split fields.

(b) are we physicists or technicians?  Do we want to know what’s really going on or not?

I am reminded of the ring laser gyro: the true explanation for the phase shift as a function of rotation rate can only be provided by relativity, i.e. the Sagnac effect.  Yet we get exactly the same phase shift by ignoring relativity altogether, by simply adding the speed of rotation to the speed of light, Galilean style.  So should we ignore the Sagnac effect and relativity?

Final note: the electric vector potential is more powerful than the faraday rule $\oint \bf E \cdot \bf {dl} = – \partial \phi/\partial t$ since the faraday formula does not distinguish between electrostatic and emf-generated E fields, while the vector potential gives a point-by-point accurate reading for the emf part of the field around any closed loop.  The rest must be electrostatic, by Helmholtz.

http://farside.ph.utexas.edu/teaching/em/lectures/node37.html

Comment Thread