How to Scientifically Measure How Many Days Are in a Year

Days in a Year Summary

• The article explores the measurement of the number of days in a year, considering various definitions of a “day” and a “year.”
• It starts with the common knowledge that a year has 365 days, with leap years having 366 days.
• The concept of a “stellar day,” based on Earth’s rotation concerning fixed stars, is introduced.
• The “sidereal year,” the time it takes for Earth to orbit the Sun concerning the stars, is discussed, revealing a slightly longer duration than previously thought.
• Differences between stellar and 24-hour days are attributed to the Earth’s elliptical orbit and its effect on solar day length.
• Precession, the wobbling of the Earth’s axis, is explained as causing long-term changes in star positions and the Sun’s location.
• The article summarizes various measures of a year, including the tropical year and anomalistic year, and their relationship to Earth’s motions.

How many days are there in a year?

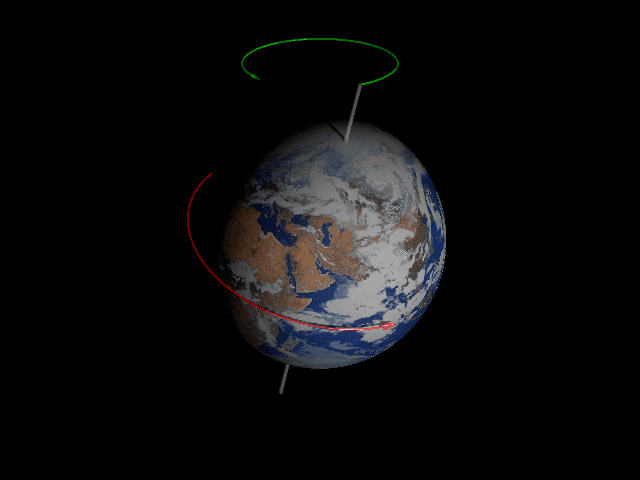
Ask pretty much anyone and they will tell you 365, except for leaps years which have 366. In addition, most people can tell you that a year is the amount of time that it takes for the Earth to go once around the Sun, and a day is the amount of time it takes for the Earth to rotate on its axis once. (I say “most”, because, in a survey done too long ago, only 74% of Americans surveyed even knew that the Earth went around the Sun.) Given the fact that leap years occur every four years (with exceptions), it turns out that the Earth rotates ~365.25 times for every trip it makes around the Sun, so you could say that there are ~365.25 days in a year. (The Julian calendar assumed that there were 365.25 days in the year and added a leap year every four years to account for that extra ¼ of a day. And while the Julian calendar has since been replaced with a more accurate one, astronomers still use Julian dates in many of their calculations. The light-year is the distance light travels in a Julian year.)

However, the above definitions of “day” and “year” are a little vague. One trip around the Sun and one rotation on the Earth’s axis, concerning what? The reference often used by astronomers is that of the “fixed” stars. If we measure one rotation of the Earth concerning the stars we call it a “stellar day”. Using the same reference, one trip of the Earth around the Sun concerning the stars is called a “sidereal year”, from the Latin word “sidus” meaning star. (from this you would think that a rotation of the Earth concerning the stars would be called a sidereal day, but oddly, a sidereal day is measured concerning a different reference which we will deal with later on.)

If you measure the Earth’s rotation concerning the stars you get 86164.098903691 seconds per rotation, and if you do the same for the Earth’s orbit around the Sun, you get 31558149.76… sec. This means that, concerning the stars, the Earth rotates 366.25636623 times while it orbits the Sun once. This means that there are 366.25636623 stellar days to the sidereal year This is at least one whole “day” more than the 365.25 we came up with earlier. So where does this difference come from?

You may have noticed that the length of a stellar day differs from what we normally consider as a day of 24 hrs, with 60 min hrs and 60 sec minutes which works out to 86400 sec, and is almost 4 minutes longer than the stellar day. This is because our 24-hour clock is based on the “Solar day”, or the time it takes for the Sun to go from noon on one day to noon on the next, and this period is affected by the Earth’s orbit around the Sun.

The Stellar vs. Solar Day

In the time it takes the Earth to make one rotation concerning the stars, the Earth travels a bit under 1 degree around the Sun. So a spot that starts directly under the Sun will not be so 1 stellar day later.

This means that the Earth must continue rotating a bit longer (~ 4 min) to finally return to that spot directly under the Sun. So it turns out that 1 solar day equals 1.002737803 stellar days.
( The length of the solar day worked out above is for the “mean” solar day. The Earth does not orbit the Sun in a perfect circle but in an ellipse. Because of this, its orbital and angular speed around the Sun varies over the course of its orbit. It travels faster near perihelion and slower at aphelion. This makes the solar days when the Earth is near perihelion longer than those when we are near aphelion. At present, perihelion occurs in December, so this is when the longest solar days occur. So for those of you in the Northern Hemisphere who feel that Winter days seem to drag on while Summer days fly by, you are not entirely incorrect. This will not always be the case, however, as we will learn later.)

One of the side effects of this difference between the stellar and solar day is that the stars that we see in the night sky change over the course of a year. The Winter night sky will be different from the Summer night sky. In addition, if we could see the stars during the day, the constellation that we would see the Sun in also changes over the course of the year. (This is the basis of astrology. The Sun passes through twelve constellations which are the “signs” of the Zodiac in a year. The constellation in which the Sun is in on your birth date is your Sun sign.)

Sun’s position in Taurus on May 21, 2015

So now we can work out that there are 365.2563662 mean solar days to a sidereal year, which is slightly more than the 365.25 days per year we estimated earlier.

This means that if you wished to create a calendar that kept step with the sidereal year, you could start with the Julian calendar and then “fudge” it to make it more accurate

The Gregorian calendar is a result of fudging

The Gregorian calendar is accurate to within 1 day in several thousand years when it comes to keeping the calendar in step with the seasons (The aim of most calendars). To accomplish this, leap days were eliminated on century years that were not evenly divisible by 400. (1900 was not a leap year, but 2000 was.) So every 400 years there are 97 leap days added for a total of 146097 days vs 100 leap days for a total of 146100 with the Julian calendar.

But hold on. With 365.2563662 days to a sidereal year, in 400 sidereal years, you end up with 146102.5465 days or over 5 days more than accounted for by the Gregorian calendar and 2.5465 days more than accounted for by the Julian calendar. This means if we want to keep step with the sidereal year, then the Julian calendar is a better fit than the Gregorian calendar and in order to make it an even better fit, we would have to add more leaps years not fewer.

Gregorian year vs sidereal year

The reason is that the sidereal year and the seasons do not keep in step.

To understand why this is, we need to look into what causes the seasons, and this is the tilt of the Earth’s axis concerning the Sun.

When the Northern hemisphere leans toward the Sun we have Summer, and when the Northern hemisphere leans away from it we have Winter. The moment the Northern hemisphere is inclined at its greatest to the Sun is called the Summer solstice and when it is inclined away by the greatest amount, it is called the Winter solstice. The Autumn and Spring (or Vernal) equinoxes are when the tilt is neither towards nor away.

The Northernmost line of latitude where the Sun can be directly overhead (during the Summer Solstice) is called the Tropic of Cancer. (so-called because astrologically speaking, the Sun sign at this time is Cancer.) The Southernmost line of latitude where the Sun can be directly overhead during the Winter solstice is the Tropic of Capricorn, so named for the same reason.)

The time period between Vernal equinoxes is called a tropical year. Because during this period the Sun goes from being directly overhead the equator at noon to overhead the Tropic of Cancer, to over the equator, to over the Tropic of Capricorn, and finally back to the equator again. This is also the seasonal year and so the Gregorian calendar is designed to fit the tropical year.

Now if this were all there was to it, and the Earth’s axis always pointed in the same direction with respect to the stars, the seasons would keep in step with the Earth’s trip around the Sun and the tropical year and sidereal year would be equal in length. But as we saw above, this isn’t the case.

The truth is that the Earth’s axis doesn’t stay fixed with respect to the stars; It “wobbles” like a spinning top. This wobble is called precession.

A spinning top precesses because it is trying to fall over. Gravity pulls on it and applies torque to the axis of rotation. The top, in turn, tries to preserve angular momentum, and the torque is converted to a precession of the axis.

With the Earth, gravity is the culprit also, Both the Sun and Moon (and the other planets to a certain degree) exert a gravitational effect on the Earth, each pulling on the far side a little less than the near side. If the Earth was perfectly spherical, this would not matter, but the Earth is a slightly oblate spheroid. The effect of this gravitational difference across the Earth is that both the Moon and Sun exert a torque on the Earth which tries to align the equatorial bulge with the planes of the respective orbits. The combined torque exerted by both these bodies has the same effect as the gravity trying to topple over the spinning top and causes the spinning Earth to precess.

The resulting precession causes the Earth’s axis to trace out one complete circle with respect to the stars every 25770 years. This means if you started with the Northern hemisphere leaning towards the Sun, after the 12885 sidereal years, the Earth’s axis will also have precessed ~180 degrees with respect to the stars and you will have the Northern hemisphere leaning away from the Sun after those 12885 sidereal years.

Thus with a calendar based on the sidereal year, the seasons would slowly drift with respect to the calendar, and you’d eventually have Summer weather occurring in December. The end result is that the tropical year is slightly shorter than the sidereal year, being 365.24219 mean solar days long vs. 365.2563662 mean solar days to a sidereal year. 365.2563662 times 400 equals 146096.876, which is very close to the 146097 days in the Gregorian calendar for the same period, which is why it is such a better fit.

This difference of 0.0141762 days per year also leads to what is known as the precession of the equinoxes. If we compare the relative position of the Earth at the Vernal equinox with respect to the stars, we find that it changes over time.
(And this is why we have both a sidereal and stellar day as I mentioned earlier; the sidereal day is measured with respect to the Vernal equinox and the stellar with respect to the stars, making the sidereal day slightly shorter than the Stellar day)

Further, this means that not only does the night sky change day by day, it also changes over the years. On any given date, the night sky changes slightly from year to year. It isn’t much and isn’t noticeable from one year to the next, but throughout an average person’s lifetime, it works out to be a shift of a bit over twice the width of the full Moon.

This also means that the position of the Sun with respect to the stars on a given date as seen from the Earth also changes over the years. In the time since the dates for the astrological signs were established, the Sun has moved an entire Zodiac sign. Thus, during the Summer solstice this year, instead of just entering Cancer as the astrological dates suggest, the Sun is just leaving Taurus and entering Gemini. (So if the Tropic of Cancer had been named today, it would have likely been called the Tropic of Gemini and the Tropic of Capricorn would be the Tropic of Sagittarius).

So if you wanted to keep the astrological signs in step with the constellation the that Sun is in on a particular day, you would need to shift the dates of the astrological sign by 1 day every 68 years or so. ( Another indication of the silliness of astrology, as it does not even keep consistent with its original premise that the sign(constellation) the Sun is in on the day you were born determines your personality.)

Answering “How many days are in a year?”

Considering the 2 different “years”, sidereal and tropical, and 3 different “days”, stellar, solar, and sidereal a list comparing them all would look like this.

• 365.24219 solar days to a tropical year
• 365.256363009 solar days to a sidereal year
• 366.2421544183 stellar days to a tropical year
• 366.2421900073 sidereal days to a tropical year
• 366.2563662303 stellar days to a sidereal year
• 366.2564018207 sidereal days to a sidereal year

The Shifting Perihelion

Remember earlier when I mentioned that perihelion of the Earth’s orbit occurred in December and that this made Winter days longer? I also said that this will not always be the case. Here’s why:

I already mentioned that the Earth does not orbit in a perfect circle but in an ellipse, with a perihelion and aphelion. The time it takes for the Earth to go from perihelion to perihelion is an “anomalistic year” (because the angular distance between a planet and its last perihelion is called the anomaly). Because the Earth’s orbit is subject to the gravitational tugs of other bodies in the Solar system, it undergoes a precession so that the perihelion shifts a bit over time with respect to the stars. Thus the time it takes for the Earth to go from perihelion to perihelion is just a bit longer than a sidereal year, which in turn is longer than a Tropical year, making the anomalistic year 365.259636 mean solar days long.

This also means that the perihelion date changes slightly from year to year, or by about 1 day every 57 years.
So for those of you lamenting those long Winter days in the Northern Hemisphere, take heart, in 10,000 years or so they will be a bit shorter as the perihelion shifts to the Summer months.

Next: Here Be Dragons.