Misconceiving Mutual Inductance Coefficients

 

A commonly used formula for mutual inductance M between two nearby coils L1 and L2 is M = k√(L₁*L₂). This formula however assumes equal percentage flux linkages between the two coils. This requirement is often omitted in several of the references I have looked at.

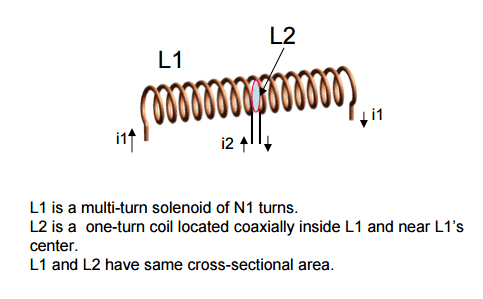
That this requirement is not necessarily met can be seen by looking at fig. 1, which depicts a single-turn coil L2 embedded within a long solenoid L1 with N₁ turns. It is obvious that flux from L1 essentially totally links L2, whereas flux from L2 equally obviously is coupled only partially into L1.

 

Some nomenclature:
φ₁₁ = flux generated by L1 coupling into itself;
φ₂₁ = flux generated by L1 coupling into L2;
φ₁₂ = flux generated by L2 coupling into L1;
φ₂₂ = flux generated by L2 coupling into itself.

So mutual inductance M₂₁ = φ₂₁/i₁ (N₂ = 1 here); and
M₁₂ = N₁φ₁₂/i₂.
Also,
L₁ = N₁φ₁₁/i₁ and
L₂ = φ₂₂/i₂.

 

As is well known, M₂₁ = M₁₂ = M. (The proof is not trivial; Feynman uses the magnetic vector potential while Skilling invokes an energy argument.)

The following fallacious reasoning can ensue, and I speak from experience! So M can be computed either way per the above. Obviously, it’s much easier to go with M₂₁ since φ₂₁ = φ₁₁ . I won’t derive the result, which is easily done and is M = μ₀A/l in a vacuum
where A = cross-sectional area of both coils and l = length of L1.

So now we say OK, there is 100% flux coupling between L1 and L2 so k = 1 and M = the (too!) familiar k√(L₁L₂). WRONG!

Were it right we could do an amazing thing: we could easily compute L₂ which otherwise happens to be an exceedingly difficult task; L₂ depends on A and the wire radius R and can only be derived from a special integral to some arbitrary order. But – we know L₁, we know M and we think we know k so L₂ can easily be computed!

Not so! The result of this fallacious computation would imply that L₂ is a function of L₁, even in the total absence of solenoid current i₁! And you could also ignore little inconvenient realities like L₂ → ∞ as R → 0!

The thing is, there are really two coupling coefficients. Define
k₁ = φ₂₁/φ₁₁ and
k₂ = φ₁₂/φ₂₂. Then we can perform a few substitutions based on the above to find that
M = √(k₁k₂L₁L₂).

The bottom line here is that we know k₁ but not k₂, and L₁ but not L₂. There is one coupling coefficient k = k₁ = k₂ if and only if the fraction of flux from one coil coupling into the other is the same for both coils.

Even if the single-turn coil were replaced by another long solenoid _L2, but of different length, wrapped on top of L1 so that A is the same for both, and L₂ were as easily computed as L₁, still there are two different coupling coefficients involved, and the familiar formula L₂/L₁ = (N₂/N₁)² is incorrect.

 

Read my next article: https://www.physicsforums.com/insights/brachistochrone-subway/