A Poor Man’s CMB Primer: Orientation of the Universe

 

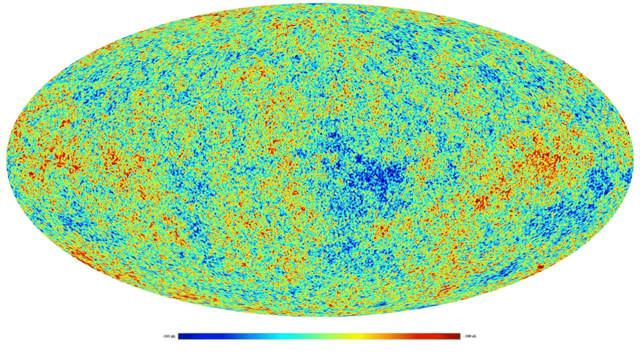
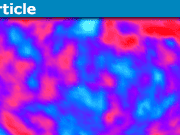
This is a picture of the cosmic microwave background:

Fig 1. The cosmic microwave background as seen by the European Space Agency’s Planck satellite, 2013.

If the universe is an 80-year-old man, here it is as a zygote only a tenth of a second old. It is the oldest light ever observed, and it tells an amazing story.

This picture tells us that the universe is 13.8 billion years old and that it is very flat and exceedingly smooth. It tells us that around 4% of the universe is made of ordinary atoms and that the rest of it is something entirely more exotic. From this picture we know that the universe is expanding and that it’s been doing so at an ever-increasing rate since the formation of the Earth; it tells us that stars first blinked 150 million years after the big bang (or, in keeping with our analogy, around the time the infant universe is finally beginning to sleep through the night.) We know from this picture that the universe lacks perfect symmetry—it’s a tad lopsided with one side warmer than the other. This picture lends impressive evidence for an ultra-rapid period of expansion known as inflation, a growth spurt that in a flash increased the size of the universe a billion billion billion-fold, while simultaneously sewing the tiny quantum seeds that would later grow into clusters and superclusters of whirling galaxies. All of that is from this one picture.

These facts are woven throughout the tiny false-colored bumps and speckles: red for warmer spots, blue for colder. Though striking to the eye, these temperature variations are tiny: they differ by only about 1 part in a hundred thousand. This is a picture of a remarkably uniform field of radiation, with only tiny departures from perfect homogeneity. These tiny and delicate bumps are a cosmic code holding the answers to big and far-reaching questions about the universe, and cosmologists have just about cracked it.

In this set of notes, we will explore the physics of the cosmic microwave background, including its origin, structure, and evolution. We will spend most of our time fixated on the tiny bumps: where they come from, how we analyze them, and what they tell us about the early universe. This is a Poor Man’s Primer, meaning that it strives to be unsophisticated, favoring conceptual clarity over mathematical pedantry. That’s not to say we’ll be pulling our punches, but it does mean we’ll be choosing them carefully.

First, I need to tell you what, exactly, you’re looking at in Figure 1. We need to understand what this is a picture of before we can appreciate what it means.

Orientation

To understand this picture, we first need to appreciate a couple of things about the early universe. The cosmic background radiation was created when the universe dropped below the temperature at which neutral hydrogen can be stably formed (we’ll talk about this process in the next post). Before this time, photons and charged particles existed together as a tightly coupled plasma¹. The universe was opaque, as frequent collisions between the photons and charged matter kept all the light bound up in the plasma. When neutral hydrogen formed, the photons were liberated from this game of billiards: they decoupled and free-streamed across the universe. Traveling across vast stretches of space and time, these photons reach Earth today older and wiser. Once hot, the journey across the expanding universe has sapped their energy, and so they arrive on Earth in the microwave band of the electromagnetic spectrum. These photons are what we call the cosmic microwave background or CMB.

Where you might ask, is the CMB? It’s everywhere! (Let me explain.) When the background radiation decoupled, it was spread more or less uniformly throughout the universe. Suppose we have an observer O who happens to be alive in the universe at the time of decoupling. If he could see these photons (he can’t—they’re in the infrared part of the spectrum, but let’s suppose), what would it look like?

Consider a two-dimensional analog universe, pictured schematically below:

Fig 2. Two-dimensional schematic of the appearance of the cosmic microwave background to an observer situated at O.

Photons arrive at O‘s position from all directions, traveling at the speed of light. At each instant in time, O sees photons that originated from an equidistant collection of points; at early times after decoupling, O receives photons appearing to have originated on the red circle (left panel). The light gray region indicates the points of origin of all photons that have already reached and passed O; the photons coming from the dark gray region have yet to reach him. As time passes (right panels), the red circle grows as photons from further and further outreach O. The grid marks to track the expansion of the universe although we can ignore any expansion for now. And that’s it: from the moment of decoupling to the present day, photons continue to reach O from ever more remote regions of the universe, as the red circle expands outwards at the speed of light. Today, these photons make up the cosmic microwave background that we observe here on Earth.

Returning to our real, three-dimensional universe, the locus of points is not a circle but a sphere. At any given instant, the CMB appears to us on Earth to originate from the inside surface of a large globe with the Earth at the center, called the surface of the last scattering:

Fig 3. To us on Earth, the CMB appears to originate from the inside surface of a large sphere with Earth at the center. Not to scale (obviously).

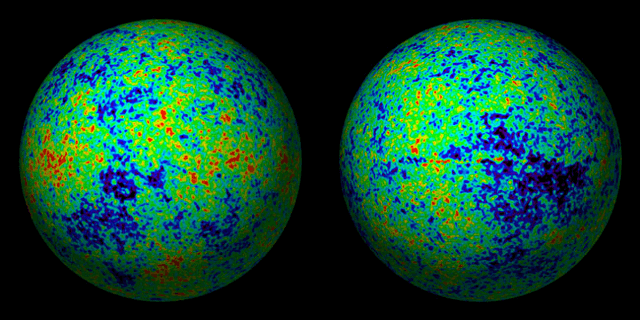
With the help of a whole host of balloon-borne, space-, and ground-based telescopes, over the past two decades, cosmologists have succeeded in measuring the CMB in striking detail. The result of these measurements is a representation of the CMB “sky” as the surface of this sphere: Figure 4 depicts two hemispheres of the CMB globe as seen by NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) in 2003:

Fig 4. A complete representation of the cosmic microwave background divided into two hemispheres.  NASA, WMAP (2003).

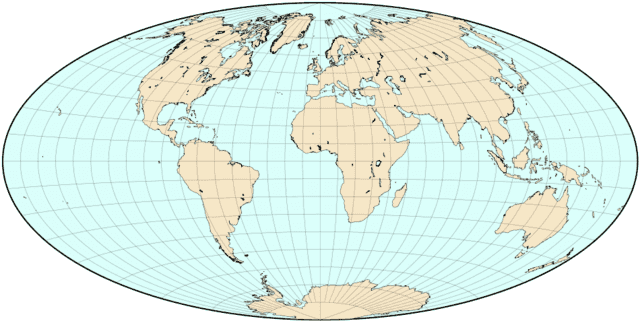
To go from Figure 4 to a map like Figure 1 we need to make some kind of a projection. You are likely familiar with the use of the Mercator projection to represent the curved surface of the earth on a flat surface, like a map. In the Mercator projection, the globe is “flattened” out onto the inner surface of a cylinder. To create CMB maps, the slightly more involved Aitoff projection is employed. The Aitoff projection is useful because it preserves all directions from the central point of the projection. For example, if you center the projection at, say, New York City, then the map accurately depicts the directionality from New York City to all other points on the globe (the Mercator projection lacks this property; according to a Mercator map, as long as I head in a vaguely southerly direction from New York City I’m guaranteed to hit Antarctica, which is spread out across the entire bottom of the map.) Figure 5 depicts what the Earth looks like under an Aitoff projection.

Fig 5. Aitoff projection of Earth. Directionality from the central point of the projection is preserved.

This is what Figure 1 is for the case of the CMB. To summarize the process: you are sitting on Earth at the center of a big sphere that is the CMB sky. Cut it open from, say, the north to the south celestial pole, and then very carefully flatten it out ensuring that the Aitoff condition holds. You’ll end up with Figure 1. It is the whole of the CMB sky, and although it looks a bit distorted, all the information on the original map is retained.

Next time, we’ll take a closer look at how the cosmic background radiation manages to escape from the baryon-photon plasma.

Footnotes

¹Called the baryon-photon plasma, but of course, there were charged leptons in there too. It’s a confusing piece of terminology. back

Click For Forum Comments