Presenting a Rare Kinematic Formula

Here we present some useful kinematic fact which is uncommon for textbooks in mechanics.

Consider a convex rigid body (RB) rolling without slipping on a fixed plane. (The plane can actually be replaced with a some other  fixed surface.)

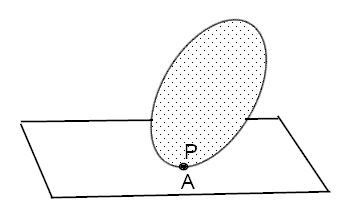
In the picture RB is a filled with dots oval .  At a given moment of time RB contacts with the plane by a point $P$. The point $P$ belongs to RB.  So  in different moments of time we denote by  $P$  the different points of  RB. Let $A$ stand for the point of contact, the point $A$ draws a curve on the plane as RB rolls.

Theorem

$\boldsymbol a_P=-\boldsymbol\omega\times\boldsymbol v_A.$

Here $\boldsymbol a_P$ is the acceleration of the point $P$; $\boldsymbol v_A$ is the velocity of the point $A$; $\boldsymbol\omega$ is the angular velocity of RB.

Proof

Introduce a coordinate frame (say  $Oxyz$) which is connected with RB. With respect to this frame we will consider relative and transport velocities and accelerations. By well-known formula we have

$$\boldsymbol v_A=\boldsymbol v_A^e+\boldsymbol v_A^r,$$ where by superscripts $e,r$ we denote transport velocity and relative velocity respectively. Since RB does not slip it follows that $\boldsymbol v_A^e =0$ and thus

$$\boldsymbol v_A=\boldsymbol v_A^r.\qquad (**)$$

Differentiate the last equality in time

$$\boldsymbol a_A=\frac{\delta}{\delta t}\boldsymbol v_A^r+\boldsymbol \omega\times \boldsymbol v_A^r=\boldsymbol a_A^r+\boldsymbol \omega\times \boldsymbol v_A^r,\qquad (*)$$

here $\frac{\delta}{\delta t}$ stands for derivative relatively the frame $Oxyz$. On the other hand there is  standard formula

$$\boldsymbol a_A=\boldsymbol a_A^r+\boldsymbol a_A^e+2\boldsymbol \omega\times \boldsymbol v_A^r.$$

Observe that $\boldsymbol a_A^e=\boldsymbol a_P$ and by formula (**) we obtain

$$\boldsymbol a_A=\boldsymbol a_A^r+\boldsymbol a_P+2\boldsymbol \omega\times \boldsymbol v_A.$$

Combining the last formula with (*) we get the assertion of the theorem.

As an example of  application of this theorem we just quote  the following classical problem.

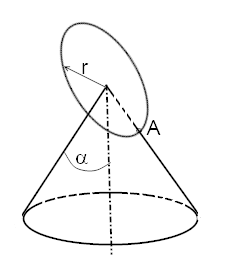
Consider a fixed cone with angle $\alpha$. A disk rolls around the cone without slipping such that   the center of the disk coincides with cone’s apex all the time.  The disk’s rim touches the cone in a point $A$. The point $A$ belongs to the disk. The radius of the disk equals $r$.

Let $a_A$ be a given acceleration of the point $A$ at a moment $t=t_0$.  Find an angular velocity of the disk at the moment $t_0$.