Science and Math Tutorials

Here contain the expert tutorials for all science and math disciplines.  This is a master list. Tutorials are technical and focus on one narrow skill. It’s more like a how-to than a guide.

Brachistochrone

Explaining the General Brachistochrone Problem

/
3 Comments
Consider a problem about the curve of fastest descent in the following generalized statement. Suppose that we have a Lagrangian system $$L(x,\dot x)=\frac{1}{2}g_{ij}(x)\dot…
integralmisconceptions

Some Misconceptions on Indefinite Integrals

/
40 Comments
Integration is an incredibly useful technique taught in all calculus classes. Nevertheless, there are certain paradoxes involved with integration that…
basickinematics

Learn Basic Kinematics in Classical Mechanics

/
8 Comments
There is an interesting thing in teaching of Classical Mechanics. Several theorems which presented below form a core part of kinematics for all Russian…
kinematics

Presenting a Rare Kinematic Formula

/
1 Comment
Here we present some useful kinematic fact which is uncommon for textbooks in mechanics. Consider a convex rigid body (RB) rolling without slipping…
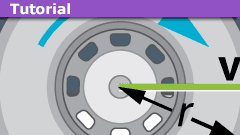
angularvelocity

Elementary Construction of the Angular Velocity

/
1 Comment
Physics books seldom contain an accurate definitions of the angular velocity of a rigid body. I believe that the following construction is as simple as…
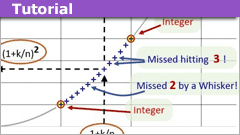
irrationalnumbers

Mathematical Irrationality for Dummies

/
13 Comments
On one of my restless wanderings around the Internet, I came upon a collection of proofs of the statement that the square root of 2 is an irrational…
physics_vectors

Frequently Made Errors in Vectors – Elementary Use

/
2 Comments
 A vector has magnitude and direction. Pictorially, a vector can be imagined as a location in n-dimensional space relative to some fixed origin. …
lightcone7_3

LightCone 8 Tutorial Part III – How Things are Computed

/
1 Comment
In Part I and Part II of this mini-series, we have briefly discussed the basic user interface and the use of charts to depict the LCDM cosmological model.…
complexexponents

Learn Complex and Irrational Exponents for the Layman

/
5 Comments
This Insight is part of our "Young Authors" series, where talented young students showcase their knowledge.  This is how both you and I learned…
computermath

Why Can’t My Computer Do Simple Arithmetic?

/
46 Comments
https://www.youtube.com/watch?v=yYSlcBghLZMThe first computer I owned was an Apple IIe computer, with a CPU that ran at slightly over 1 Megahertz…
lightcone72

LightCone8 Tutorial Part II – Charts

/
3 Comments
Part I dealt with the basic user interface of LightCone8. This part of the tutorial is about potentially useful cosmological insights to be gained from…
Eigenvectors

What Are Eigenvectors and Eigenvalues in Math?

/
37 Comments
Two important concepts in Linear Algebra are eigenvectors and eigenvalues for a linear transformation that is represented by a square matrix. Besides…
lightcone7

LightCone8 Tutorial Part I

/
2 Comments
LightCone 8 is a versatile tabulating/charting cosmological calculator, useful for understanding the expansion history of the universe (and even some future…
partialfractions

Introduction to Partial Fractions Decomposition

/
3 Comments
Partial fractions decomposition is an algebraic technique that can be used to decompose (break down) a product of rational expressions into a sum…
ODE2

How to Solve Nonhomogeneous Linear ODEs using Annihilators

/
5 Comments
My previous Insights article, Solving Homogeneous Linear ODEs using Annihilators, discussed several examples of homogeneous differential equations, equations…
ODE1

Solving Homogeneous Linear ODEs using Annihilators

/
8 Comments
In this Insights article we'll look at a limited class of ordinary differential equations -- homogeneous linear ODES with constant coefficients. Although…
lineartransformations

Learn About Matrix Representations of Linear Transformations

/
19 Comments
Let X and Y be finite-dimensional vector spaces. Let ##T:X\to Y## be a linear transformation. Let ##A=(e_1,\dots,e_n)## and ##B=(f_1,\dots,f_m)## be ordered…
pythondebug2

Simple Python Debugging with Pdb: Part 2

/
2 Comments
This Insight article is the continuation of the first article, Simple Python Debugging with Pdb: Part 1.In this article, let's look at another important…
pythondebug1a

Learn Simple Python Debugging with Pdb

/
6 Comments
I'm pretty new to Python, so I was looking around for some debugging tools. At first, I dismissed Pdb (Python debugger) as being too primitive, but after…
cardinalnumbers

Informal Introduction to Cardinal Numbers

/
1 Comment
Cardinal numbers We will now give an informal introduction to cardinal numbers. We will later formalize this by using ordinal numbers. Informally, cardinal…
999

Is There a Rigorous Proof Of 1 = 0.999…?

/
102 Comments
Yes.First, we have not addressed what 0.999... means. So it's best first to describe what on earth the notation [tex]b_0.b_1b_2b_3...[/tex] means.…
blackholesforce

An Equation for the Centrifugal Force Reversal Near A Black Hole

/
15 Comments
My goal in this article is to derive a simple equation for the proper acceleration of an observer traveling on a circular path around a Schwarzschild black…
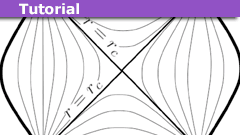
birktheo

Learn A Short Proof of Birkhoff’s Theorem

/
8 Comments
Birkhoff's theorem is a very useful result in General Relativity, and pretty much any textbook has a proof of it. The one I first read was in Misner, Thorne,…
heat errors

Frequently Made Errors in Heat: Elementary Level

/
3 Comments
1. Heat, Work, Internal Energy, and Kinetic Energy "If heat is the motion of molecules, why isn't it Kinetic Energy?"In everyday use, we may think…
Distributions

Errors in Probability: Continuous and Discrete Distributions

/
1 Comment
1. Classifying as discrete, continuous, or mixed These statements (or equivalents) can be found in authoritative-seeming websites:X "A random variable…
Coriolis

Frequently Made Errors: Pseudo and Resultant Forces

/
12 Comments
  1. Real versus Fictitious Pseudo, or "fictitious", forces can arise when a non-inertial frame of reference is used. Using a non-inertial frame…
renormalization2

Why Renormalisation in Quantum Theory Needs a Cutoff

/
31 Comments
Introduction This is a follow on from my paper explaining renormalization. A question was raised - why exactly do we need a cut-off. There is a deep reason…
errors springs

Frequently Made Errors in Mechanics: Springs

/
3 Comments
  1. Springs in Series "A spring of constant ##k_1## is connected in series with a spring of constant ##k_2##.  What is the spring constant…
natural language errors

Frequently Made Errors in Probability: Conditionals in Natural Language

/
2 Comments
  1. Turning a verbal condition into Algebra An actual thread..."A study of auto accidents has found that 40% of all fatal accidents are…
impact errors

Frequently Made Errors in Mechanics: Momentum and Impacts

/
1 Comment
  An impact is an impulse (change of momentum) that involves arbitrarily large forces acting very briefly. These result in near-instantaneous…
hydrostatics

Frequently Made Errors in Mechanics: Hydrostatics

/
3 Comments
  1. Archimedes' Principle X "When a body is placed in a liquid, the weight of the body equals the weight of the liquid displaced"That will…
variables

Some Conceptual Difficulties in the Roles of Variables and Constants

/
3 Comments
1. Variables and Constants When is a constant not a constant?  When it varies.In the standard equation ##y=ax+b##, we are used to thinking of x and…
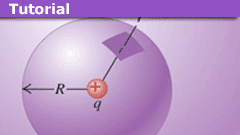
gausslaw

Learn a Partial “Derivation” of Gauss’s Law

/
3 Comments
Gauss's law was formulated by Carl Friedrich Gauss in 1835. It is one of the four Maxwell's equations that form the basis of classical electrodynamics.…
error handling

Frequently Made Errors in Equation Handling

/
15 Comments
  1. Algebra versus Arithmetic When numerical values are provided as inputs in a question, it is tempting to plug these into the equations…
kinematic errors

Frequently Made Errors in Mechanics: Kinematics

/
11 Comments
  Kinematics is the subset of dynamics that only concerns itself with time, displacement, velocity, and acceleration. A problem is…
mistakes moments

Frequently Made Errors in Mechanics: Moments

/
7 Comments
 The term "moment" is used in various ways in Physics and Mathematics:Given a force and a reference point, the force has a moment (or…
renormalization

Quantum Renormalisation Made Easy

/
24 Comments
What Is The Issue With Renormalisation If you have an interest in physics you have likely come across renormalisation before, although what it really…
electrical wire

Misconceiving Mutual Inductance Coefficients

/
4 Comments
 A commonly used formula for mutual inductance M between two nearby coils L1 and L2 is M = k√(L1*L2). This formula however assumes equal percentage…
friction

Frequently Made Errors in Mechanics: Friction

/
8 Comments
  1. Direction of the normal Definition: The normal force that body A exerts on body B is that force of minimum magnitude which suffices to…
differentiable function 2

A Continuous, Nowhere Differentiable Function: Part 2

/
2 Comments
This is Part 2 of a series of articles in which the goal is to exhibit a continuous function that is nowhere differentiable and to explore some interesting…
forces mistakes

Frequently Made Errors in Mechanics: Forces

/
35 Comments
 Notation: On this page, a circumflex signifies an average. 1. Forces as vectors A force is a vector, i.e. has magnitude and direction.…
2D Animation

How to Visualize the 2-D Particle in a Box

/
11 Comments
Introduction The particle in a box is a staple of entry-level Quantum Mechanics classes because it provides a meaningful contrast between classical and…
differentiable function

A Continuous, Nowhere Differentiable Function: Part 1

/
12 Comments
When studying calculus, we learn that every differentiable function is continuous, but a continuous function need not be differentiable at every point.…
Thermodynamics

Understanding Entropy and the 2nd Law of Thermodynamics

/
74 Comments
Introduction The second law of thermodynamics and the associated concept of entropy have been sources of confusion for thermodynamics students for centuries.…