Scientific Inference: Logical Induction Ain’t Logical

 

Three million years ago, the grandfathers of our genus used sharpened stones to chop wood and cut bone. Today, surgeons use fiber optic-guided lasers to clear micro blockages in the heart. Within our own lives, we’ve gone from burning our mouths on hot soup as children to cautiously blowing on the first spoonful as adults. These are examples of learning, of individuals and species adapting their behaviors and modifying their worlds in response to life experience. That we have learned is undeniable, but 300 years ago David Hume argued convincingly that this process of learning is not logically founded, and that no formal proof of its effectiveness exists. What then of humanity’s most prized system of inquiry, the scientific method? Most of us are convinced that astronomy gets closer to the true nature of things than astrology, but Hume’s argument not only blurs the distinction, it claims that no such comparison can be made. To the practicing scientist who is primarily concerned with collecting data, publishing papers, going to great locales for conferences, and so on, these are mere academic concerns to trouble only philosophers; after all, scientists are just driving the car, they don’t care about what’s buzzing under the hood. But Hume’s challenge is a deep stab at the heart of the scientific enterprise that flies in the face of basic experience, one that has resisted centuries of concerted effort at finding a resolution. Even if we don’t care about the formalities, in exploring this problem we’ll come to better understand the practice of science and how we come to know stuff.

Part 1. “Logical induction ain’t logical” – David Hume

Most of us are familiar with logical arguments like:

1. All priests are men.
2. Father Jim is a priest.
_____________________
therefore Father Jim is a man.

This is an example of a logical deduction: the truth of the conclusion is guaranteed by the truth of the premises so long as we follow the rules of deductive logic. The thing about deduction is that the conclusions never tell us anything new, since they are always fully entailed, if only implicitly, by the premises. In the example above, the fact that Father Jim is a man is already contained within the two premises—the conclusion merely makes the statement explicit. Because deductions never tell us anything new, they cannot increase, or amplify, our knowledge—they are said to be non-ampliative. How is it that we know the premises are true? Because, among other things, being a man is a requirement for being a priest—this deduction is true by definition.

What about this:

The sun has risen on Earth
every day for the past 4.5 billion years.
_________________________
therefore the sun will rise tomorrow.

Here the premise is true—it is based on historical knowledge—but the conclusion, which refers to the future, does not follow. Regardless of how certain we feel, the conclusion is not guaranteed because it contains information not provided on the premises. This kind of inference, in which the premises do not necessarily entail the conclusion, is called induction. You can think of it as the less-certain cousin of deduction. The above conclusion is tantamount to saying that the Sun will rise every day because there’s nothing in the premises that singles out “today” as particularly special. This is the essence of induction: from the observation of individual particular cases, we project universal generalizations. In the case of the rising sun, we have many, many individual observations and so we might suspect, though maybe not logically guaranteed, that our future projection is solid.

But what about this:

5 jellybeans, all of which have been black,
have been selected from a jar containing 100 jellybeans.
________________________________
therefore all jellybeans in the jar are black.

We feel less sure of this conclusion because there seem to be too few observed cases to speculate with much confidence about the larger collection of jellybeans. Inductive reasoning spans the spectrum of inference: from deduction (truth by logical necessity) to the tenuous assertion, to the most egregious non-sequiturs (see Figure 1). Ideally, our inferences should be inductively strong, as close to the deductive end of the scale as possible.

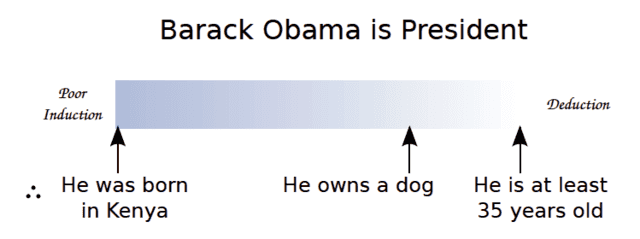
Fig 1. The sliding scale of induction, from poor inductive reasoning to the deduction.

Strong inductive arguments are ones in which the conclusions follow from the premises with high probability, like the case of the rising sun. Sometimes the conclusion forms the basis of a hypothesis—a more general statement or principle that includes the premises as particular cases. This generality is achieved through inductive reasoning by extrapolating particular observations across time, space, or jellybeans in jars. The problem is that we have no way of knowing how reliable it is.

Consider the following:

Induction has worked reasonably well in the past
________________________________________
therefore induction will work reasonably well in the future.

This is an inductive argument concerning induction itself. Assuming the premise is true, we expect the conclusion, that induction will continue to work reasonably well in the future, to be true. Seem circular? It is, badly so. This is the problem of induction. Hume nailed it in 1748 [1]

“…there can be no demonstrative arguments to prove, that those instances, of which we have no experience, resemble those, of which we have had experience…even after the observation of the frequent or constant conjunction of objects, we have no reason to draw any inference concerning any object beyond those of which we have had experience.”

Hume’s challenge is that the success of induction, arguably the method of establishing natural law since the Enlightenment, cannot be formally demonstrated. Philosopher Willard V. Quine offers a 20th-century view: “The brute irrationality of our sense of similarity, its irrelevance to anything in logic and mathematics, offers little reason to expect that this sense is somehow in tune with the world…Why induction should be trusted, apart from special cases such as the ostensive learning of words, is the perennial philosophical problem of induction.” [5]

The solution is at least intuitively obvious: there must be some fundamental uniformity within nature on which to anchor our extrapolations. But there are so many ways that nature might appear uniform: so many true regularities, so many perceived but unrelated correlations, so many random occurrences. Unless the requisite uniformity exists a priori (a likely untenable proposition, regardless of what Herr Kant might think), it must be established empirically—a feat that necessarily involves induction, taking us right back to the start. There have been many contemporary attempts to solve Hume’s problem (see, for example, [2] and [3]), but all are inextricably self-referential and question-begging; all ultimately fail. This is not surprising, because there can be no resolution to the problem in general. How do we know whether an inductive argument is likely correct? We don’t—we can’t—because the conclusion is not based on experience nor a logical consequence of it. Following philosopher Nelson Goodman we adopt the view that Hume’s problem is “not a problem of demonstration, but a problem of defining the difference between valid and invalid predictions” [4] (emphasis mine), that is, the method of induction must be taken as given: the challenge is the more practical one of knowing when we can and cannot apply it.

To illustrate this point, say a die is rolled one million times with each face coming up very nearly 1/6 of the time. We are pretty confident that the die is fair, and if asked to bet on whether the next two rolls will be sixes, we’d bet odds 36-to-1 against. And if the existence of the gambling industry is any proof, we’d be substantiated in this judgment. The roll of the die is a relatively simple phenomenon with readily recognizable symmetry—we can apply induction with high confidence. Meanwhile, Hume’s concern seems quite immaterial, amounting to the warning that the universe might one day change, abruptly, in such a way that those odds shift, that the die roll no longer conforms to the same long-running averages. This is impossible to guard against—the problem of induction is not about our troubles in dealing with a potentially arbitrary and capricious universe. The problem is instead one of how to isolate the regularities relevant to the system under investigation in the face of incomplete knowledge. We cannot prescribe rules for how to do this in general (echoing Goodman, the problem is not one of demonstration), but the validity of individual hypotheses about the world can be decided from within the system of inductive inference.

Because the uniformity emerges clearly after many trials, the Roll of the Die is a simple and notable success story. Not all problems are this easy. Suppose we are looking for a mathematical expression governing a certain physical process. As data, we have the numbers $1, 3, 5, 7, 9, \cdots$. The sequence is generated by the expression $x_n = 2n+1$, starting from $n=0$, and our prediction for the $6^{\rm th}$ number is $x_5 = 11$. Meanwhile, a rival team of researchers advances the prediction $x_5 = 3845$, based on the relation
\begin{equation}
x_n = (1 – 2n-1)(3 – 2n-1)(5-2n-1)(7-2n-1)(9-2n-1)+2n+1.
\end{equation}
Both sequences describe the regularity of the data equally well, but they make wildly different extrapolations beyond them. We can think of the alternative sequences as two competing hypotheses, and the challenge is to select the one that best generalizes the given data.

Nelson Goodman found an insightful way of articulating this problem. All emeralds that have ever been observed have been green. Suppose there is some other disposition of color called “grue”, such that something that is grue is green before, say, July 1, 2100, and blue afterward. All emeralds that have ever been observed have also then been grue. Now, which color do we predict for yet-to-be-observed emeralds? If we project green we will be correct, whereas a projection of grue will throw us a curveball—it will not support a strong inductive inference once the calendar ticks past July 1, 2100. This example is deliberately artificial, but Goodman’s point is an important one: there is no clear way to differentiate projectable properties, like green, from non-projectable ones, like grue. Goodman suggests experience as a guide: “Plainly, ‘green’, as a veteran of earlier and many more projections than ‘grue’, has the more impressive biography. The predicate ‘green’, we may say, is much better entrenched than the predicate “grue” [4]. So while there is no hard rule for distinguishing projectable from non-projectable characteristics, we expect that our acquaintance with the world should inspire our ability to tease out the essential characteristics of the system under study. Not foolproof though, and not always helpful: for example, experience doesn’t suggest which expression for $x_n$ above is projectable. The problem of projectability is pervasive and formidable: Goodman named it the “new riddle of induction”.

The struggle against Hume’s problem of induction has moved from the philosophical high ground to the front lines of applied science. We have passed on solving the meta-problem of induction as a method, focusing instead on our ability to discern projectable patterns in the data logbook in support of strong inductive inference. In science, we are given an incomplete glimpse of a small part of the world, and it’s easy to suppose that induction, however imperfect, is the only way to complete the picture, but this view is not without its challenges. Let’s put induction on hold for a while, and investigate some other approaches to the problem of scientific inference.

Continue to: Part 2. “We don’t need no stinkin’ induction” – Sir Karl Popper

References

[1] An Enquiry Concerning Human Understanding, David Hume (1748).
[2] Choice & Chance: An Introduction to Inductive Logic, Brian Skyrms, Dickenson Pub. Co. (1986).
[3] The Foundations of Scientific Inference, Wesley Salmon, Univ. of Pittsburgh Press (1979).
[4] Fact, Fiction, and Forecast, Nelson Goodman, Harvard University Press (1954)
[5] Natural Kinds, W. V. Quine, in Ontological Relativity & Other Essays, Columbia University Press (1969)