SOHCAHTOA: Seemingly Simple, Conceivably Complex

What is SOHCAHTOA

SOHCAHTOA is a mnemonic acronym used in trigonometry to remember the relationships between the sides and angles of right triangles. Each letter in “SOHCAHTOA” stands for a specific trigonometric function:

1. Sine (sin): The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite that angle to the length of the hypotenuse (the longest side). Mathematically, sin(θ) = opposite/hypotenuse.
2. Cosine (cos): The cosine of an angle is defined as the ratio of the length of the adjacent side (the side next to the angle but not the hypotenuse) to the length of the hypotenuse. Mathematically, cos(θ) = adjacent/hypotenuse.
3. Tangent (tan): The tangent of an angle is defined as the ratio of the length of the side opposite that angle to the length of the adjacent side. Mathematically, tan(θ) = opposite/adjacent.

SOHCAHTOA is a helpful tool for students and learners to quickly recall these trigonometric relationships when working with right triangles and solving trigonometric problems. It simplifies the process of finding unknown side lengths or angles in right triangles using trigonometric functions.

Preface

My first experience with derivatives was seeing how they are obtained from the usual definition
$$f'(x)=\underset{\text{$\Delta $x}\to 0}{\text{Lim}}\frac{f (\text{$x+\Delta $x})-f (x)}{\text{$\Delta $x}}.$$

I accepted the binomial theorem derivation in the case of polynomials and the small-angle explanation in the case of sines and cosines until my math instructor asserted, without justification, that the derivative of the exponential is itself. I had to wait until Taylor expansions to understand the exponential derivative. At that time I also saw the series for the cosine and sine, which up to that point I knew as the ratio of one or the other right side to the hypotenuse in a right triangle. I reached graduate school having stored the trigonometric functions, the unit circle, the right triangle side ratios, and the series expansions in appropriate compartments in my brain, ready to use them correctly but not bothering to understand how and if they were connected.

I first encountered SOHCAHTOA in graduate school as a TA when I saw it scribbled on a student’s test. I had to ask a more experienced TA what it meant and whether it merited partial credit as “work shown”.  (The reader who is not familiar with the acronym, or has mercifully forgotten it, may find this  Soh Cah Toa Song informative if not mildly entertaining.)  Not too long later, I heard the passing remark that the solution to the differential equation for the simple harmonic oscillator can be thought of as the definition for the sine and cosine, much like Legendre polynomials, Bessel functions, etc. are defined by the equations to which they are solutions. Although the remark provided me with a fresh point of view, it added to my befuddlement. If sines and cosines are (a) defined as solutions of a differential equation and (b) expressed as infinite series, where and how does their geometric definition enter the picture? Handheld calculators add series to display numerical values for sines and cosines; they do not take ratios of sides of right triangles. Whence SOHCAHTOA?

I wrote this insight intending to present how I was eventually able to reconcile these ideas in my mind.  I attempted to proceed along a top-down, “smoothed over” sequence and tried not to beg any questions.  Little did I know that the final reconciliation would occur after I finished writing and started thinking about the final Afterthoughts section. This narrative is intended for those who, like me, came away from a calculus course with a fuzzy notion of how things fit together.

The Exponential

We begin with a function f(x) which is its first derivative. As an infinite series, this function is
$$f(x)=\frac{1^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+\text{…}=\sum _{n=0}^{\infty } \frac{x^n}{n!},$$an identification that is verifiable by direct differentiation.

This function can be written as $f(x) = e^x$, where e is an appropriate constant base.

Proof
Start with the derivative of the product $f(x)f(\text{-}x)$,$$\frac{d}{dx}[f(x)f(\text{-}x)]=f(x)\frac{df(\text{-}x)}{dx}+f(\text{-}x)\frac{df(x)}{dx}$$For the derivative in the first term, define $\xi \equiv \text{-}x.$ Then,$$\frac{df(\text{-}x)}{dx}=\frac{df(\xi)}{dx}=\frac{df(\xi)}{d\xi}\frac{d\xi}{dx}=f(\xi)(\text{-}1)=\text{-}f(\text{-}x).$$For the derivative in the second term, by definition $\dfrac{d}{dx}f(x)=f(x)$.
Thus,$$\frac{d}{dx}[f(x)f(\text{-}x)]=f(x)[\text{-}f(\text{-}x)]+f(\text{-}x)f(x)=0.$$This means that the product $f(x) f(\text{-}x)$ is constant for all values of $x$. Specifically, when $x = 0$, $f (0) f (0) = 1.$  Hence $f(x)f(\text{-}x)=1$.  Thus, $f(\text{-}x)$ is the inverse of $f(x)$ which means we can write $f(x)=e^x$ where $e$ is an appropriate constant base, Q.E.D.

The numerical value of the base $e$ is obtained by evaluating $f(1)$,$$e=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\text{…}=\sum _{n=0}^{\infty } \frac{1}{n!}.$$

Sines and Cosines

Consider the case when the argument of the exponential is purely imaginary, $x = i \theta$. (At this point $\theta$ is just a real parameter; its identification as an angle will come later.) Then
$$e^{i \theta }=1+\frac{\text{i$\theta $}}{1!}-\frac{\theta ^2}{2!}-\frac{\text{i$\theta $}^3}{3!}+\text{…}$$The real and imaginary parts of $\theta$ can be regarded as two separate functions, which we name $\cos(\theta)$ and $\sin(\theta)$. Then$$\cos(\theta) \equiv \rm{Re}\left(e^{i \theta }\right)=1-\frac{\theta ^2}{2!}+\frac{\theta ^4}{4!}-\text{…}~~~~~(1 a)$$
$$\sin(\theta) \equiv \rm{Im}\left(e^{i \theta }\right)=\frac{\theta^1}{1!}-\frac{\theta ^3}{3!}+\frac{\theta ^5}{5!}-\text{…}~~~~~(1 b)$$and, of course,$$e^{i\theta}=\cos(\theta)+i\cos(\theta)~~~~~(1 c)$$It follows from definitions (1a) and (1b) that$$\frac{d}{d\theta}\cos(\theta)=-\sin(\theta)~;~~\frac{d}{d\theta}\sin(\theta)=\cos(\theta)~~~~~(1 d)$$

Now consider the more general case when the argument of the exponential is an arbitrary complex number, $x = a + i b$ where $a$ and $b$ are real. Then $e^ix$ is a complex number $z$,$$z=e^{{ix}}= e^{i (a+{ib})}=e^{-b} e^{{ia}}$$

The modulus squared is

$$\left|z|^2\right.=z z^*=e^{-b} e^{-b} e^{\text{ia}} e^{-\text{ia}}=e^{-2 b}$$

It follows that, with renaming $\rho= e^{-b}$ and $a = \theta$, we can write any complex number in the form$$z=\rho e^{i \theta}$$ in which case $$\left|z|^2\right.=(\rho e^{i \theta }) (\rho e^{-i \theta })=\rho ^2~~~~~(2 a)$$But also$$z=\rho e^{i \theta }=\rho [\cos((\theta ) +i \sin(\theta)]$$in which case$$\left|z|^2\right.=\rho e^{i \theta }\rho e^{-i \theta }=\rho [\cos((\theta ) +i \sin(\theta)]\rho [\cos((\theta ) -i \sin(\theta)]=\rho^2[\cos^2(\theta)+sin^2(\theta)]~~~~~(2 b)$$

By combining Eq. (2a) and (2b),$$\cos^2(\theta)+sin^2(\theta)=1 ~~~~~(3)$$The complex number $z$ can also be written in terms of its real imaginary parts as $=u+iv$, so that$$\left|z|^2\right.=z z^*=(u+i v) (u-i v)=u^2+v^2$$

It follows from the above equations that

$$\rm{Re}(z)=\rho \cos(\theta)~~~~~(4)$$ $$\rm{Im}(z)=\rho \sin(\theta)~~~~~(5)$$ $$u^2+v^2=\rho^2~~~~~(6)$$Furthermore, from the series definitions of the cosine and the sine, $\cos(0)=1;~\sin(0)=0.$

The Pythagorean Theorem

Complex number $z$ can be represented in the u-v plane as an ordered pair {u,v}. Equations (4) and (5) indicate that a parametric curve with $\theta$ as the parameter can be generated in the u-v plane at constant $\rho$. We will show that this curve is a circle of radius $\rho$ centered at the origin.

The figure below illustrates a segment of the parametric curve at constant $\rho$. Consider point ${u_1,v_1}$ on the curve representing complex number $z_1$ at $\theta=\theta_1$. Draw a radial line of length $r$ from the origin to the point. The slope (rise over run) of the radial line is
$m=\dfrac{v_1}{u_1}.$
From equations (4) and (5), $m=\dfrac{v_1}{u_1}=\dfrac{\sin(\theta_1)}{\cos(\theta_1)}.$

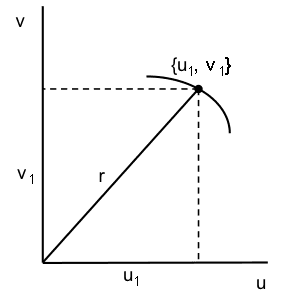
The slope (not shown) of the parametric curve at the same point is

$m’=\left. \dfrac {dv}{du} \right|_{u=u_1}.$

Using equations (4) and (5) we take derivatives at constant $\rho$.$$m’=\left.\frac{\partial v}{\partial \theta }\frac{\partial \theta }{\partial u}\right|_{\theta=\theta_1}=\rho \cos(\theta_1) \left[ \frac{-1}{\rho \sin(\theta_1)} \right]=-\frac{1}{\frac{ \sin(\theta_1) }{ \cos(\theta_1) }}$$

It follows that the product of the slopes is $m\times m’=\text{-}1$ indicating that they are perpendicular.  Since the chosen point is arbitrary, the two slopes are perpendicular for any value of parameter $\theta$. This means that as $\theta$ varies, the point of intersection traces a circle in the u-v plane. Therefore the radial segment $r$ from the origin to a point on the parametric curve is a radius of this circle.

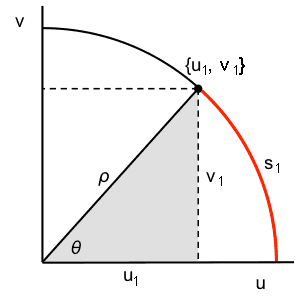
At $\theta = 0$, $z(0) =\rho e^{i*0}= \rho$ and $z(0) = \{u(0) ,v(0)\} = \{\rho, 0\}.$ But this point is also on the parametric circle of radius $r$, therefore we identify the radius of the circle $r$ as being equal to $\rho$, the modulus of $z$.  Thus, for the triangle shown in the figure above, $u_1^2+v_1^2=r^2=\rho^2$.

This relation holds for all values of parameter $\theta$ and radius $r$ which in turn makes it true for all right triangles and “proves” the Pythagorean theorem. (See the Afterthoughts section below for the explanation of the quotation marks.)

Parameter $\theta$ as the polar angle

We will now show that parameter $\theta$ is the angle between the radial vector and the real axis $u$.

Using the Pythagorean theorem, we consider a displacement by an element of arc $ds$ along the circle. The corresponding elements $du$ and $dv$ along the real and imaginary axes are perpendicular to each other. In the limit $ds\rightarrow 0~$they are related by the Pythagorean theorem,$$ds=\sqrt{(du)^2+(dv)^2}=\sqrt{(du)^2}\sqrt{1+\left( dv/du\right)^2}$$Remembering equations (1d) and (4) $$du=-\rho \sin(\theta)d\theta~\rightarrow~\sqrt{(du)^2}=\rho \sin(\theta)d\theta$$and$$\sqrt{1+\left(\frac{ dv}{du}\right)^2}=\sqrt{1+\left[\frac{ \cos(\theta)}{\sin(\theta)}\right]^2}=\frac{1}{\sin(\theta)}$$so that$$ds=\rho \sin(\theta)d\theta \times \frac{1}{\sin(\theta)}=\rho d\theta$$

If we now move along the circle starting at the real axis to point $\{u_1,v_1\}$ located at value $\theta = \theta_1$, the arc on the circle has length$$s_1=\int_0^{\theta_1}\rho d\theta=\rho \ \theta_1~\rightarrow \theta_1=\frac{s_1}{\rho}.$$This identifies parameter $\theta$ as the angle formed by the radius and the real axis $u$. We conclude that the real and imaginary part of the complex exponential $e^{i \theta}$ can be represented geometrically as the ratios of the right sides to the hypotenuse of a right triangle having an acute angle $\theta.$ Remembering equations (4) and (5), we obtain the familiar relations

$$\sin(\theta)=\frac{v}{\rho}=\frac{\rm{opposite}}{\rm{hypotenuse}}~~~~(\rm{SOH})$$

$$\cos(\theta)=\frac{u}{\rho}=\frac{\rm{adjacent}}{\rm{hypotenuse}}~~~~(\rm{CAH})$$

The auxiliary definition

$$\tan(\theta)=\frac{v}{u}=\frac{\rm{opposite}}{\rm{adjacent}}~~~~(\rm{TOA})$$

is the slope of the radial line and

$$\cot(\theta)=\frac{u}{v}=\frac{\rm{adjacent}}{\rm{opposite}}$$is the negative of the tangent to the circle at angle $\theta.$

Afterthoughts

After committing to draft my thoughts up to this point, I delayed posting for four months, wondering whether I have presented an algebraic proof of the Pythagorean theorem among the rest of the stuff.  Probably not. With a good drawing based on the unit circle (hyp = 1), it is not difficult to show geometrically that $$\Delta(\mathrm{opp})=(\mathrm{adj})\Delta \theta;~\Delta(\mathrm{adj})=-(\mathrm{opp})\Delta \theta$$from which it follows that$$\frac{\Delta}{\Delta \theta}\left[\frac{\Delta(\mathrm{opp})}{\Delta \theta}\right]=-(\mathrm{opp});~\frac{\Delta}{\Delta \theta}\left[\frac{\Delta(\mathrm{adj})}{\Delta \theta}\right]=-(\mathrm{adj}).$$It seems then that there are two parallel formulations, one algebraic and one geometric, that exist independently and are linked by the isomorphism between the complex and Euclidean planes.  I don’t think that what I initially set out to achieve, namely derive SOH CAH TOA algebraically, can be done. Nevertheless, as I wrote this insight and thought about all this,  I dispelled once and for all the fuzziness in how all these ideas fit together.

Comments Thread