Struggles With The Continuum: Quantum Mechanics of Charged Particles
Last time we saw that nobody yet knows if Newtonian gravity, applied to point particles, truly succeeds in predicting the future. To be precise: for four or more particles, nobody has proved that almost all initial conditions give a well-defined solution for all times!
The problem is related to the continuum nature of space: as particles get arbitrarily close to each other, an infinite amount of potential energy can be converted to kinetic energy in a finite amount of time.
I left off by asking if this problem is solved by more sophisticated theories. For example, does the ‘speed limit’ imposed by special relativity help the situation? Or might quantum mechanics help, since it describes particles as ‘probability clouds’, and puts limits on how accurately we can simultaneously know both their position and momentum?
We begin with quantum mechanics, which indeed does help.
Table of Contents
The quantum mechanics of charged particles
Few people spend much time thinking about ‘quantum celestial mechanics’—that is, quantum particles obeying Schrödinger’s equation, that attract each other gravitationally, obeying an inverse-square force law. But Newtonian gravity is a lot like the electrostatic force between charged particles. The main difference is a minus sign, which makes like masses attract, while like charges repel. In chemistry, people spend a lot of time thinking about charged particles obeying Schrödinger’s equation, attracting or repelling each other electrostatically. This approximation neglects magnetic fields, spin, and indeed anything related to the finiteness of the speed of light, but it’s good enough to explain quite a bit about atoms and molecules.
In this approximation, a collection of charged particles is described by a wavefunction ##\psi##, which is a complex-valued function of all the particles’ positions and also of time. The basic idea is that ##\psi## obeys Schrödinger’s equation
$$ \frac{d \psi}{dt} = – i H \psi $$
where ##H## is an operator called the Hamiltonian, and I’m working in units where ##\hbar = 1##.
Does this equation succeed in predicting ##\psi## at a later time given ##\psi## at time zero? To answer this, we must first decide what kind of function ##\psi## should be, what concept of derivative applies to such functions, and so on. These issues were worked out by von Neumann and others starting in the late 1920s. It required a lot of new mathematics. Skimming the surface, we can say this.
At any time, we want ##\psi## to lie in the Hilbert space consisting of square-integrable functions of all the particle’s positions. We can then formally solve Schrödinger’s equation as
$$ \psi(t) = \exp(-i t H) \psi(0) $$
where ##\psi(t)## is the solution at time ##t##. But for this to really work, we need ##H## to be a self-adjoint operator on the chosen Hilbert space. The correct definition of ‘self-adjoint’ is a bit subtler than what most physicists learn in the first course on quantum mechanics. In particular, an operator can be superficially self-adjoint—the actual term for this is ‘symmetric’—but not truly self-adjoint.
In 1951, based on the earlier work of Rellich, Kato proved that ##H## is indeed self-adjoint for a collection of nonrelativistic quantum particles interacting via inverse-square forces. So, this simple model of chemistry works fine. We can also conclude that ‘celestial quantum mechanics’ would dodge the nasty problems that we saw in Newtonian gravity.
The reason, simply put, is the uncertainty principle.
In the classical case, bad things happen because the energy is not bounded below. A pair of classical particles attracting each other with an inverse square force law can have arbitrarily large negative energy, simply by being very close to each other. Since energy is conserved, if you have a way to make some particles get an arbitrarily large negative energy, you can balance the books by letting others get an arbitrarily large positive energy and shoot to infinity in a finite amount of time!
When we switch to quantum mechanics, the energy of any collection of particles becomes bounded below. The reason is that to make the potential energy of two particles large and negative, they must be very close. Thus, their difference in position must be very small. In particular, this difference must be accurately known! Thus, by the uncertainty principle, their difference in momentum must be very poorly known: at least one of its components must have a large standard deviation. This in turn means that the expected value of the kinetic energy must be large.
This must all be made quantitative, to prove that as particles get close, the uncertainty principle provides enough positive kinetic energy to counterbalance the negative potential energy. The Kato–Lax–Milgram–Nelson theorem, a refinement of the original Kato–Rellich theorem, is the key to understanding this issue. The Hamiltonian ##H## for a collection of particles interacting by inverse square forces can be written as
$$ H = K + V $$
where ##K## is an operator for the kinetic energy and ##V## is an operator for the potential energy. With some clever work one can prove that for any ##\epsilon > 0##, there exists ##c > 0## such that if ##\psi## is a smooth normalized wavefunction that vanishes at infinity and at points where particles collide, then
$$ | \langle \psi , V \psi \rangle | \le \epsilon \langle \psi, K\psi \rangle + c. $$
Remember that ##\langle \psi , V \psi \rangle## is the expected value of the potential energy, while ##\langle \psi, K \psi \rangle## is the expected value of the kinetic energy. Thus, this inequality is a precise way of saying how kinetic energy triumphs over potential energy.
By taking ##\epsilon = 1##, it follows that the Hamiltonian is bounded below on such
states ##\psi##:
$$ \langle \psi , H \psi \rangle \ge -c . $$
But the fact that the inequality holds even for smaller values of ##\epsilon## is the key to showing ##H## is ‘essentially self-adjoint’. This means that while ##H## is not self-adjoint when defined only on smooth wavefunctions that vanish at infinity and at points where particles collide, it has a unique self-adjoint extension to some larger domain. Thus, we can unambiguously take this extension to be the true Hamiltonian for this problem.
To understand what a great triumph this is, one needs to see what could have gone wrong! Suppose space had an extra dimension. In 3-dimensional space, Newtonian gravity obeys an inverse square force law because the area of a sphere is proportional to its radius squared. In 4-dimensional space, the force obeys an inverse cube law:
$$ F = -\frac{Gm_1 m_2}{r^3} . $$
Using a cube instead of a square here makes the force stronger at short distances, with dramatic effects. For example, even for the classical 2-body problem, the equations of motion no longer ‘almost always’ have a well-defined solution for all times. For an open set of initial conditions, the particles spiral into each other in a finite amount of time!
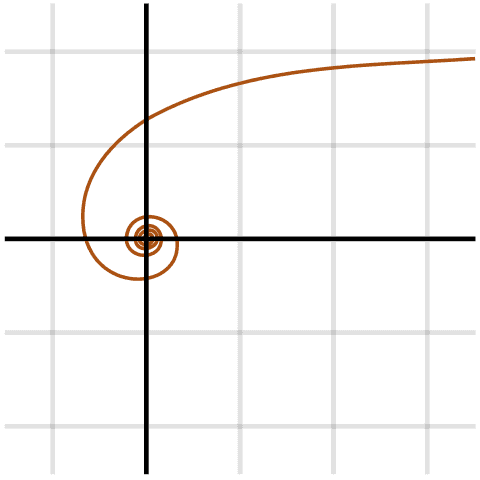
Hyperbolic spiral – a fairly common orbit in an inverse cube force.
The quantum version of this theory is also problematic. The uncertainty principle is not enough to save the day. The inequalities above no longer hold: kinetic energy does not triumph over potential energy. The Hamiltonian is no longer essentially self-adjoint on the set of wavefunctions that I described.
In fact, this Hamiltonian has infinitely many self-adjoint extensions! Each one describes different physics: namely, a different choice of what happens when particles collide. Moreover, when ##G## exceeds a certain critical value, the energy is no longer bounded below.
The same problems afflict quantum particles interacting by the electrostatic force in 4d space, as long as some of the particles have opposite charges. So, chemistry would be quite problematic in a world with four dimensions of space.
With more dimensions of space, the situation becomes even worse. In fact, this is part of a general pattern in mathematical physics: our struggles with the continuum tend to become worse in higher dimensions. String theory and M-theory may provide exceptions.
Next time we’ll look at what happens to point particles interacting electromagnetically when we take special relativity into account. After that, we’ll try to put special relativity and quantum mechanics together!
For more
For more on the inverse cube force law, see:
• John Baez, The inverse cube force law, Azimuth, 30 August 2015.
It turns out Newton made some fascinating discoveries about this law in his Principia; it has remarkable properties both classically and in quantum mechanics.
The hyperbolic spiral is one of 3 kinds of orbits possible in an inverse cube force; for the others see:
• Cotes’s spiral, Wikipedia.
The picture of a hyperbolic spiral was drawn by Anarkman and Pbroks13 and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license.
I’m a mathematical physicist. I work at the math department at U. C. Riverside in California, and also at the Centre for Quantum Technologies in Singapore. I used to do quantum gravity and n-categories, but now I mainly work on network theory and the Azimuth Project, which is a way for scientists, engineers and mathematicians to do something about the global ecological crisis.






Sure, perhaps one should say that it gives a limit on a mass of the gravitational field. It’s analogous to the measurement of a “photon mass” in the context of electromagnetics. You can test this also by, e.g., high-accuracy measurements of Coulomb’s law, i.e., with classical em. field situations.
“But if we take GR to be a low energy effective quantum field theory of a spin 2 particle, then in that sense, wouldn’t LIGO say something about gravitons in the same way it says something about GR?”
Okay, if you insist. What I meant is that we don’t know anything more about quantum gravity than we did before LIGO discovered gravitational waves. This was a classical experiment, not a quantum one.
” At least it gives an upper limit of the graviton mass.”
Okay. If someone thought the graviton had a nonzero mass they might be less convinced of that now. Of course we already knew that either the graviton mass is zero or general relativity is wrong.
I would prefer to say LIGO’s first result can help us test a prediction of purely classical general relativity: namely, that gravitational waves don’t disperse, at least if they’re not too strong and their wavelengths are much shorter than the curvature length scale of the spacetime they’re in. You can interpret this in terms of gravitons if you like. But we’re no more (or less) sure that gravitons exist now than we were a few weeks ago.
At least it gives an upper limit of the graviton mass.
“The LIGO experiment is very important, but it says nothing at all about quantum gravity, gravitons or string theory. I explained why in the discussion thread here:
[LIST]
[*]John Baez, [URL=’https://plus.google.com/117663015413546257905/posts/EDCtyk28Ft1′]Gravitational waves[/URL], 11 February 2016.
[/LIST]
If you go there you’ll see a long conversation with at least 113 comments. I must have answered at least 40 interesting questions about LIGO and gravitational waves. It was quite fun!”
But if we take GR to be a low energy effective quantum field theory of a spin 2 particle, then in that sense, wouldn’t LIGO say something about gravitons in the same way it says something about GR?
The LIGO experiment is very important, but it says nothing at all about quantum gravity, gravitons or string theory. I explained why in the discussion thread here:
[LIST]
[*]John Baez, [URL=’https://plus.google.com/117663015413546257905/posts/EDCtyk28Ft1′]Gravitational waves[/URL], 11 February 2016.
[/LIST]
If you go there you’ll see a long conversation with at least 113 comments. I must have answered at least 40 interesting questions about LIGO and gravitational waves. It was quite fun!
Hi John. About the LIGO experiment, do you think that there are new perspectives now on the exploration of the nature of space-time? what could be the implications of this measurements of gravitational waves? what about quantum gravity and gravitons? what about string theory? I’ve heard the announcement by the LIGO team, and they’ve talked about some cosmological strings. I don’t know if this place is the appropriate to talk about this, but this discovery excites me a lot! do you think that with this interferometers we will confirm or discard string theory?
Thanks for your interesting posts.
“Is this image even approximately a correct view of the theory?”
Yes, that’s a quite good description of what loop quantum gravity is aiming for. The main problem is that there are several different versions of loop quantum gravity and spin foam theories, nobody has been able to show (in any style I find convincing – I’m not hoping for mathematical rigor) that any version reduces to general relativity in a suitable ‘classical limit’.
“Is the problem with your Newtonian example due to the implied instantaneous-action-at-a-distance in the fundamental equation (which means the result isn’t fully conservative)?”
I don’t know what you mean by “not fully conservative”: energy is conserved in this theory, along with everything else that should be conserved.
I said what causes the problem I discussed (namely runaway solutions where particles shoot to infinity in finite time):
“Is this is a weakness in the theory, or just the way things go? Clearly it has something to do with three idealizations:
[LIST]
[*]point particles whose distance can be arbitrarily small,
[*]potential energies that can be arbitrariy large and negative,
[*]velocities that can be arbitrarily large.
[/LIST]
These are connected: as the distance between point particles approaches zero, their potential energy approaches −∞, and conservation of energy dictates that some velocities approach +∞.
”
The interesting thing is that when we introduce special relativity and make charged point particles interact via fields, the runaway solutions don’t go away. If anything, they get even worse! They don’t reach arbitrarily high speeds, but particles that should be attracting tend to shoot away from each other in an ever-accelerating way, approaching the speed of light. I explain this in [URL=’https://www.physicsforums.com/insights/struggles-continuum-part-3/’]Part 3[/URL].
Of course that’s for electromagnetism; I’ll talk about general relativity later.
“One final note. Your reply to the God-made/Man-made joke was uncomfortable but you have to remember that discussing the continuum is really the physics equivalent to a “religious” question.”
I try to avoid “religious” questions: this series of posts is about concrete problems with our favorite theories of physics. Here by “concrete problems” I mean things like runaway solutions and the actual behavior of electrons, which we can study using math and experiment – as opposed to questions like whether the real numbers “really exist” or were “made by Man”.
“It seems like the only thing we can do is perpetually oscillate between experimental and theoretical advances, never reaching a “ta da, we’re done!” moment.”
There’s so much we don’t understand yet about physics, I don’t think it’s even profitable to think about the “ta da, we’re done!’ moment. I think we’re making good progress, but it may take a few more millennia to understand the fundamental laws of physics. So, I think it’s good to be patient and enjoy the process of slowly figuring things out. It is, after all, plenty of fun.
Hi!
“But as far as you know, are there any promising attempts at developing a theory that is fundamentally discrete, at the most basic level? (So that continuum calculations are the approximations to the discrete calculations, rather than the other way around.) Does loop quantum gravity count as one?”
Count as fundamentally discrete, or count as promising? :smile:
Loop quantum gravity uses real numbers and infinite-dimensional Hilbert spaces all over – in fact, the approach favored by Ashtekar uses Hilbert spaces of uncountable dimension, which are much bigger than the usual infinite-dimensional Hilbert spaces in physics. It also continues to treat space as a continuum.
On the other hand, most versions of loop quantum gravity involve discretization of geometry in the sense that areas and volumes take on a discrete spectrum of allowed values, sort of like energies for the bound states of a hydrogen atom.
In spin foam models, which are a bit different than loop quantum gravity, we tried to remove the concept of a spacetime continuum, and treat it as a quantum superposition of different discrete geometries. However, the real and complex numbers were still deeply involved.
If I considered this line of work highly promising I would still be working on it. I would like to hope it’s on roughly the right track, but there’s really no solid evidence for that, and at some point that made me decide to quit and work on something that would bear fruit during my own lifetime. I think that was a wise decision.
“In fact all the most famous laws of physics are given as differential equations or path integrals over infinite-dimensional spaces of fields. These laws are models of reality. We can extract information from these models either by numerical methods, analytical methods, or a combination of the two.
For example, in [URL=’https://plus.google.com/117663015413546257905/posts/QsRKWT2VFDt’]computing the neutron/proton mass ratio[/URL] one starts with quantum chromodynamics and then applies a whole battery of analytical methods before doing Monte Carlo integration over fields defined on a discrete lattice, a kind of spacetime grid. Discrete difference equations don’t come into this at all. But my main point is this: nobody working in this subject thinks the lattice actually is spacetime: in fact, the analytical methods are used precisely to understand and correct for the errors introduced by discretization. Without these corrections the computation would be way off.”
Hi, John! It’s been a long time since sci.physics.research.
So, discrete methods (such as lattice calculations) are used as a calculational tool to get numbers out of a theory that is continuous. But as far as you know, are there any promising attempts at developing a theory that is fundamentally discrete, at the most basic level? (So that continuum calculations are the approximations to the discrete calculations, rather than the other way around.) Does loop quantum gravity count as one?
“I really don’t like the idea that some mathematical objects are “man made” while others are “god made”. It’s fine as a joke, but if one is going to take it seriously it’s either a piece of theology I don’t want to get involved with, or a metaphor for something – and I’d want to know what that something is.”
I don’t know about Kronecker, but I think that nowadays no-one takes that as anything more than an amusing way of saying things. Similarly to Erdos’ way of speaking about maths.
”
Maybe. While Freund and Witten wrote a nice paper on [URL=’http://ncatlab.org/nlab/show/p-adic+string+theory’]adelic string theory[/URL], there really hasn’t been enough progress in this direction for me to take this idea seriously – yet. I think people who like these ideas should work harder to extract results from them. Tim Palmer has a paper that attempts to [URL=’http://arxiv.org/abs/1507.02117′]use the p-adics to get around Bell’s theorem[/URL], but I am not convinced.”
I was just extending the joke above, perhaps I should have put some smilies. I am not familiar but I agree that it doesn’t seem to go any further than just broad ideas. I have only seen this [URL]http://www.math.ucla.edu/~vsv/p-adic%20worldtr.pdf[/URL] .
“And he has a point! The real numbers are a bit more man made than the integers.
”
I really don’t like the idea that some mathematical objects are “man made” while others are “god made”. It’s fine as a joke, but if one is going to take it seriously it’s either a piece of theology I don’t want to get involved with, or a metaphor for something – and I’d want to know what that something is.
”
After all from rationals to reals there is a choice, you can complete them to get the reals or any of the p-adic numbers.
”
Okay, that’s a clear mathematical statement, which is true.
“May be one shouldn’t take reals over any of the p-adics. May be the way to go is to work with the adeles.”
Maybe. While Freund and Witten wrote a nice paper on [URL=’http://ncatlab.org/nlab/show/p-adic+string+theory’]adelic string theory[/URL], there really hasn’t been enough progress in this direction for me to take this idea seriously – yet. I think people who like these ideas should work harder to extract results from them. Tim Palmer has a paper that attempts to [URL=’http://arxiv.org/abs/1507.02117′]use the p-adics to get around Bell’s theorem[/URL], but I am not convinced.
“But is this for all lattice models or only QCD? For QCD the continuum is believed to exist because it is asymptotically free, but for electroweak there is the Landau pole so I think some wish for a lattice regularization to define the standard model non-perturbatively. But the chiral fermion problem seems to be open.”
My remarks were for QCD. I don’t know how [URL=’http://arxiv.org/abs/1406.4088′]the calculation of the neutron/proton mass ratio [/URL]deals with the chiral fermion doubling problem – they call the fermion fields ‘Dirac spinors’, for some reason.
I agree that the existence of the Landau pole makes the Standard Model problematic in the continuum, but it’s also good to remember that it’s heuristic arguments, not theorems, that say the Landau pole is deadly. It’s hard to prove quantum field theories really exist in a rigorous way, but also hard to prove they don’t exist. These are more ‘struggles with the continuum’, which I hope to address in Part 4 of this series.
“For example, in [URL=’https://plus.google.com/117663015413546257905/posts/QsRKWT2VFDt’]computing the neutron/proton mass ratio[/URL] one starts with quantum chromodynamics and then applies a whole battery of analytical methods before doing Monte Carlo integration over fields defined on a discrete lattice, a kind of spacetime grid. Discrete difference equations don’t come into this at all. But my main point is this: nobody working in this subject thinks the lattice actually is spacetime: in fact, the analytical methods are used precisely to understand and correct for the errors introduced by discretization. Without these corrections the computation would be way off.”
But is this for all lattice models or only QCD? For QCD the continuum is believed to exist because it is asymptotically free, but for electroweak there is the Landau pole so I think some wish for a lattice regularization to define the standard model non-perturbatively. But the chiral fermion problem seems to be open.
”
the continuum model breaks down and has to be numerically integrated 99% of the time.
”
When a continuum model really ‘breaks down’, numerical integration can’t revive it.
”
…. reality is really never actually described by differential equations (i.e. by the continuum); reality is always modeled in terms of discrete difference equations.
”
In fact all the most famous laws of physics are given as differential equations or path integrals over infinite-dimensional spaces of fields. These laws are models of reality. We can extract information from these models either by numerical methods, analytical methods, or a combination of the two.
For example, in [URL=’https://plus.google.com/117663015413546257905/posts/QsRKWT2VFDt’]computing the neutron/proton mass ratio[/URL] one starts with quantum chromodynamics and then applies a whole battery of analytical methods before doing Monte Carlo integration over fields defined on a discrete lattice, a kind of spacetime grid. Discrete difference equations don’t come into this at all. But my main point is this: nobody working in this subject thinks the lattice actually is spacetime: in fact, the analytical methods are used precisely to understand and correct for the errors introduced by discretization. Without these corrections the computation would be way off.
In computing the [URL=’https://en.wikipedia.org/wiki/Anomalous_magnetic_dipole_moment#Electron’]magnetic moment of the electron[/URL] one starts with quantum electrodynamics, and there a whole different battery of techniques turns out to be useful. One sums over a large set of Feynman diagrams, each of which is computed with the help of symbolic integration. There’s no discretization whatsoever: all these integrals are done in the continuum. This gives the most accurate calculation ever done in the history of physics: it agrees with experiment to 1 part in a trillion.
Quantum chromodynamics and quantum electrodynamics are in essence quite similar theories. It just happens to be good to use some techniques to do computations in one, and other techniques for the other.
So, I don’t think we can conclude much about whether spacetime is a continuum or discrete, just from the fact that we may prefer to use one method or another to compute things. We have to go out and look.
”
Neither of us were talking about point particles. I was just pointing out how you jumped from a baseball (an actual physical object) to numerical integration (a computer model of an object). ”
Yes, and you have yet to address the point I am trying to make, which is that there is no reason to think that the differential equations used to model the baseball are more fundamental than the difference equations used to model a baseball, and in fact that reality is really never actually described by differential equations (i.e. by the continuum); reality is always modeled in terms of discrete difference equations.
The continuum model is only brought into existence when one makes an scale argument about various quantities, in which one notably never gets, say, an actual infinity.
” The model is not continuous, but that doesn’t prove the baseball isn’t continuous.”
No continuum model accurately models a baseball, at least not in most circumstances (maybe if it is in boring free fall). The continuum model’s regime of validity is always specified using discrete quantities, and the continuum model breaks down and has to be numerically integrated 99% of the time. At any rate it seems like a basic component of science that the accuracy of your model is a reflection of the model’s assumptions. The continuum model’s lack of applicability can even be quantified in terms of various scales (e.g. when the distances are on the order of the diameter of the baseball).
” It depends on your model. For numerical integration, it’s discrete. For analytical or symbolic integration it’s continuous. They both work fine for a falling baseball. One won’t learn much about the ultimate nature of reality from this.”
The baseball is a toy being used here to see how discretization relates to scale and information, which I should hope has something to do with the “ultimate nature of reality.”, as you whimsically put it. The question (it’s not a belief of mine necessarily) regards this general phenomenon of discretization being set by the scales of the system, where it is intuitively obvious how this happens for a baseball, and whether or not this is, as you seem to think, a computationalist’s trick, or whether it actually refers to something true of the “ultimate nature of reality.”
The core ideas are:
1. The continuum breaks down already for a simple classical system being modeled with any degree of seriousness, as evidenced by the fact that we convert our continuum model to a discrete model 99.999% of the time.
2. The basic quantities (time, space) are discretized in accordance with the scales of the system (I previously pointed out why an arbitrarily small timestep makes no sense, for instance). Time is usually “quantized” in terms of the shortest timescale, which then sets limits on spatial resolution, unless you can coarse grain your way out of this difficulty.
3. Point 2 can perhaps be articulated in terms of information.
The catharsis here would presumably be reached by applying the same ideas to something more fundamental and interesting than a baseball, but I don’t personally know how to do this.
“And indeed we have another recent Insights article on exactly that question: [URL]https://www.physicsforums.com/insights/hand-wavy-discussion-planck-length/[/URL]”
I have taken a look at it yesterday, I didn’t have much time at that moment, and had to left the computer to make stuff. I was really concentrated reading at it when I was interrupted and had to leave. That post looks great too, I’ll end the reading just right now, thanks!
“Mainly, it should be small enough that we haven’t seen it.”
Thank you very much John, great insight, and great responses. Thank you for your time.
Regards.
“Wait, you think your point particle with no air resistance is a baseball?”
No, I never said that. Right now we were talking about baseballs, not point particles. You said:
“It doesn’t seem to me that anything is ever continuous; continuous is always an approximation, even in classical mechanics. Take a baseball. Suppose you integrate numerically the simple case where there is just gravity, no air resistance.”
I replied:
“When you speak of numerical integration you’re no longer speaking about a baseball: you’re speaking about a computer program.”
Neither of us were talking about point particles. I was just pointing out how you jumped from a baseball (an actual physical object) to numerical integration (a computer model of an object). The model is not continuous, but that doesn’t prove the baseball isn’t continuous.
”
Space is clearly discrete for the baseball model.
”
It depends on your model. For numerical integration, it’s discrete. For analytical or symbolic integration it’s continuous. They both work fine for a falling baseball. One won’t learn much about the ultimate nature of reality from this.
“The question that arose to me was, if space-time is actually discrete, do you know how small the grid spacing should be?”
Mainly, it should be small enough that we haven’t seen it.
This is a good excuse for me to update [URL=’http://math.ucr.edu/home/baez/distances.html’]my page on distances[/URL]. Quite a while ago I wrote that ##10^{-18}## meters, or an attometer; approximately the shortest distance currently probed by particle physics experiments at CERN (with energies of approximately 100 GeV).”
But the Large Hadron Collider is now running at about 13 TeV or so. So this is about 100 times as much energy… so, using the relativistic relation between energy and momentum, and the quantum relation between momentum and inverse distance, they should be probing physics at distances of about ##10^{-20}## meters.
They’re not mainly looking for a spacetime grid, obviously! But if there a grid this big, we’d probably notice it pretty soon.
So, I’d say smaller than ##10^{-20}## meters.
“According to what we actually know of the laws of physics, is there any upper and/or lower bounding for the space-time grid?
”
The upper bound comes from the fact that we haven’t seen a grid yet.
There’s no real lower bound. We expect quantum gravity effects to kick in at around the Planck length, namely ##10^{-35}## meters. But the argument for this is somewhat handwavy, and there’s certainly no reason to think quantum gravity effects means there’s a grid, either at this scale or any smaller scale.
”
Many people believe that the space grid is Planck’s constant.
”
Really? As you note, that makes no sense, because Planck’s constant is a unit of action, not length.
The [URL=’https://en.wikipedia.org/wiki/Planck_length’]Planck length [/URL]is a unit of length. Ever since Bohr there have been some handwavy arguments that quantum gravity should become important at this length scale. For my own version of these handwavy arguments, check out this thing I wrote:
[LIST]
[*]Length scales, [URL=’http://math.ucr.edu/home/baez/lengths.html#planck_length’]The Planck length[/URL].
[/LIST]
“If you can obtain the entire motion “in principle” and only the practical difficulties of getting measurements at the desired resolution stops us from doing it “in practice”, then the underlying system is (pretty much by definition) continuous at that scale.”
Well if the universe has a finite age/size this would presumably put realistic limits on what can or cannot be computed, but I digress from this point: apart from the fact that your continuum model breaks down at the femtosecond timescale, if you are interested in the ballistics of the baseball, no information about the ballistics is stored at this scale, you’d have to run through thousands of meaningless individual steps before such information began to emerge.
the question is, if at a certain resolution no information about the system is generated, can one really argue that any time elapsed at all? Time is related to how a system changes, which is a matter of what you want to learn about the system. If I’m interested in macroscopic details, a glass of water in thermodynamic equilibrium, while containing many changes at spatial and temporal resolutions I do not care about, is unchanging on the macroscopic scale, and is at this scale time independent.
the whole point I’m meandering towards here is that information, I think, plays an enormous role in this problem, and was not really discussed in this post.
“How about if you integrated at a femtosecond timescale? In principle you could obtain the entire motion, but in practice each step would, individually, produce no information about the system.”
If you can obtain the entire motion “in principle” and only the practical difficulties of getting measurements at the desired resolution stops us from doing it “in practice”, then the underlying system is (pretty much by definition) continuous at that scale.
“Many people believe that the space grid is Plancks constant. But I don’t think there is really any physical reason to believe so”
And indeed we have another recent Insights article on exactly that question: [URL]https://www.physicsforums.com/insights/hand-wavy-discussion-planck-length/[/URL]
“When you speak of numerical integration you’re no longer speaking about a baseball: you’re speaking about a computer program. Of course if you do numerical integration on a computer using time steps, there will be time steps.
I have never seen any actual discretization of space, unless you’re talking about man-made structures like pixels on the computer screens we’re looking at now.”
Wait, you think your point particle with no air resistance is a baseball? It seems to me that neither the differential equation nor the difference equations found on my computer are baseballs, just models of baseballs.
Space is clearly discrete for the baseball model. A femtometer is zero compared to the typical flight distance, so it is below some minimal distance. Worse, your continuum approximation breaks down for distances on the scale of the atoms which make up the baseball.
It seems to me that much of the confusion regarding the continuum arises from assuming that “infinitesimals” and “infinity” have meaningful interpretations outside of notions of characteristic scale in a problem! There is only one kind of infinity, and that’s what happens when you take a number significantly larger than the largest scale of your system, and such a number is indeed finite. The distance from here to the andromeda galaxy is “infinite” compared with the typical baseball flight distance; a wavefunction of an electron prepared in a lab is zero when evaluated at the Andromeda galaxy since this is much larger than say, the width of the potential.
I asked this question to my self last night, perhaps John knows the answer (great responses btw, thank you John, I had a final exam last Friday, so I didn’t had time to read all the details on your responses, but I did yesterday). The question that arised to me was, if space-time is actually discrete, do you know how small the grid spacing should be? According to what we actually know of the laws of physics, is there any upper and/or lower bounding for the space-time grid?
Many people believe that the space grid is Plancks constant. But I don’t think there is really any physical reason to believe so, what is discrete at the plancks lenght is phase space because of the uncertainty principle, not space-time (actually, plancks constant have units of action, not lenght). Space-time is always treated as a continuum in physics. And I didn’t know until now about the struggles with the continuum. But usually, the continuum hypothesis works, and gives reliable physical predictions in most known physics.
“It doesn’t seem to me that anything is ever continuous; continuous is always an approximation, even in classical mechanics. Take a baseball. Suppose you integrate numerically the simple case where there is just gravity, no air resistance.”
When you speak of numerical integration you’re no longer speaking about a baseball: you’re speaking about a computer program. Of course if you do numerical integration on a computer using time steps, there will be time steps.
“Space is also always discretized in terms of the characteristic scales of the system.”
I have never seen any actual discretization of space, unless you’re talking about man-made structures like pixels on the computer screens we’re looking at now.
“The number 473 is just as ‘man-made’ as the numbers π, i, j and k.”
I agree, but let me quote the famous statement by Kronecker:
“God made the integers, all the rest is the work of man.”
“Hi – I’ll be a bit naive here, forgive me, but couldn’t it be that our mathematics is not representing reality, but just a model of it? Nature could be not-continuous by itself.”
We use mathematics to model nature. We find ourselves in a mysterious world and try to understand it – we don’t really know what it’s like. But the discrete and the continuous are abstractions we’ve devised, to help us make sense of things. The number 473 is just as ‘man-made’ as the numbers π, i, j and k.
The universe may be fundamentally mathematical, it may not be – we don’t know. If it is, what kind of mathematics does it use? We don’t know that either. These questions are too hard for now. People have been arguing about them at least since 500 BC when Pythagoras claimed all things are generated from numbers.
If we ever figure out laws of physics that fully describe what we see, we’ll be in a better position to tackle these hard questions. For now I find it more productive to examine the most successful theories of physics and see what issues they raise.
“What happens with for example angular momentum conservation when isotropy is lost?”
Typically it goes away, but if you’re clever you can arrange to preserve it, by choosing particle interactions that conserve it.
”
What would Newtonian physics looks like in this discretized space?
”
The link I sent you is all about ‘lattice Boltzmann gases’, which have particles moving on a lattice and bouncing off each other when they collide. This is one of the earlier papers on this subject, by Steve Wolfram.
On a square lattice in 2 dimensions, you can easily detect macroscopic deviations from isotropy in the behavior of such a gas. On a hexagonal the deviations are much subtler, because hexagonal symmetry invariance implies complete rotation invariance for a number of tensors that are important in fluid flow.
”
Is there any need of a reformulation of Newtons laws or you can recover our macroscopic physics even with a discretized space and the usual, for example Newton’s second law of physics with discrete variables (with out the need of taking the grid spacing tending to zero)?
”
There’s a rather beautiful harmonic oscillator where the particle moves in discrete time steps on a 2d square lattice, but I’m pretty sure the inverse square law is going to be ugly. As you said, you can just think of the lattice as the discretization imposed in numerical analysis by working with numbers that have only a certain number of digits. But in general this is pretty ugly: there’s nothing especially nice about physics where ’roundoff errors’ gradually violate conservation laws.
I find it more interesting to look for discrete models where you can still use a version of Noether’s theorem to get exact conservation laws from symmetries. I had a grad student who wrote his PhD thesis on this:
[LIST]
[*]James Gilliam, [URL=’http://math.ucr.edu/home/baez/thesis_gilliam.pdf’]Lagrangian and Symplectic Techniques in Discrete Mechanics[/URL], Ph.D. thesis, U. C. Riverside, 1996.
[/LIST]
and we published a paper about it:
[LIST]
[*]James Gilliam and John Baez, [URL=’http://math.ucr.edu/home/baez/ca.pdf’]An algebraic approach to discrete mechanics[/URL], Lett. Math. Phys. 31 (1994), 205-212.
[/LIST]
However, while it’s fun, I don’t think it’s the right way to go in physics.
Thanks for your answer John!
What happens with for example angular momentum conservation when isotropy is lost? what would Newtonian physics looks like in this discretized space? Is there any need of a reformulation of Newtons laws or you can recover our macroscopic physics even with a discretized space and the usual, for example Newton’s second law of physics with discrete variables (with out the need of taking the grid spacing tending to zero)? I guess that inertia would hold, as it is related to space homogenity. And I suppose that people working in numerical methods of physics actually use this kind of discretizations every time they make for example a Riemann integral, or use finite difference methods. Is this equivalent to discretizing space in Newtonian physics? and there is any departure from the predictions in continuum space or everything works in the same way?
Perhaps I’m being too incisive about this, after all the post is about the struggles with the continuum and not about the possibility of a discretized space itself. But I thought of it as complementary. If space is not a continuum it has to be discrete, right? or there are other possibilities here?
“Is there any previous work, any attempt on trying to discretize space, or even space time and trying to work the laws of physics, dynamics, classical mechanics, quantum mechanics, and relativity in such a discretized space?
”
Sure, lots.
“I suppose that in the limit of the grid spacing tending to zero one could get the usual mechanics in continuum space or space-time…
”
Yes, for example when they compute the mass of the proton, they discretize spacetime and use lattice gauge theory to calculate the answer – nobody knows any other practical way. But you try to make the grid spacing small to get a good answer.
”
… but I would like to know what kind of physical predictions the discretized space would make, and the possibility to observe experimentally some of those predictions.
Wouldn’t the “nice” properties of space be lost, like homogeneity, isotropy, etc?”
You’d mainly tend to lose isotropy – that is, rotation symmetry. Homogeneity – that is, translation symmetry – will still hold for discrete translations that map your grid to itself. People have looked for violations of isotropy, but perhaps more at large scales than microscopic scales.
What seems cool to me is how cleverly chosen lattice models of fluid dynamics can actually do a darn good job of getting approximate rotation symmetry. For example, in 2 dimensions a square lattice is no good, but a hexagonal lattice is good, thanks to some nice math facts.
Thanks!
I suggest that you look up “Continuity”, “Reversibility”, “Symmetry”, “Commutativity”, “Hermitianness” and “Self-Adjointness” on Wikipedia. They all mean very different things – except for the last two, which are closely related. In my post I was using “symmetric” in a specific technical sense, closely akin to “hermitian”, which is quite different from the general concept of “symmetry” in physics. That’s why I included a link to the definition.
Learning the precise definitions of technical terms is crucial to learning physics. You’re saying a lot of things that don’t make sense, I’m afraid, so I can’t really comment on most of them. That sounds rude, but I’m really hoping a bit of honesty may help here.
Anyway: we need the Hamiltonian H to be self-adjoint for the time evolution operator exp(-itH) to be unitary. And we need time evolution to be unitary for probabilities to add up to 1, as they should.
“At any time, we want ψ to lie in the Hilbert space consisting of square-integrable functions of all the particle’s positions. We can then formally solve Schrödinger’s equation as
ψ(t)=exp(−itH)ψ(0)
where ψ(t) is the solution at time t. But for this to really work, we need H to be a self-adjoint operator on the chosen Hilbert space. The correct definition of [URL=’https://en.wikipedia.org/wiki/Self-adjoint_operator#Self-adjoint_operators’]‘self-adjoint’[/URL] is a bit subtler than what most physicists learn in a first course on quantum mechanics. In particular, an operator can be superficially self-adjoint—the actual term for this is [URL=’https://en.wikipedia.org/wiki/Self-adjoint_operator#Symmetric_operators’]‘symmetric’[/URL]—but not truly self-adjoint.”
Is this because we want the movement of a system in that space to be perfectly reversible? Is Reimannian continuity (if that’s the right term) really about wanting to assume things are equally able or likely to go in any direction in their phase-space from any point?
Basically I am confused here by similar but different terms “Continuity”, “Reversibility”, “Symmetry”, “Commutativity”, “Hermitian-ness” and “Self-Adjoint-ness”. I think the last two may be synonymous, but are these terms just stronger/weaker versions of the same idea, precluding any preferred “direction of the grain” in the phase space?
Thanks for the awesome articles by the way.
The closest I've encountered about grains of space is in loop quantum gravity where space seems to be broken into tiny pieces, maybe a googol of them in a teaspoon. But as I understand it, the pieces are not arranged in a regular grid; they are constantly rearranging themselves, and all their possible arrangements get quantum-superposed so they are all smudged together into something that feels kind of continuous.Is this image even approximately a correct view of the theory?
Is the problem with your Newtonian example due to the implied instantaneous-action-at-a-distance in the fundamental equation (which means the result isn't fully conservative)? At some point you have to modify the equations to allow for changes in the gravitational system to propagate, like Heaviside did in the 1890s, and then you get significantly different results in extreme cases.One final note. Your reply to the God-made/Man-made joke was uncomfortable but you have to remember that discussing the continuum is really the physics equivalent to a "religious" question. I'm an atheist but when I step back, ignore all the equations/models/theories, and look around … I wonder "what in the hell is all this stuff anyway, none of it makes sense". It seems like the only thing we can do is perpetually oscillate between experimental and theoretical advances, never reaching a "ta da, we're done!" moment.
And he has a point! The real numbers are a bit more man made than the integers. After all from rationals to reals there is a choice, you can complete them to get the reals or any of the p-adic numbers. May be one shouldn't take reals over any of the p-adics. May be the way to go is to work with the adeles.
I'm new here, but I thinking you keep breaking down physical objects, you will reach point where breaking it down further will yield no information, but it can be still be theorotically broken down. Would this be discrete or continuous?
It doesn't seem to me that anything is ever continuous; continuous is always an approximation, even in classical mechanics. Take a baseball. Suppose you integrate numerically the simple case where there is just gravity, no air resistance. Can you really make your timestep arbitrarily small? How about if you integrated at a femtosecond timescale? In principle you could obtain the entire motion, but in practice each step would, individually, produce no information about the system, since the change in position would be, relative to the characteristic scales of the problem, zero during each step. There is arguably a minimum time step, which is the smallest step that produces a nonzero change in state relative to the characteristic scales.Space is also always discretized in terms of the characteristic scales of the system.
Hi – I'll be a bit naive here, forgive me, but couldn't it be that our mathematics is not representing reality, but just a model of it? Nature could be not-continuous by itself. I cannot think of a "real" particle being "infinitely close" to another one… And even quantization, or discretizations used in computerized models, aren't real themselves, but just convenient models of natures, useful to make good predictions only up to a certain "extent".I'm afraid we still don't have mathematical models that really represent nature completely (will ever we?) and the difficulties in having converging solutions under certain circumstances might be the result of using inadequate mathematics.Sorry if my point is only loosely defined, but I wonder if this or similar arguments has ever been raised before (as I guess).Thanks John for the excellent presentation of these concepts, anyhow.
Is there any previous work, any attempt on trying to discretize space, or even space time and trying to work the laws of physics, dynamics, classical mechanics, quantum mechanics, and relativity in such a discretized space? I supposse that in the limit of the grid space tending to zero one could get the usual mechanics in continuum space or space-time, but I would like to know what kind of physical predictions the discretized space would make, and the possibility to observe experimentally some of those predictions.