Mathematics Articles

Mathematics as the study of “relationships” rather than “patterns” but they are obviously closely related(!). There is a field of mathematics called “category theory” that is just about as abstract as you can get (the textbook, in the preface, said category theory is often called “abstract nonsense” with no sense of that being derogatory at all).

A category has “objects” and “relations”. The collection of all sets is a category with sets as objects and functions between them as “relations”. The collection of topological spaces is a category with the topological spaces being the objects and continuous functions from one topological space to another being the relations.

Articles for: mathematics

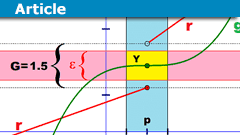
Epsilontic limits and continuity

Epsilontic – Limits and Continuity

1 Comment
/
Abstract I remember that I had some difficulties moving from school mathematics to university mathematics. From what I read on PF through the years, I…
Differential Equation Systems and Nature

Differential Equation Systems and Nature

10 Comments
/
Abstract "Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…
calc precalc

Beginners Guide to Precalculus, Calculus and Infinitesimals

3 Comments
/
Introduction I am convinced students learn Calculus far too late.   In my view, there has never been a good reason for this.In the US, they go through…
what are numbers

What Are Numbers?

7 Comments
/
Introduction When doing mathematics,  we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive.   Going…
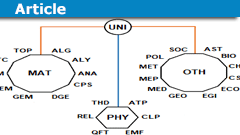
math classifications

Classification of Mathematics by 42 Branches

0 Comments
/
 I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what has…
evariste galois

Évariste Galois and His Theory

0 Comments
/
 * Oct. 25th, 1811  † May 31st, 1832 ... or why squaring the circle is doomed. Galois died in a duel at the age of twenty. Yet, he gave…
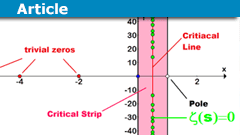
Riemann Hypothesis History

The History and Importance of the Riemann Hypothesis

0 Comments
/
Riemann Hypothesis History The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
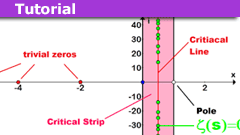
Riemann Hypothesis

The Extended Riemann Hypothesis and Ramanujan’s Sum

2 Comments
/
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line. ERH: All…
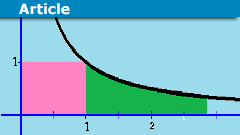
Hyperbola

The Amazing Relationship Between Integration And Euler’s Number

0 Comments
/
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…
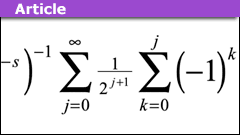
lerch and zeta functions

The Analytic Continuation of the Lerch and the Zeta Functions

0 Comments
/
Introduction In this brief Insight article the analytic continuations of the Lerch Transcendent and Riemann Zeta Functions are achieved via the Euler's…
Integral Representations of Some Special Functions

A Path to Fractional Integral Representations of Some Special Functions

9 Comments
/
Introduction This bit is what new thing you can learn reading this:) As for original content, I only have hope that the method of using the sets $$C_N^n:…
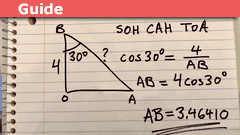
SOHCAHTOA

SOHCAHTOA: Seemingly Simple, Conceivably Complex

7 Comments
/
What is SOHCAHTOA SOHCAHTOA is a mnemonic acronym used in trigonometry to remember the relationships between the sides and angles of right triangles.…
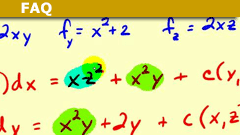
How to Find Potential Functions

How to Find Potential Functions? A 10 Minute Introduction

0 Comments
/
Definition/Summary Given a vector field ##\vec F(x,y,z)## that has a potential function, how do you find it? Equations $$\nabla \phi(x,y,z) = \vec F(x,y,z)$$…
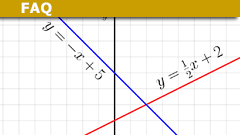
What is a linear equation

What is a Linear Equation? A 5 Minute Introduction

0 Comments
/
Definition/Summary A first-order polynomial equation in one variable, its general form is [itex]Mx+B=0[/itex] where x is the variable. The quantities…
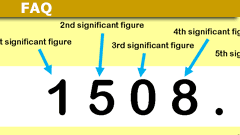
What are significant figures

What are Significant Figures? A 5 Minute Introduction

0 Comments
/
Definition/Summary Significant figures (commonly called "sig figs") are the number of figures (digits) included when rounding-off a number.For example,…
writing proofs

How to Write a Math Proof and Their Structure

1 Comment
/
Proofs in mathematics are what mathematics is all about. They are subject to entire books, created entire theories like Fermat's last theorem, are hard…
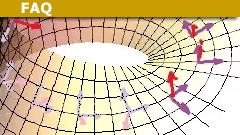
What is a fibre bundle

What is a Fibre Bundle? A 5 Minute Introduction

3 Comments
/
Definition/Summary Intuitively speaking, a fibre bundle is space E which 'locally looks like' a product space B×F, but globally may have a different…
What are real numbers

What is a Real Number? A 5 Minute Introduction

0 Comments
/
Definition of real numbers Real numbers are a comprehensive set of numbers that encompasses all possible values on the number line. They include both…
What is a parabola

What is a Parabola? A 5 Minute Introduction

0 Comments
/
What is a Parabola? A parabola is a U-shaped curve in mathematics that is defined by a specific set of points. It is a fundamental geometric shape that…
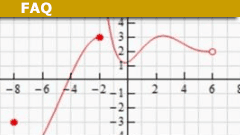
Limit of a Function

What Is a Limit of a Function? A 5 Minute Introduction

0 Comments
/
What is a limit? In mathematics, a limit is a fundamental concept used to describe the behavior of a function or sequence as it approaches a particular…
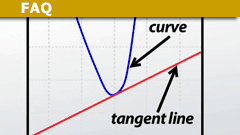
What is a Tangent Line

What is a Tangent Line? A 5 Minute Introduction

0 Comments
/
Definition/Summary The tangent to a curve in a plane at a particular point has the same Gradient as the curve has at that point.More generally, the…
lie algebra representations

Lie Algebras: A Walkthrough The Representations

1 Comment
/
  Part III: Representations  10. Sums and Products. Frobenius began in ##1896## to generalize Weber's group characters and soon investigated…
Lie Algebra Structure

Learn Lie Algebras: A Walkthrough The Structures

2 Comments
/
  Part II: Structures5. Decompositions.Lie algebra theory is to a large extend the classification of the semisimple Lie algebras…
lie algebra basics

Learn Lie Algebras: A Walkthrough The Basics

7 Comments
/
  Part I: Basics 1. Introduction. This article is meant to provide a quick reference guide to Lie algebras: the terminology, important theorems,…
stock options math

Learn a Simplified Synthesis of Financial Options Pricing

19 Comments
/
Financial options (the right to purchase ("call") or sell ("put") stock (or other assets)) at a fixed price at a future date have been around for a long…
selfstudy

How to Self Study Abstract Algebra

4 Comments
/
There are three big parts of mathematics: geometry, analysis, and algebra. In this insight, I will try to give a roadmap towards learning basic abstract…
computers

An Interesting Ramsey Theory Riddle

5 Comments
/
Ramsey theory has its origins in a very nice riddle Consider a party of 6 people. Any two of these 6 will either be meeting each other for the first time…
selfstudyanalysis

How to Self Study Intermediate Analysis Math

14 Comments
/
If you wish to follow this guide, then you should know how to do analysis on ##\mathbb{R}## and ##\mathbb{R}^n##. See my previous insight if you wish to…
MillenniumPrize

Intro to the Millennium Prize Problems

13 Comments
/
IntroductionIn this Insight, I will go over the background information for the Millennium Prize problems and briefly describe three of them. A future…
micro3

An Intro on Real Numbers and Real Analysis

0 Comments
/
It is important to realize that in standard mathematics, we attempt to characterize everything in terms of sets. This means that notions such as natural…
lineartransformations

Learn About Matrix Representations of Linear Transformations

19 Comments
/
Let X and Y be finite-dimensional vector spaces. Let ##T:X\to Y## be a linear transformation. Let ##A=(e_1,\dots,e_n)## and ##B=(f_1,\dots,f_m)## be ordered…
999equals1

Why Do People Say That 1 And .999 Are Equal?

111 Comments
/
Why do people say 1 and 0.999... are equal? Aren't they two different numbers?No, they really are the same number, though this is often very counterintuitive…
999

Is There a Rigorous Proof Of 1 = 0.999…?

102 Comments
/
Yes.First, we have not addressed what 0.999... actually means. So it's best first to describe what on earth the notation [tex]b_0.b_1b_2b_3...[/tex]…

The History and Concept of the Number 0

7 Comments
/
The goal of this FAQ is to clear up the concept of 0 and specifically the operations that are allowed with 0.The best way to start this FAQ is to look…
ADHD studying

How I Overcame Learning Challenges That I Faced Studying Science

22 Comments
/
Introduction For the past few days, during my summer break, I have been intensively self-studying mathematics (namely number theory) for several hours…