What is a Fibre Bundle? A 5 Minute Introduction

Definition/Summary

Intuitively speaking, a fibre bundle is space E which ‘locally looks like’ a product space B×F, but globally may have a different topological structure.

Extended explanation

Definition:

A fibre bundle is the data group $(E, B,\pi, F)$, where $E, B$, and $F$ are topological spaces called the total space, the base space, and the fibre space, respectively and $\pi : E \rightarrow B$ is a continuous surjection, called the projection, or submersion of the bundle, satisfying the local triviality condition.

(We assume the base space B to be connected.)

The local triviality condition states the following:

we require that for any $x \in E$ that there exist an open neighborhood, $U$ of $\pi (x)$ such that $\pi^-1$$(x)$ is homeomorphic to the product space $U×F$ in such a manner as to have $\pi$ carry over to the first factor space of the product.

$U$ is called the trivialization neighborhood, and the set of all $\{U_i, \varphi_i\}$ is called to local trivialization of the bundle, where $\varphi_i:\pi^{-1}\rightarrow U×F$ is a homeomorphism.

Visualization

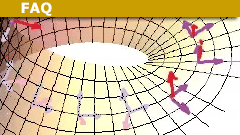
The easiest way of visualizing a fibre bundle is one of the most ordinary household objects: the hairbrush.

In this case the base space $B$is the cylinder, the fibre space $F$ are line fragments, and the projection $\pi$: $E$ $\rightarrow$$B$ takes any point on a given fibre to the point where the fibre attaches to the cylinder.

In the trivial case $E$ is simply the product $B×F$, and the map $\pi$ is just the projection from the product space to the first factor (B). This structure is called the trivial bundle.

Examples

Examples of non-trivial bundles are the Möbius strip and the Klein bottle.

In the case of the Möbius strip, the fibre bundle ‘locally looks like’ the flat Euclidean space R^2, however, the overall topology is markedly different.

A smooth fibre bundle is easily constructed with the above definition using smooth manifolds as $B$, $F$, and $E$ and the given functions are required to be smooth maps.

Generalization of fibre bundles may be given in a variety of ways. The most common is to require that the transition between the local trivial neighbourhoods conform to a certain $G$topological group known as the structure group (or gauge group) acting on the fibre space $F$.

See also: https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/ (esp. part 3)

Comments Thread