Why the Quantum | A Response to Wheeler’s 1986 Paper
Wheeler’s opening statement in his 1986 paper, “How Come the Quantum?” holds as true today as it did then [1]
The necessity of the quantum in the construction of existence: out of what deeper requirement does it arise? Behind it all is surely an idea so simple, so beautiful, so compelling that when — in a decade, a century, or a millennium — we grasp it, we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?
In this Insight, I will answer Wheeler’s question per its counterpart in quantum information theory (QIT), “How come the Tsirelson bound?” Let me start by explaining the Tsirelson bound and its relationship to the Bell inequality, then it will be obvious what that has to do with Wheeler’s question, “How Come the Quantum?” The answer (the Tsirelson bound is a consequence of conservation per no preferred reference frame (NPRF)) may surprise you with its apparent simplicity, but that simplicity belies a profound mystery, as we will see.
The Tsirelson bound is the spread in the Clauser-Horne-Shimony-Holt (CHSH) quantity
\begin{equation}\langle a,b \rangle + \langle a,b^\prime \rangle + \langle a^\prime,b \rangle – \langle a^\prime,b^\prime \rangle \label{CHSH1}\end{equation}
created by quantum correlations. Here, we consider a pair of entangled particles (or “quantum systems” or “quantum exchanges of momentum”). Alice makes measurements on one of the two particles with her measuring device set to ##a## or ##a^\prime## while Bob makes measurements on the other of the two particles with his measuring device set to ##b## or ##b^\prime##. There are two possible outcomes for either Bob or Alice in either of their two possible settings given by ##i## and ##j##. For measurements at ##a## and ##b## we have for the average of Alice’s results multiplied by Bob’s results on a trial-by-trial basis
\begin{equation}\langle a,b \rangle = \sum (i \cdot j) \cdot P(i,j \mid a,b) \label{average}\end{equation}
That’s a bit vague, so let me supply some actual physics. The two entangled states I will use are those which uniquely give rise to the Tsirelson bound [2-4] , i.e., the spin singlet state and the ‘Mermin photon state’ [5]. The spin singlet state is ##\frac{1}{\sqrt{2}} \left(\mid ud \rangle – \mid du \rangle \right)## where ##u##/##d## means the outcome is displaced upwards/downwards relative to the north-south pole alignment of the Stern-Gerlach (SG) magnets (Figure 1).
 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
This state obtains due to conservation of angular momentum at the source as represented by momentum exchange in the spatial plane P orthogonal to the source collimation (“up or down” transverse). This state might be produced by the dissociation of a spin-zero diatomic molecule [6] or the decay of a neutral pi meson into an electron-positron pair [7], processes which conserve spin angular momentum. For more information about the spin singlet state and the spin triplet states, see this Insight.
The Mermin state for photons is ##\frac{1}{\sqrt{2}} \left(\mid VV \rangle + \mid HH \rangle \right)## where ##V## means the there is an outcome (photon detection) behind one of the coaligned polarizers and ##H## means there is no outcome behind one of the co-aligned polarizers. This state obtains due to conservation of angular momentum at the source as represented by momentum exchange along the source collimation (“yes” or “no” longitudinal). Dehlinger and Mitchell created this state by laser inducing spontaneous parametric downconversion in beta barium borate crystals [8], a process that conserves spin angular momentum as represented by the polarization of the emitted photons. At this point we will focus the discussion on the spin single state for total anti-correlation, since everything said of that state can be easily transferred to the Mermin photon state.
Let us investigate what Alice and Bob discover about these entangled states in the various contexts of their measurements (Figure 2). Alice’s detector responds up and down with equal frequency regardless of the orientation ##\alpha## of her SG magnet. This is in agreement with the relativity principle, aka “no preferred reference frame” (NPRF), where different SG magnet orientations relative to the source constitute different “reference frames” in quantum mechanics just as different velocities relative to the source constitute different “reference frames” in special relativity (see this Insight).
Figure 2. Alice and Bob making spin measurements in the xz plane on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors.
Bob observes the same regarding his SG magnet orientation ##\beta##. Thus, the source is rotationally invariant in the spatial plane P orthogonal to the source collimation. When Bob and Alice compare their outcomes, they find that their outcomes are perfectly anti-correlated (##ud## and ##du## with equal frequency) when ##\alpha – \beta = \theta = 0## (Figure 3). This is consistent with conservation of angular momentum per classical mechanics between the pair of detection events (again, this fact defines the state). The degree of that anti-correlation diminishes as ##\theta \rightarrow \frac{\pi}{2}## until it is equal to the degree of correlation (##uu## and ##dd##) when their SG magnets are at right angles to each other. In other words, whenever the SG magnets are orthogonal to each other anti-correlated and correlated outcomes occur with equal frequency, i.e., conservation of angular momentum in one direction is independent of the angular momentum changes in any orthogonal direction. Thus, we wouldn’t expect to see more correlation or more anti-correlation based on conservation of angular momentum for transverse results in the plane P when the SG magnets are orthogonal to each other. As we continue to increase the angle ##\theta## beyond ##\frac{\pi}{2}## the anti-correlations continue to diminish until we have totally correlated outcomes when the SG magnets are anti-aligned. This is also consistent with conservation of angular momentum, since the totally correlated results when the SG magnets are anti-aligned represent momentum exchanges in opposite directions in the plane P just as when the SG magnets are aligned, it is now simply the case that what Alice calls up, Bob calls down and vice-versa.
The counterpart for the Mermin photon state is simply that angular momentum conservation is evidenced by ##VV## or ##HH## outcomes for coaligned polarizers. When the polarizers are at right angles you have only ##VH## and ##HV## outcomes, which is still totally consistent with conservation of angular momentum as ‘not ##H##’ implies ##V## and vice-versa [8]. In other words, a polarizer does not have a ‘north-south’ distinction (longitudinal rather than transverse momentum exchange). In particular, having rotated either or both polarizers by ##\pi## one should obtain precisely ##VV## or ##HH## outcomes again.
Nothing is particularly mysterious about the entangled states for electron spin or photon polarization described here so far because we have been thinking as if conservation of angular momentum holds for each experimental trial, as in classical mechanics. Truth is, since Alice and Bob can only measure +1 or -1 (quantum exchange of momentum per NPRF), we can only get conservation of angular momentum in any particular trial when their SG magnets/polarizers are co-aligned. And, we cannot use classical probability theory to account for the conservation of angular momentum on average.
In particular, the probability that Alice and Bob will measure ##uu## or ##dd## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityuu}\end{equation}
And, the probability that Alice and Bob will measure ##ud## or ##du## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityud}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##u##) and -1 (##d##) gives Eq. (\ref{CHSH1}) of
\begin{equation}-\cos(a – b) -\cos(a – b^\prime) -\cos(a^\prime – b) +\cos(a^\prime – b^\prime) \label{CHSHspin}\end{equation}
Choosing ##a = \pi/4##, ##a^\prime = -\pi/4##, ##b = 0##, and ##b^\prime = \pi/2## minimizes Eq. (\ref{CHSHspin}) at ##-2\sqrt{2}## (the Tsirelson bound).
Likewise, for the Mermin photon state we have
\begin{equation}P_{VV} = P_{HH} = \frac{1}{2} \mbox{cos}^2 \left(\alpha – \beta \right) \label{probabilityVV}\end{equation}
and
\begin{equation}P_{VH} = P_{HV} = \frac{1}{2} \mbox{sin}^2 \left(\alpha – \beta \right) \label{probabilityVH}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##V##) and -1 (##H##) gives Eq. (\ref{CHSH1}) of
\begin{equation}\cos2(a – b) +\cos2(a – b^\prime) +\cos2(a^\prime – b) -\cos2(a^\prime – b^\prime) \label{CHSHmermin}\end{equation}
Using ##a = \pi/8##, ##a^\prime = -\pi/8##, ##b = 0##, and ##b^\prime = \pi/4## maximizes Eq. (\ref{CHSHmermin}) at ##2\sqrt{2}## (the Tsirelson bound). So, we have two mysteries.
First, as explained by Mermin [5], suppose you restrict Alice and Bob’s measurement angles ##\alpha## and ##\beta## to three possibilities, setting 1 is ##0^o##, setting two is ##120^o##, and setting three is ##-120^o##. Eq. (\ref{probabilityud}) says the probability of getting opposite results is 1 when ##\alpha = \beta## (1/2 ##ud## and 1/2 ##du##) and 1/4 otherwise (1/8 ##ud## and 1/8 ##du##). Now, if the source emits particles with definite properties that account for their outcomes in the three possible measurement settings, and we have to get total anti-correlation for like settings, then the particles’ so-called “instruction sets” must be opposite for each of the three settings. For example, suppose we have 1(##u##)2(##u##)3(##d##) for Alice and 1(##d##)2(##d##)3(##u##) for Bob. That guarantees the total anti-correlation for like settings, i.e., 11 gives ##ud##, 22 gives ##ud##, and 33 gives ##du##. And, for unlike settings we get anti-correlation in two combinations, i.e., 12 gives ##ud## and 21 gives ##ud##. In fact, for any instruction set with two ##u## and one ##d## we get anti-correlation for unlike settings in two of the six possible unlike combinations (12,13,21,23,31,32). The only other way to make a pair of instruction sets is to have one with all ##u## and the other with all ##d##. In that case, we get anti-correlation for all six unlike combinations. That means the instruction sets necessary to guarantee anti-correlation for like settings lead to an overall anti-correlation greater than 2/6 for unlike settings, which is greater than the quantum probability for anti-correlation in unlike settings of 1/4. This is Mermin’s version of the Bell inequality [9] (fraction of anti-correlated outcomes for unlike settings must be greater than 2/6) and the manner by which it is violated by quantum correlations (1/4 is less than 2/6). Thus, instruction sets (“counterfactual definiteness”) assumed by classical probability theory cannot account for quantum correlations in this case.
The counterpart to this for the CHSH quantity is that classical correlations give a range of -2 to 2 for the CHSH quantity (“CHSH-Bell inequality”). And, as we saw above, the Tsirelson bound violates the CHSH-Bell inequality. Experiments show that the quantum results can be achieved (violating the Bell inequality), ruling out an explanation of these correlated momentum exchanges via instruction sets per classical probability theory.
The second mystery is that even in cases where we don’t violate the Bell inequality, e.g., ##a = b = 0## and ##a^\prime = b^\prime = \pi/2## which give a CHSH value of 0, we still have conservation of angular momentum. Why is that mysterious? Well, it’s not when the SG magnets are co-aligned, since in those cases we always get a +1 outcome and a -1 outcome for a total of zero. But, in trials where ##\alpha – \beta = \theta## does not equal zero, we need either Alice or Bob, at minimum, to measure something less than 1 to conserve angular momentum. For example, if Alice measures +1, then Bob must measure ##-\cos{\theta}## to conserve angular momentum for that trial. But, again, Alice and Bob only measure +1 or -1 (quantum exchange of momentum per NPRF, which uniquely distinguishes the quantum joint distribution from its classical counterpart [10]), so that can’t happen (Figure 4). What does happen? We conserve angular momentum on average in those trials.
It is easy to see how this follows by starting with total angular momentum of zero for binary (quantum) outcomes +1 and -1 (I am suppressing the factor of ##\hbar/2## and I’m referring to the spin singlet state here [11], Figure 3).

Figure 3. Outcomes (yellow dots) in the same reference frame, i.e., outcomes for the same measurement (blue arrows represent SG magnet orientations), for the spin singlet state explicitly conserve angular momentum.
Alice and Bob both measure +1 and -1 results with equal frequency for any SG magnet angle (NPRF) and when their angles are equal they obtain different outcomes giving total angular momentum of zero. The case (a) result is not difficult to understand via conservation of angular momentum, because Alice and Bob’s measured values of spin angular momentum cancel directly when ##\alpha = \beta##, that defines the spin singlet state. But, when Bob’s SG magnet is rotated by ##\alpha – \beta = \theta## relative to Alice’s, the situation is not as clear (Figure 6).
In classical physics, one would say the projection of the angular momentum vector of Alice’s particle ##\vec{S}_A = +1\hat{a}## along ##\hat{b}## is ##\vec{S}_A\cdot\hat{b} = +\cos{(\theta)}## where again ##\theta## is the angle between the unit vectors ##\hat{a}## and ##\hat{b}## (Figure 2). From Alice’s perspective, had Bob measured at the same angle, i.e., ##\beta = \alpha##, he would have found the angular momentum vector of his particle was ##\vec{S}_B = -1\hat{a}##, so that ##\vec{S}_A + \vec{S}_B = \vec{S}_{Total} = 0##. Since he did not measure the angular momentum of his particle at the same angle, he should have obtained a fraction of the length of ##\vec{S}_B##, i.e., ##\vec{S}_B\cdot\hat{b} = -1\hat{a}\cdot\hat{b} = -\cos{(\theta)}## (Figure 4).

Figure 4. The projection of the angular momentum of Bob’s particle ##\vec{S}_B## along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum due to NPRF.
Of course, Bob only ever obtains +1 or -1 per NPRF, so Bob’s outcomes can only average the required ##-\cos{(\theta)}##. Thus, NPRF dictates
\begin{align*}
P_{uu} + P_{ud} & = \frac {1}{2} \\
P_{ud} + P_{dd} & = \frac {1}{2},
\end{align*}
These equations now allow us to uniquely solve for the joint probabilities
\begin{equation}
P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\theta}{2} \right) \label{QMjointLike}
\end{equation}
and
\begin{equation}
P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\theta}{2} \right) \label{QMjointUnlike}
\end{equation}
\begin{equation}
\overline{BA-} = 2P_{du}(+1) + 2P_{dd}(-1) = \cos (\theta) \label{BA-}
\end{equation}
Using Eqs. (\ref{BA+}) and (\ref{BA-}) in Eq. (\ref{consCorrel}) we obtain
\begin{equation}
\langle \alpha,\beta \rangle = \frac{1}{2}(+1)_A(-\mbox{cos} \left(\theta\right)) + \frac{1}{2}(-1)_A(\mbox{cos} \left(\theta\right)) = -\mbox{cos} \left(\theta\right) \label{consCorrel2}
\end{equation}
which is precisely the correlation function for a spin singlet state found using the joint probabilities per quantum mechanics. To see that we simply use Eqs. (\ref{probabilityuu}) and (\ref{probabilityud}) in Eq. (\ref{average}) to get
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)(-1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(+1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) +\\ &(+1)(+1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(-1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \\ &= -\mbox{cos} \left(\alpha – \beta \right) = -\mbox{cos} \left(\theta \right)
\end{split}
\label{correl}\end{equation}
Thus, “average-only” conservation maps beautifully to our classical expectation (Figures 6 & 7). Since the angle between SG magnets ##\theta## is twice the angle between Hilbert space measurement bases, this result easily generalizes to conservation per NPRF of whatever the measurement outcomes represent when unlike outcomes entail conservation in the symmetry plane [15] (see this Insight on the Bell spin states). However, again, none of the formalism of quantum mechanics is used in obtaining Eq. (\ref{consCorrel2}) or our quantum state Eqs. (\ref{QMjointLike}) & (\ref{QMjointUnlike}). In deriving the quantum correlation function and quantum state in this fashion, we assumed only NPRF.For the Mermin photon state, conservation of angular momentum is established by ##V## (designated by +1) and ##H## (designated by -1) results through a polarizer. When the polarizers are co-aligned Alice and Bob get the same results, half pass and half no pass. Thus, conservation of angular momentum is established by the intensity of the electromagnetic radiation applied to binary outcomes for various polarizer orientations. As with spin angular momentum, this is classical thinking applied to binary outcomes per conservation of angular momentum. Again, grouping Alice’s results into +1 and -1 outcomes we see that she would expect to find ##[\mbox{cos}^2\theta – \mbox{sin}^2\theta]## at ##\theta## for her +1 results and ##[\mbox{sin}^2\theta – \mbox{cos}^2\theta]## for her -1 results. Since Bob measures the same thing as Alice for conservation of angular momentum, those are Bob’s averages when his polarizer deviates from Alice’s by ##\theta##. Therefore, the correlation of results for conservation of angular momentum is given by
\begin{equation}\langle \alpha,\beta \rangle =\frac{(+1_A)(\mbox{cos}^2\theta – \mbox{sin}^2\theta)}{2} + \frac{(-1_A)(\mbox{sin}^2\theta – \mbox{cos}^2\theta)}{2} = \cos{2\theta} \label{merminconserve}\end{equation}
which is precisely the correlation given by quantum mechanics.As before, we need to find ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## so we need four independent conditions. Normalization and ##P_{VH} = P_{HV}## are the same as for the spin case. The correlation function
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)_A(+1)_BP_{VV} + (+1)_A(-1)_BP_{VH} + \\&(-1)_A(+1)_BP_{HV} + (-1)_A(-1)_BP_{HH}\label{correlFn2}
\end{split}
\end{equation}
along with our conservation principle represented by Eq. (\ref{merminconserve}) give
\begin{equation}
P_{VV} – P_{VH} = -\frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
and
\begin{equation}
P_{HV} – P_{HH} = \frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
Solving these four equations for ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## gives precisely Eqs. (\ref{probabilityVV}) & (\ref{probabilityVH}).Notice that since the angle between polarizers ##\alpha – \beta## equals the angle between Hilbert space measurement bases, this result immediately generalizes to conservation per NPRF of whatever the outcomes represent when like outcomes entail conservation in the symmetry plane [15] (again, see this Insight on the Bell spin states).Since the quantum correlations violate the Bell inequality to the Tsirelson bound and satisfy conservation per NPRF while the classical correlations do not violate the Bell inequality, the classical correlations do not satisfy conservation per NPRF. Experiments of course tell us that Nature obeys the quantum correlations and therefore the conservation per NPRF.

Figure 5. A spatiotemporal ensemble of 8 experimental trials for the Bell spin states showing Bob’s outcomes corresponding to Alice‘s ##+1## outcomes when ##\theta = 60^\circ##. Angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{60^\circ}=\frac{1}{2}##). It is impossible for angular momentum to be conserved explicitly in each trial since the measurement outcomes are binary (quantum) with values of ##+1## (up) or ##-1## (down) per no preferred reference frame. The conservation principle at work here assumes Alice and Bob’s measured values of angular momentum are not mere components of some hidden angular momentum with variable magnitude. That is, the measured values of angular momentum are the angular momenta contributing to this conservation.
Figure 6. For the spin singlet state (S = 0). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from –1 (totally down, arrow bottom) to 0 to +1 (totally up, arrow tip). This obtains per conservation of angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of angular momentum on average, because they only measure +1/-1, never a fractional result. Thus, just as with the light postulate of special relativity, we see that no preferred reference frame leads to counterintuitive results (see this Insight).
Figure 7. The situation is similar for the spin triplet states where outcomes agree for the same measurement in the plane containing the conserved angular momentum vector (S = 1). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to –1 (totally down, arrow bottom). This obtains per conservation of angular momentum on average in the plane containing the S = 1 spin angular momentum in accord with no preferred reference frame. See this Insight for details.
So, while conservation per NPRF sounds like a very reasonable constraint on the distribution of quantum exchange of momentum (+1 or -1, no fractions), we still do not have any causal mechanism to explain the outcomes of any particular trial when the SG magnets/polarizers are not co-aligned (Figure 4). And, as I showed above, we cannot use instruction sets per classical probability theory to account for the Tsirelson bound needed to explain the conservation of angular momentum on average. Thus, while we have a very reasonable constraint on the distribution of entangled quantum exchanges (conservation of angular momentum), that constraint has no compelling dynamical counterpart, i.e., no consensus causal mechanism to explain the outcome of any particular trial when the SG magnets/polarizers are not co-aligned and no counterfactual definiteness to explain why conservation of angular momentum is conserved on average. What we have is a “principle” account of entanglement and the Tsirelson bound (see this Insight). I will return to this point after showing how so-called “superquantum correlations” fail to satisfy this constraint as well.
There are QIT correlations that not only violate the Bell inequality, but also violate the Tsirelson bound. Since these correlations violate the Tsirelson bound, they are called “superquantum correlations.” The reason QIT considers these correlations reasonable (no known reason to reject their possibility) is because they do not violate superluminal communication, i.e., the joint probabilities don’t violate the no-signaling condition
\begin{equation}\begin{split}P(A \mid a\phantom{\prime},b\phantom{\prime}) &= P(A \mid a\phantom{\prime}, b^\prime)\\
P(A \mid a^\prime,b\phantom{\prime}) &= P(A \mid a^\prime, b^\prime)\\
P(B \mid a\phantom{\prime},b\phantom{\prime}) &= P(B \mid a^\prime, b\phantom{\prime})\\
P(B \mid a\phantom{\prime},b^\prime) &= P(B \mid a^\prime, b^\prime )\end{split}\label{nosig}\end{equation}
This means Alice and Bob measure the same outcomes regardless of each other’s settings. If this wasn’t true, Alice and Bob would notice changes in the pattern of their outcomes as the other changed their measurement settings. Since the measurements for each trial can be spacelike separated that would entail superluminal communication.
The Popescu-Rohrlich (PR) joint probabilities
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
produce a value of 4 for Eq. (\ref{CHSH1}), the largest of any no-signaling possibilities. Thus, the QIT counterpart to Wheeler’s question, “How Come the Quantum?” is “Why the Tsirelson bound?” [12-14]. In other words, is there any compelling principle that rules out superquantum correlations as conservation of angular momentum ruled out classical correlations? Let us look at Eq. (\ref{PRcorr}) in the context of our spin singlet and Mermin photon states. Again, we will focus the discussion on the spin singlet state and allude to the obvious manner by which the analysis carries over to the Mermin photon state.
The last PR joint probability certainly makes sense if ##a^\prime = b^\prime##, i.e., the total anti-correlation implying conservation of angular momentum, so let us start there. The third PR joint probability makes sense for ##b = \pi + b^\prime##, where we have conservation of angular momentum with Bob having flipped his coordinate directions. Likewise, then, the second PR joint probability makes sense for ##a = \pi + a^\prime##, where we have conservation of angular momentum with Alice having flipped her coordinate directions. All of this is perfectly self consistent with conservation of angular momentum as we described above, since ##a^\prime## and ##b^\prime## are arbitrary per rotational invariance in the plane P. But now, the first PR joint probability is totally at odds with conservation of angular momentum. Both Alice and Bob simply flip their coordinate directions, so we should be right back to the fourth PR joint probability with ##a^\prime \rightarrow a## and ##b^\prime \rightarrow b##. Instead, the first PR joint probability says that we have total correlation (maximal violation of conservation of angular momentum) rather than total anti-correlation per conservation of angular momentum, which violates every other observation. In other words, the set of PR observations violates conservation of angular momentum in a maximal sense. To obtain the corresponding argument for angular momentum conservation per the correlated outcomes of the Mermin photon state, simply start with the first PR joint probability and show the last PR joint probability maximally violates angular momentum conservation.
To find the degree to which superquantum correlations violate our constraint, replace the first PR joint probability with
\begin{equation}\begin{split}&p(1,1 \mid a,b) = C \\
&p(-1,-1 \mid a, b) = D \\
&p(1,-1 \mid a,b) = E \\
&p(-1,1 \mid a, b) = F \\ \end{split} \label{PRcorrMod}\end{equation}
The no-signaling condition Eq. (\ref{nosig}) in conjunction with the second and third PR joint probabilities gives ##C = D## and ##E = F##. That in conjunction with normalization ##C + D + E + F =1## and P(anti-correlation) + P(correlation) = 1 means total anti-correlation (##E = F = 1/2##, ##C = D = 0##) is the conservation of angular momentum per the quantum case while total correlation (##E = F = 0##, ##C = D = 1/2##) is the max violation of conservation of angular momentum per the PR case. To get the corresponding result for the Mermin photon state, simply replace the last PR joint probability in analogous fashion, again with ##\theta = \pi##. In that case, the PR joint probabilities violate conservation of angular momentum with total anti-correlation while the Mermin photon state satisfies conservation of angular momentum with total correlation. Thus, we have a spectrum of superquantum correlations all violating conservation of angular momentum.
So, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a ‘causal influence’ or hidden variables acting on a trial-by-trial basis to account for that conservation. That is the essence of a “principle theory.” Indeed, the kinematic structure (Minkowski spacetime) of special relativity and the kinematic structure (qubit Hilbert space) of quantum mechanics both follow from NPRF, so we now know that quantum mechanics is on par with special relativity as a principle theory (again, see this Insight).
Therefore, my answer to QIT’s version of Wheeler’s question is
The Tsirelson bound obtains because of conservation per no preferred reference frame.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation per NPRF [16,17,18]) to dispel the mystery of entanglement and answer Wheeler’s question depends on whether or not you can accept the fundamentality of a principle explanation via patterns in both space and time (see this Insight). While we have a compelling 4D constraint (who would argue with conservation per NPRF?) for our adynamical explanation, we do not have a compelling dynamical counterpart. That is, we do not have a consensus, causal mechanism to explain outcomes on a trial-by-trial basis when the SG magnets/polarizers are not co-aligned, and we cannot use counterfactual definiteness per classical probability theory to account for the fact that we conserve angular momentum on average. So, perhaps we do not need new physics to rise to Wilczek’s challenge [19].
To me, ascending from the ant’s-eye view to the God’s-eye view of physical reality is the most profound challenge for fundamental physics in the next 100 years.
[Note: “God’s-eye view” simply means the blockworld, block universe, “all-at-once”, or 4D view like that of Minkowski spacetime, there is no religious connotation.] Since special relativity already supports that view, perhaps we should accept that adynamical explanation is fundamental to dynamical explanation, so that not all adynamical explanations have dynamical counterparts [20]. In that case, “we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?” [1]
References
- Wheeler, J.A.: How Come the Quantum?, New Techniques and Ideas in Quantum Measurement Theory 480(1), 304–316 (1986).
- Cirel’son, B.S.: Quantum Generalizations of Bell’s Inequality, Letters in Mathematical Physics 4, 93–100 (1980).
- Landau, L.J.: On the violation of Bell’s inequality in quantum theory, Physics Letters A 120(2), 54–56 (1987).
- Khalfin, L.A., and Tsirelson, B.S.: Quantum/Classical Correspondence in the Light of Bell’s Inequalities, Foundations of Physics 22(7), 879–948 (1992).
- Mermin, N.D.: Bringing home the atomic world: Quantum mysteries for anybody, American Journal of Physics 49(10), 940–943 (1981).
- Bohm, D.: Quantum Theory, Prentice-Hall, New Jersey (1952).
- La Rosa, A.: Introduction to Quantum Mechanics, Chapter 12
- Dehlinger, D., and Mitchell, M.W.: Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory, American Journal of Physics 70(9), 903–910 (2002).
- Bell, J.: On the Einstein-Podolsky-Rosen paradox, Physics 1, 195–200 (1964).
- Garg, A., and Mermin, N.D.: Bell Inequalities with a Range of Violation that Does Not Diminish as the Spin Becomes Arbitrarily Large, Physical Review Letters 49(13), 901–904 (1982).
- Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
- Bub, J.: Bananaworld: Quantum Mechanics for Primates, Oxford University Press, Oxford, UK (2016).
- Bub, J.: Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B, 241–266 (2004).
- Bub, J.: Why the Tsirelson bound?, in The Probable and the Improbable: The Meaning and Role of Probability in Physics, eds. Meir Hemmo and Yemima Ben-Menahem, Springer, Dordrecht, 167–185 (2012).
- Weinberg, S.: The Trouble with Quantum Mechanics (2017).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Kohler, I: Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum, Entropy 21(7), 692 (2019).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D.: Answering Mermin’s challenge with conservation per no preferred reference frame, Scientific Reports 10, 15771 (2020).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s, Entropy 23(1), 114 (2021).
- Wilczek, F.: Physics in 100 Years, Physics Today 69(4), 32–39 (2016).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford University Press, Oxford, UK (2018).
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018).


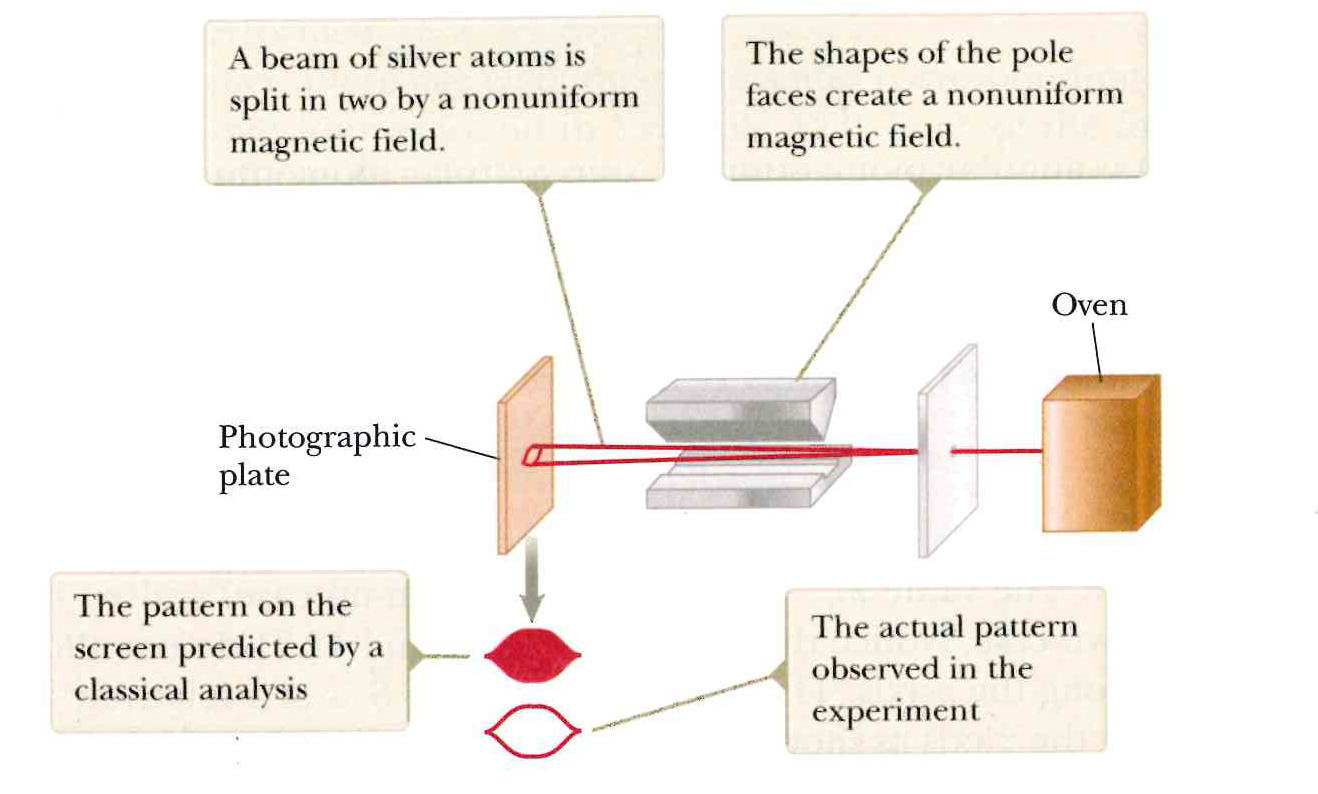 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.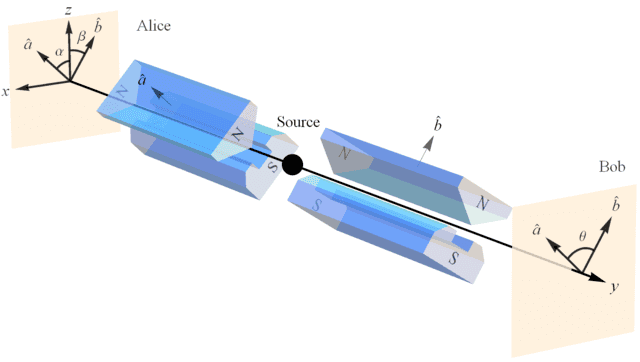








No, we have to interpret the complex coefficients of each term in the superposition as probability amplitudes for the measurement result described by that particular term to be observed when we make a measurementIf you describe the measurement process itself as a quantum-mechanical interaction, then what you will find is that the combination measured-system-plus-measuring-device-plus-environment will evolve into a superposition of a number of possibilities.
You have a particle that is in a superposition of, say, spin-up with amplitude ##alpha## and spin-down with amplitude ##beta##. Then under unitary evolution, the whole shebang will evolve into a superposition of
The amplitude for the first possibility will be ##alpha## and the the amplitude for the second possibility will be ##beta##. You can interpret this as "there is a probability of ##|alpha|^2## for the first possibility and a probability of ##|beta|^2## of the second possibility. But to say that it requires another measurement of the measuring device before you can assign probabilities seems like it leads to an infinite regress.
No idea what principles the "collapse postulate" contradicts. I don't understand the wave function as referring to something physically real.The instantaneous-collapse postulate obviously contradicts Einstein causality.
I'm also not sure whether it's clear what you mean by "something physically real". The wave function has a clear probabilistic meaning, referring to the expected statistics when doing measurements in ensembles of correspondingly prepared quantum systems. So it has a real meaning in the sense that you can observe, what it predicts, namely the statistics for the outcome of observations on ensembles of equally prepared quantum systems.
If we are to give a probabilistic interpretation to this situation, we have to give probabilities to elements of a superposition.No, we have to interpret the complex coefficients of each term in the superposition as probability amplitudes for the measurement result described by that particular term to be observed when we make a measurement. That is not the same as saying that the superposition itself–the state with all the terms in it, each with its amplitude–is a state in which each term has some probability of being real. A superposition is a state in which all of the terms are real. If we are trying to describe a situation where only one of the states is real, we just don't know which, that's a mixture, not a superposition.
I'm talking here about a minimalist interpretation, in which there is no collapse hypothesis.No, but, as you have been insisting all along, there is still a distinction between states that are "macroscopically distinguishable" and states that aren't.
I think you have to say that a superposition of macroscopically distinguishable alternatives implies that one of the alternatives is real, and which one is purely probabilistic.No, you have to say that, once the alternatives become macroscopically distinguishable, only one of the alternatives is real, and therefore you cannot describe the system as being in a superposition any more. You have to apply the Born rule to calculate the probabilities of each alternative being real, and then you treat the actual state of the system as being the eigenstate corresponding to whichever alternative is measured to be real.
I think this is a misuse of the term "superposition". That term never means that "the system is either in this state or that state, with such-and-such probability". That is a "mixture".I'm disagreeing with that. In the case where you have a superposition of macroscopically distinguishable alternatives, it DOES mean that.
If the state of the universe starts off as a pure state, then it will evolve into another pure state. If in the history of the universe, we perform measurements, then that pure state will involve a superposition of some states in which the measurement yielded this result, and some states in which the measurement result yielded that result. If we are to give a probabilistic interpretation to this situation, we have to give probabilities to elements of a superposition.
[edit]I'm talking here about a minimalist interpretation, in which there is no collapse hypothesis. If you have no collapse hypothesis, and you still want to preserve the probabilistic predictions of QM, I think you have to say that a superposition of macroscopically distinguishable alternatives implies that one of the alternatives is real, and which one is purely probabilistic.
It's not true in general that a superposition of two states means "the system is either in this state or that state, with such-and-such probability". It's only true if it's a superposition of macroscopically distinguishable states.I think this is a misuse of the term "superposition". That term never means that "the system is either in this state or that state, with such-and-such probability". That is a "mixture".
The question is whether a superposition (defined as I just have) of macroscopically distinguishable states is even possible. The MWI says it is; a collapse interpretation says it isn't (collapse always removes all but one term in the superposition before that happens).
That's a problem only if you believe in the necessity of the collapse postulate, which is not necessary at all. It even contradicts fundamental principles (relativistic spacetime structure) and it's almost always not what happens in real experiments.No idea what principles the "collapse postulate" contradicts. I don't understand the wave function as referring to something physically real.
Axiom 4 doesn't claim anything about the specialty of observations in contradistinction to any other interactionThat seems completely wrong. Other interactions don't have the property that the interaction results in an eigenvalue of some operator, with some particular probability.
Axiom 4 doesn't claim anything about the specialty of observations in contradistinction to any other interaction. It just tells the meaning of the formal objects of the theory when applied to real-world phenomena. That's what's necessarily done in all theories, including classical mechanics. There you also start from abstract objects like points on a fibre bundle representing spacetime when dealing with Newtonian mechanics or a affine Minkowski space when dealing with special relativistic mechanics. The relation to the observations is, admittedly, more direct in this case, and you don't have to deal with probabilities necessarily to begin with, but neither in quantum theory nor in classical physics is anything special about observations or measurement. In both cases the interaction between measurement device and measured object follows the general laws of nature as discovered by physics.
There's nothing special about them.Then why is there an axiom that only applies to observations/measurements? (Axiom 4)
What you're saying just seems like a contradiction.
I give up.I think that's appropriate, because what you're defending is just indefensible. You have an interpretation that makes an essential difference between observations and other kinds of interaction. It has no physical content without that distinction. Yet you're denying that it makes such a distinction. It seems like a contradiction.
I give up. Obviously we have a very different perception by the meaning of the word "distinction". For me observations take place via the usual physical laws. There's nothing special about them. Obviously for you there is some distinction, I'm not able to comprehend. You don't tell me what this distinction might be, but just state it about axioms where I don't even mention measurements. Usually one doesn't even mention measurments in the formulation of Newton's laws either, because what a measurement is is not within the axioms but given by what observers do in the lab.
Of course, besides the dynamical laws there are kinematical laws (you have to formulate first). I thought, the quantum postulates of the minimal interpretation are well-known enough, as we have discussed this over and over in the past. Obviously that's not the case. So here are the kinematical postulates again.
(1) A quantum system is defined by an Hilbert space and a realization of an algebra of observables.
(2) Observables are represented by self-adjoint operators, densely defined on Hilbert space (which implies that their (generalized) eigenstates form a complete set). The possible values of the so represented observables are given by the spectrum of these operators.
(3) States are represented by a self-adjoint positive semi definite operator ##hat{rho}##.
(4) The probability for finding an observable ##A## to have the value ##a## in the spectrum of its representing operator ##hat{A}## is given by
$$P(a|hat{rho})=sum_{beta} langle a,beta|hat{rho}|a,beta rangle.$$
Here, ##beta## for each ##a## label the orthonormalized eigenvectors of ##hat{A}## with eigenvalue ##a## (of course ##beta## can also be continuous, but that's only a mathematical detail, unimportant for our discussion).Yes, assumption number (4) makes a distinction between observations and other interactions. It's right there in the postulates. Yet you deny that it makes such a distinction. It really seems that you believe contradictory things.
That's a problem only if you believe in the necessity of the collapse postulate, which is not necessary at all.I don't see how there is any physical content to the minimal interpretation without the collapse hypothesis. You measure an electron's spin relative to the z-axis. You find it's spin-up. Does that mean that your measurement device is in the state of "having measured a spin-up electron", or not?
I assume that it does mean that. Then you have a contradiction. On the one hand, you computed the state of the measurement device using quantum mechanics, and you found that it's entangled, and has no state of its own, but that the entire system is in a superposition of "the electron is spin-up and the measurement device measured spin-up and the environment is whatever is appropriate for a measurement device that measured spin-up" and "the electron is spin-down and all that entails". On the other hand, you see that the measurement device is in a particular state—having measured a spin-up electron. The wave function corresponding to that state is a different state than the wave function corresponding to the entangled state. You have a contradiction.
If you want to say that measuring the electron to have spin-up doesn't imply anything about the state of the measurement device, then it seems to me that you've abandoned the whole point of measurement, which is to give information about the world.
It seems clear to me that quantum mechanics in the minimalist interpretation makes an essential distinction between measurements and other interactions. If you take ##H |psirangle = i hbar frac{partial}{partial t} |psirangle## as the equivalent of Newton's laws, then those laws don't describe the two most fundamental empirical facts about quantum mechanics: The fact that measurements result in eigenvalues of the thing being measured, and the the fact that the probabilities are given by the Born rule. Those are new elements that must be introduced into the physics to accommodate measurements.
That's very different from the case of pre-quantum physics. In pre-quantum physics, there are no additional physical laws needed to describe measurement. It is enough to model a measurement device or an observer as a physical system obeying the laws of physics. Then the properties of measurements follow from the rest of the laws of physics.Of course, besides the dynamical laws there are kinematical laws (you have to formulate first). I thought, the quantum postulates of the minimal interpretation are well-known enough, as we have discussed this over and over in the past. Obviously that's not the case. So here are the kinematical postulates again.
(1) A quantum system is defined by an Hilbert space and a realization of an algebra of observables.
(2) Observables are represented by self-adjoint operators, densely defined on Hilbert space (which implies that their (generalized) eigenstates form a complete set). The possible values of the so represented observables are given by the spectrum of these operators.
(3) States are represented by a self-adjoint positive semi definite operator ##hat{rho}##.
(4) The probability for finding an observable ##A## to have the value ##a## in the spectrum of its representing operator ##hat{A}## is given by
$$P(a|hat{rho})=sum_{beta} langle a,beta|hat{rho}|a,beta rangle.$$
Here, ##beta## for each ##a## label the orthonormalized eigenvectors of ##hat{A}## with eigenvalue ##a## (of course ##beta## can also be continuous, but that's only a mathematical detail, unimportant for our discussion).
As in classical physics also in quantum physics measurements are not described by theory but done in the lab. Of course, the measurement devices are constructed based on knowledge about the known laws of physics. How else should you be able to construct them?
What we would then intuitively expect—and perhaps even demand—is that when it’s all said and done, measurement-as-axiom and measurement-as-interaction should turn out to be equivalent, mutually compatible ways of getting to the same final result. But quantum mechanics does not seem to grant us such simple pleasures. Measurement-as-axiom tells us that the post-measurement quantum state of the system will be an eigenstate of the operator corresponding to the measured observable, and that the corresponding eigenvalue represents the outcome of the measurement. Measurement-as-interaction, by contrast, leads to an entangled quantum state for the composite system-plus-apparatus. The system has been sucked into a vortex of entanglement and no longer has its own quantum state. On top of that, the entangled state fails to indicate any particular measurement outcome.That's a problem only if you believe in the necessity of the collapse postulate, which is not necessary at all. It even contradicts fundamental principles (relativistic spacetime structure) and it's almost always not what happens in real experiments. Of course, in some simple cases you can perform von Neumann filter measurements, but this also is within the realm of "measurement-as-interaction" as anything else, as far as quantum theory is considered complete (and today there's nothing known pointing to some incompleteness at all).
In order to make clear that quantum mechanics and Newtonian mechanics aren't comparable in such a simple manner, let me quote Maximilian Schlosshauer/1/ more extensively:
“One way of identifying the root of the problem [the measurement problem] is to point to the apparent dual nature and description of measurement in quantum mechanics. On the one hand, measurement and its effect enter as a fundamental notion through one of the axioms of the theory. On the other hand, there’s nothing explicitly written into these axioms that would prevent us from setting aside the axiomatic notion of measurement and instead proceeding conceptually as we would do in classical physics. That is, we may model measurement as a physical interaction between two systems called “object” and “apparatus”—only that now, in lieu of particles and Newtonian trajectories, we’d be using quantum states and unitary evolution and entanglement-inducing Hamiltonians.
What we would then intuitively expect—and perhaps even demand—is that when it’s all said and done, measurement-as-axiom and measurement-as-interaction should turn out to be equivalent, mutually compatible ways of getting to the same final result. But quantum mechanics does not seem to grant us such simple pleasures. Measurement-as-axiom tells us that the post-measurement quantum state of the system will be an eigenstate of the operator corresponding to the measured observable, and that the corresponding eigenvalue represents the outcome of the measurement. Measurement-as-interaction, by contrast, leads to an entangled quantum state for the composite system-plus-apparatus. The system has been sucked into a vortex of entanglement and no longer has its own quantum state. On top of that, the entangled state fails to indicate any particular measurement outcome.
So we’re not only presented with two apparently mutually inconsistent ways of describing measurement in quantum mechanics, but each species leaves its own bad taste in our mouth.”
/1/ M. Schlosshauer (ed.), Elegance and Enigma, The Quantum Interviews, Springer-Verlag Berlin Heidelberg 2011, pp. 141-142Exactly!
Quantum theory also simply says i∂t|ψ(t)⟩=^H|ψ(t)⟩mathrm{i} partial_t |psi(t) rangle=hat{H} |psi(t) rangle. This is as empty a mathematical phrase as F=maF=ma if you don't tell what it has to do with observables, i.e., measurable quantities.In order to make clear that quantum mechanics and Newtonian mechanics aren't comparable in such a simple manner, let me quote Maximilian Schlosshauer/1/ more extensively:
“One way of identifying the root of the problem [the measurement problem] is to point to the apparent dual nature and description of measurement in quantum mechanics. On the one hand, measurement and its effect enter as a fundamental notion through one of the axioms of the theory. On the other hand, there’s nothing explicitly written into these axioms that would prevent us from setting aside the axiomatic notion of measurement and instead proceeding conceptually as we would do in classical physics. That is, we may model measurement as a physical interaction between two systems called “object” and “apparatus”—only that now, in lieu of particles and Newtonian trajectories, we’d be using quantum states and unitary evolution and entanglement-inducing Hamiltonians.
What we would then intuitively expect—and perhaps even demand—is that when it’s all said and done, measurement-as-axiom and measurement-as-interaction should turn out to be equivalent, mutually compatible ways of getting to the same final result. But quantum mechanics does not seem to grant us such simple pleasures. Measurement-as-axiom tells us that the post-measurement quantum state of the system will be an eigenstate of the operator corresponding to the measured observable, and that the corresponding eigenvalue represents the outcome of the measurement. Measurement-as-interaction, by contrast, leads to an entangled quantum state for the composite system-plus-apparatus. The system has been sucked into a vortex of entanglement and no longer has its own quantum state. On top of that, the entangled state fails to indicate any particular measurement outcome.
So we’re not only presented with two apparently mutually inconsistent ways of describing measurement in quantum mechanics, but each species leaves its own bad taste in our mouth.”
/1/ M. Schlosshauer (ed.), Elegance and Enigma, The Quantum Interviews, Springer-Verlag Berlin Heidelberg 2011, pp. 141-142
It seems clear to me that quantum mechanics in the minimalist interpretation makes an essential distinction between measurements and other interactions. If you take ##H |psirangle = i hbar frac{partial}{partial t} |psirangle## as the equivalent of Newton's laws, then those laws don't describe the two most fundamental empirical facts about quantum mechanics: The fact that measurements result in eigenvalues of the thing being measured, and the the fact that the probabilities are given by the Born rule. Those are new elements that must be introduced into the physics to accommodate measurements.
That's very different from the case of pre-quantum physics. In pre-quantum physics, there are no additional physical laws needed to describe measurement. It is enough to model a measurement device or an observer as a physical system obeying the laws of physics. Then the properties of measurements follow from the rest of the laws of physics.
The only difference is that Newtonian mechanics (and all of classical physics) is deterministic, i.e., the notion of state is different in the sense that knowing the exact state means to know the precise trajectory in phase space (which can be finite-dimensional as for point particle systems in classical mechanics of infinitely-dimensional as in the classical field theories) implies to precisely know the values of all possible observables of the system. In contradistinction to that QT is probabilistic, i.e., knowing the precise state of a system (i.e., being able to prepare it in a pure state) does not imply that all observables take determined values. It's even shown through the Heisenberg-Robertson uncertainty relation that you cannot prepare a state in which all observables take determined values, but that's the only difference.The only difference between ice cream and sand is that ice cream is cold and sweet and soft and sand is not. In other words, there is almost no similarity.
The notion of state in the minimalist interpretation of quantum mechanics is that it gives probabilities for measurement results. You can't then turn around and say that a measurement result is just another physical property like any other. No other interaction besides measurements results in probabilistic outcomes.
No, it precisely tells you about the meaning of the symbols used in the formalism. The probabilities according to Born's rule are the physics content of the theory, and as far as I can see the only physics content.So according to the minimal interpretation, there is no physical content to quantum mechanics in the absence of measurements. That's very different from Newtonian physics.
I can just use your sentence with a little change:
In the case of quantum mechanics, you have a description of how objects behave in the absence of any observers or measurements at all. It doesn't become wrong. The formalism precisely tells you how the state evolves with time, given the Hamiltonian of the system. If there's no interaction with a measurement apparatus this describes the system without measuring or observing it.
In Newtonian mechanics you also describe the state of the system without considering measurements as long as you choose not to include the interaction of the system with the measurement apparatus.Except that in your first paragraph, you completely left out probabilities.
They aren't comparable, at all. In the case of Newtonian mechanics, you have a description of how objects behave in the absence of any observers or measurements at all. Then to make the connection with observation/measurement, you only need to make the assumption that your measuring device is a particular system obeying Newton's laws. The fact that a spring scale measures mass follows from the assumptions that (1) the length of a spring is proportional to the force applied, and (2) the force on an object due to gravity is proportional to its mass. Together, these assumptions about a scale as a physical object imply that a scale will measure mass.I can just use your sentence with a little change:
In the case of quantum mechanics, you have a description of how objects behave in the absence of any observers or measurements at all. It doesn't become wrong. The formalism precisely tells you how the state evolves with time, given the Hamiltonian of the system. If there's no interaction with a measurement apparatus this describes the system without measuring or observing it.
In Newtonian mechanics you also describe the state of the system without considering measurements as long as you choose not to include the interaction of the system with the measurement apparatus.
No, it doesn't. It also says to use the Born rule to calculate probabilities when a measurement occurs. There is no such rule in Newtonian mechanics.
I agree that any physical theory has to tell you how to relate the mathematical symbols that appear in the theory to the quantities that are actually measured in experiments. But, again, QM, unlike any other physical theory, does much more than this.No, it precisely tells you about the meaning of the symbols used in the formalism. The probabilities according to Born's rule are the physics content of the theory, and as far as I can see the only physics content. It's probabilistic, and if QT is complete (which I don't know of course, because you can never know, whether any physical theory is complete in the sense that it describes right all of the possible observations of Nature), that's all there is.
The only difference is that Newtonian mechanics (and all of classical physics) is deterministic, i.e., the notion of state is different in the sense that knowing the exact state means to know the precise trajectory in phase space (which can be finite-dimensional as for point particle systems in classical mechanics of infinitely-dimensional as in the classical field theories) implies to precisely know the values of all possible observables of the system. In contradistinction to that QT is probabilistic, i.e., knowing the precise state of a system (i.e., being able to prepare it in a pure state) does not imply that all observables take determined values. It's even shown through the Heisenberg-Robertson uncertainty relation that you cannot prepare a state in which all observables take determined values, but that's the only difference.
As long as there is no deterministic (then necessarily non-local) theory that describes all phenomena, I fear we have to live with the probabilistic description of QT. Nature doesn't ask what we like to have but she is just as she is, and that's what physicists are aiming to figure out through more and more refined observations and mathematical models and theories.
Quantum theory also simply says ##mathrm{i} partial_t |psi(t) rangle=hat{H} |psi(t) rangle##. This is as empty a mathematical phrase as ##F=ma## if you don't tell what it has to do with observables, i.e., measurable quantities.They aren't comparable, at all. In the case of Newtonian mechanics, you have a description of how objects behave in the absence of any observers or measurements at all. Then to make the connection with observation/measurement, you only need to make the assumption that your measuring device is a particular system obeying Newton's laws. The fact that a spring scale measures mass follows from the assumptions that (1) the length of a spring is proportional to the force applied, and (2) the force on an object due to gravity is proportional to its mass. Together, these assumptions about a scale as a physical object imply that a scale will measure mass.
The contrast with the Hamiltonian dynamics of quantum mechanics is enormous.
Yes, you can describe the measurement device as a quantum-mechanical system. You can give it a Hamiltonian and describe how the measurement device interacts with the system being measured. But what that doesn't get you is:
So if you want ##mathrm{i} partial_t |psi(t) rangle=hat{H} |psi(t) rangle## to be the analog of Newton's laws, then it is clear that it doesn't work in the way that Newton's laws do. Without additional assumptions about measurements, you can't get any measurement results from that dynamical equation.
Quantum theory also simply says ##mathrm{i} partial_t |psi(t) rangle=hat{H} |psi(t) rangle##.No, it doesn't. It also says to use the Born rule to calculate probabilities when a measurement occurs. There is no such rule in Newtonian mechanics.
This is as empty a mathematical phrase as ##F=ma## if you don't tell what it has to do with observables, i.e., measurable quantities.I agree that any physical theory has to tell you how to relate the mathematical symbols that appear in the theory to the quantities that are actually measured in experiments. But, again, QM, unlike any other physical theory, does much more than this.
No, I haven't said this. To the contrary I stated that macrscopic properties are emergent and derivable from quantum theory, using the universal physical laws of quantum theory.I don't see how that can possibly be. The issue is that you have to select a basis in order for quantum mechanics to have meaningful probabilities. So in a sense, there are no probabilities at the microscopic level, because microscopically, there is no basis selected. And since the laws of quantum mechanics (in the minimalist interpretation) only describe how probability amplitudes evolve, there would be no such thing as "universal physical laws" at the microscopic level, according to the minimalist interpretation. So there would be no way for macroscopic properties to be emergent from microscopic laws.
I don't really care about the quantum-classical cut, and I haven't mentioned that. But you now agree that the minimal interpretation treats macroscopic interactions differently than microscopic interactions? Surely, one electron scattering off another does not constitute a measurement?No, I haven't said this. To the contrary I stated that macrscopic properties are emergent and derivable from quantum theory, using the universal physical laws of quantum theory.
I think we should end this discussion at this point since obviously we are not able to come to a conclusion anyway, and it's no longer of much use for any of the physics forum's readers.
No, any physical theory has to be able to model measurements. But the mathematical machinery of QM, the thing that makes predictions, does much more than that: it tells you, "when a measurement occurs, use the Born rule to calculate the probabilities of the possible outcomes". No other physical theory has a rule like that embedded in its mathematical machinery. Newton's Laws, to use the example you have been using, don't tell you "when a measurement occurs, use F = ma", for example. They just say "F = ma".Quantum theory also simply says ##mathrm{i} partial_t |psi(t) rangle=hat{H} |psi(t) rangle##. This is as empty a mathematical phrase as ##F=ma## if you don't tell what it has to do with observables, i.e., measurable quantities. The only meaning of force, mass, and acceleration in Newtonian mechanics is through measurement procedures enabling you to measure these quantities. The same holds for state vectors: Together with eigenvectors of self-adjoint operators, representing the observables in the quantum formalism, its physical meaning is through the possibility to measure this observable on an ensemble of equally prepared systems (that's the difference to Newtonian physics indeed: you only make probabilistic statements which need an ensemble to be experimentally tested). The meaning is given by Born's rule, of course: ##P(t,a)=|langle a|psi(t) rangle|^2## is the probability (distribution) to find the value ##a## when measuring the observable ##A##, represented by the self-adjoint operator ##hat{A}## and ##|a rangle## being the eigenvector to the eigenvalue ##a## (assuming for simplicity non-degeneracy of the measured observable).
That's again very easy. Measuring something means to compare the measured quantity with a unit which is defined by a real-world measuring procedure (or more precistely an equivalence class of measurement procedures; e.g., to measure the width of my office I can either use a simple yardstick or nowadays a laser rangefinder, but both measurements define the same quantity "length" of course).
Of course, on my opinion the probabilities of quantum theory do not need any human being to take note about the outcome of the measurement. I thought that's behind your insistence on the claim that QT necessarily implies that the universal physical laws do not hold for measurement devices.
Of coarse, I make this macroscopic-microscopic distinction, but I don't claim that there is a fundamental quantum-classical cut.I don't really care about the quantum-classical cut, and I haven't mentioned that. But you now agree that the minimal interpretation treats macroscopic interactions differently than microscopic interactions? Surely, one electron scattering off another does not constitute a measurement?
@vanhees71, can you at least admit that Newton's laws of motion do not mention measurements? But the axioms of the "minimalist interpretation" do mention measurements?
None of those mention "measurement". I don't see how there is room to argue about that.
I'm asking: What does it mean to measure something? Informally, I measured some property if I performed an action so that afterward, I know its value. That way of phrasing it sounds very solipsistic. Must there be a person around in order for quantum probabilities to be meaningful?
An alternative is to say that system A measures a property of system B if through interacting, the state of system A becomes correlated with that of system B and the alternative values of the property are macroscopically distinguishable. But that way of understanding it makes a macroscopic/microscopic distinction, which you claim not to be making.That's again very easy. Measuring something means to compare the measured quantity with a unit which is defined by a real-world measuring procedure (or more precistely an equivalence class of measurement procedures; e.g., to measure the width of my office I can either use a simple yardstick or nowadays a laser rangefinder, but both measurements define the same quantity "length" of course).
Of course, on my opinion the probabilities of quantum theory do not need any human being to take note about the outcome of the measurement. I thought that's behind your insistence on the claim that QT necessarily implies that the universal physical laws do not hold for measurement devices.
Of coarse, I make this macroscopic-microscopic distinction, but I don't claim that there is a fundamental quantum-classical cut. The classical behavior of macroscopic objects, needed to make a measurement (this is one of the few things I think Bohr in fact got right), is however derivable from standard quantum theory in the minimal interpretation. It's based on using only averaged macroscopic observables of the macroscopic system, which are accurate enough to describe its behavior.
For measurement devices that's not different. Of course it has to interact with the measured object and gets entangled with this object in a way that a macroscopic pointer reading allows to uniquely read off the value of the measured observable.
It is not possible to do physics without measurements, so any physical theory is about measurements.No, any physical theory has to be able to model measurements. But the mathematical machinery of QM, the thing that makes predictions, does much more than that: it tells you, "when a measurement occurs, use the Born rule to calculate the probabilities of the possible outcomes". No other physical theory has a rule like that embedded in its mathematical machinery. Newton's Laws, to use the example you have been using, don't tell you "when a measurement occurs, use F = ma", for example. They just say "F = ma".
Of course are Newton's laws about measurements, because all of physics is about measurements.No, Newton's laws are not about measurements. They are about particles and forces and motion. You can deduce facts about measurements from those laws (under the assumption that your measurement devices themselves are physical systems made up of particles and affected by forces.)
It is not possible to do physics without measurements,That wasn't the question. The question was whether it is possible formulate the minimal interpretation without mentioning measurements. Can you answer that question?
Why should it treat measurements differently?As Maximilian Schlosshauer remarks in “ELEGANCE AND ENIGMA, The Quantum Interviews”:
“Measurement-as-interaction, by contrast [to measurement-as-axiom], leads to an entangled quantum state for the composite system-plus-apparatus. The system has been sucked into a vortex of entanglement and no longer has its own quantum state. On top of that, the entangled state fails to indicate any particular measurement outcome.”
I'm asking a technical question: Is it possible to formulate the minimal interpretation of quantum mechanics in a way that does not mention measurement?It is not possible to do physics without measurements, so any physical theory is about measurements. Your question doesn't make sense to begin with, and that's not philosophy but the simple definition of what physics is about.
The answer seems to be no. That's very different from the case with every other theory of physics.It's not different as with any other thery of physics, because physics is about measurements. Without measurements there's no physics.
Newton's laws are not formulated in terms of measurements. They make predictions about the results of measurements, which is all that you want for a theory to have empirical content.Of course are Newton's laws about measurements, because all of physics is about measurements. You start with the postulates about space and time, which implies that you talk about measurable quantities like the period of a pendulum or a planet orbiting the Sun and about distances and angles of bodies in space. Without at least these kinematical observables you cannot even start to state the postulates!
It shows that you are claiming two contradictory things. If my axioms mention cats, then either the axioms can be reformulated so that cats are not specifically mentioned, or else it's false to claim that they don't treat cats specially. If your axioms mention measurements, then either the axioms can be reformulated so that measurements are not explicitly mentioned, or it's false to claim that they don't treat measurements specially.What you stated is a prediction about the behavior of cats. You use (implicitly) the definition of "cat" and it's a statement about the mechanics of cats, which can be checked by observation. Of course, if you make a statement about something it's a statement about this entity. However, I don't see at all what this has to do with the foundations of quantum theory and particularly what this has to do with the existence of a classical-quantum cut (which you seem to insist on as vehemently as I deny any empirical foundation for its existence) or, for me even on the edge of esoterics, that a piece of matter cannot be described by the universal physical laws of nature only because it's used as a measurement device. Are you really claiming that a piece of wood changes to obey the known physical laws, only because I put some marks of it to use it as a yardstick? For me that would be utter nonsense.
That's simple: By measuring it.I'm asking: What does it mean to measure something? Informally, I measured some property if I performed an action so that afterward, I know its value. That way of phrasing it sounds very solipsistic. Must there be a person around in order for quantum probabilities to be meaningful?
An alternative is to say that system A measures a property of system B if through interacting, the state of system A becomes correlated with that of system B and the alternative values of the property are macroscopically distinguishable. But that way of understanding it makes a macroscopic/microscopic distinction, which you claim not to be making.
there's (a) no difference in the physical laws between situations where a measurement apparatus is used and where this is not the case and (b) that there's no difference between the physical laws concerning many-body systems making up measurement devices and any other quantum system, large or small.But WHERE are the physical laws manifested without a classical context? In the mathematical realm?
Of course, to make a measurement we need a macroscopic device to be able to make a measurement. I've never claimed the contrary.Yes, but I get the impression that you might think this is not a major point, but a practicality?
Without the classical realm, we would not only have problems to make a reliable measurement, we would not have been able to reliable infer the laws of particle physics in the first place from large amounts of measurements! Without this, we could not compute the expectation values because the algorithm is unknown.
I may be taking this a step further here, but i think that the whole notion of physical law becomes fluid once we remove the classical observer. And thus fluidity may be necessary to face, but there is not fluidity in current theory, thanks to relating things to a classical measurement device. Here i think Bohr is very minimalist. He does not assume anything. He just notes that we need the classical context, to construct the questions that define the P-distributions.
The only thing I'm saying is that the classical behavior of macroscopic observables does not contradict the fundamental laws of quantum theory but are well explained by standard (quantum!) statistical physics.A catch is the the laws of standard physics are inferred in the classical realm. You can not first abduce statistical laws, then remove the basis for the statistical processing, and claim that you still have a valid inference. Its a fallacy.
It is one thing to in principle explain a macroscopic piece of metal from QM as a manybody problem, because from the point of view of the human earth based laboratory both are "small". Both are relative to our lab, "small subsystems". But if we make cosmological observations, or scale the classical laboratory down to grain level, this logic breaks.
If we stay away from such extremes, and study only small subsystems – from the point of view of a classical boundary, then current physics works fine. I mainly care about this as i want to develop this. But to develp this its good to first understand the premises of current framework.
/Fredrik
I'm too stupid to understand your demand.I don't think that's true. I think that you are unable to answer because you are holding onto two incompatible beliefs.
Sorry for that. Again: Physics is about observations of nature in a quantitative way, i.e., about measurements.I'm not asking a philosophical question. You have a tendency to turn everything into philosophy, and then state how much you dislike philosophy.
I'm asking a technical question: Is it possible to formulate the minimal interpretation of quantum mechanics in a way that does not mention measurement?
The answer seems to be no. That's very different from the case with every other theory of physics.
Newton's laws are not formulated in terms of measurements. They make predictions about the results of measurements, which is all that you want for a theory to have empirical content.
That's a statement about properties of cats, and of course you can observe it and see, whether it's right or not. That cats very often land on their feet is even an interesting biomechanical issue and well investigated by physicists. I'm only totally unaware what this has to do with the interpretational issues of quantum theory.It shows that you are claiming two contradictory things. If my axioms mention cats, then either the axioms can be reformulated so that cats are not specifically mentioned, or else it's false to claim that they don't treat cats specially. If your axioms mention measurements, then either the axioms can be reformulated so that measurements are not explicitly mentioned, or it's false to claim that they don't treat measurements specially.
What makes something the "measured observable"?That's simple: By measuring it. I think we just are unable to explain to each other what the issue is. Maybe it's better to leave it at that :-(.
Because if you are able to do that, that would demonstrate that the minimalist interpretation does not treat measurement different from other interactions. Nothing short of that would suffice.I'm too stupid to understand your demand. Sorry for that. Again: Physics is about observations of nature in a quantitative way, i.e., about measurements. All I'm saying is that measurement devices and the interactions of measured objects with them are following the universal natural laws discovered by physics, and these rules are quantum. It doesn't make sense to talk about physics at all if you don't talk about observations and measurements, because that's the topic of physics.
Suppose I have a law of physics that states that cats always land on their feet. Does that treat cats differently than other objects? Maybe, maybe not. To prove that it doesn't treat cats specially, you should be able to restate the laws in a way that doesn't mention cats, and the specific claim about cats should be derivable from that. If you can't do that, that means that your laws are treating cats specially.That's a statement about properties of cats, and of course you can observe it and see, whether it's right or not. That cats very often land on their feet is even an interesting biomechanical issue and well investigated by physicists. I'm only totally unaware what this has to do with the interpretational issues of quantum theory.
If you can't restate the minimalist interpretation in a way that doesn't mention measurement (or something equivalent) then to me, that's an indication that it treats measurements differently.Why should it treat measurements differently? Measurements are defined by a measurement apparatus, and the very construction of all measurement apparati I know use the known universal laws of physics. There is not difference whatsoever concerning the applicability of the physical laws to construct a measurement apparatus than any other technical gadget like a car or a smartphone (although particularly the latter also contains a lot of measurement apparati you can even use to do interesting measurements in physics classes).
You keep saying that all theories of physics treat measurement special in the same way, but that's absolutely false. Newtonian physics describes objects and their motion and the forces acting on them. Anything you want to say about measurement follows from Newton's laws plus the assumption that the measurement device is a particular physical system obeying Newton's laws.Sure, and Newtonian physics is as well about quantitative observations and thus measurements in nature. An in principle you are right, Newtonian mechanics also is in principle the sufficient basis to construct all the measurement devices you need to measure the quantities described by Newtonian physics (i.e., times, lengths, and masses; everything else is derived). Of course, the same physical laws are needed and the corresponding theory to define what's measurable (i.e., what are the observables) and at the same time are used to test this very theory. In this sense all experimental tests of physical theories are in fact consistency tests.
Nowadays you need a lot more than just Newtonian mechanics to construct measurement apparati; at least some Faraday and Maxwell electrodynamics is usually applied. Many high-precision measurements use in fact quantum theory. The entire SI units will be redefined soon, making use of the accuracy that can only be achieved by using the properties of quantum theory. E.g., to define the second (which will stay the same as before) you use the stability of atomic transitions (or maybe in the future nuclear transitions, which are even more stable and accurate), only describable by quantum theory. The representation of the ampere will hinge on quantum effects providing accurate quantities described by fundamental constants (among the THE quantum one par excellence, ##hbar##) like the quantization of magnetic moments, Josephson junctions, etc. etc. Classical physics is way to inaccurate to be used to define the base units of the SI for use in the 21st century!
The basis chosen is dicated by the measured observable in the usual way (eigenstates of the corresponding self-adjoint operator representing this observable).What makes something the "measured observable"?
The measurement devices used are just made of ordinary matter and are thus described by standard quantum physics as any other lump of matter. That's all I'm sayingYes, I agree that measurements can be described by quantum mechanics. But that is not sufficient for your claim that there is nothing special about measurements. Measurements in the minimal interpretation also serve as picking out a basis, which is necessary for the interpretation of amplitudes as probabilities. A non-measurement interaction does not pick out a basis.
I think, we go in circles here. It is very clear that physical theories are about describing measurementsNo, they are not. Newton's laws are about objects and forces and motion.
Why should I do that, because I never claimed that this is the goal.Because if you are able to do that, that would demonstrate that the minimalist interpretation does not treat measurement different from other interactions. Nothing short of that would suffice.
Suppose I have a law of physics that states that cats always land on their feet. Does that treat cats differently than other objects? Maybe, maybe not. To prove that it doesn't treat cats specially, you should be able to restate the laws in a way that doesn't mention cats, and the specific claim about cats should be derivable from that. If you can't do that, that means that your laws are treating cats specially.
If you can't restate the minimalist interpretation in a way that doesn't mention measurement (or something equivalent) then to me, that's an indication that it treats measurements differently.
You keep saying that all theories of physics treat measurement special in the same way, but that's absolutely false. Newtonian physics describes objects and their motion and the forces acting on them. Anything you want to say about measurement follows from Newton's laws plus the assumption that the measurement device is a particular physical system obeying Newton's laws.
That's my complaint about what you have said with regard to the minimalist interpretation. They make no sense to me. You have a theory whose assumptions explicitly mention measurement, and then you claim that there is nothing special about measurement. That seems like you're contradicting yourself.
Maybe there is a way to resolve the contradiction, but the minimal interpretation certainly doesn't.I think, we go in circles here. It is very clear that physical theories are about describing measurements, i.e., quantative observations of Nature. What else should physics be about?
The measurement devices used are just made of ordinary matter and are thus described by standard quantum physics as any other lump of matter. That's all I'm saying, and that's how experimentalists construct their measurement devices, i.e., using standard (quantum) physics.
Please state the assumptions of the minimalist interpretation without using the words measurement or macroscopic or observer. Until you can do that, what you're saying makes no sense to me.Why should I do that, because I never claimed that this is the goal. Physics is about measurements and thus to some degree also observers (if you call a computer storage, that saves the outcome of measurements automatically an observer is your choice). The only thing I'm saying is that according to the minimal interpretation there's (a) no difference in the physical laws between situations where a measurement apparatus is used and where this is not the case and (b) that there's no difference between the physical laws concerning many-body systems making up measurement devices and any other quantum system, large or small. Of course, to make a measurement we need a macroscopic device to be able to make a measurement. I've never claimed the contrary. The only thing I'm saying is that the classical behavior of macroscopic observables does not contradict the fundamental laws of quantum theory but are well explained by standard (quantum!) statistical physics.
In the minimalist interpretation, a measurement plays two different roles:
Quantum amplitudes are not probabilities until a basis is chosen. You cannot (or at least, I've never seen it done) make sense of amplitudes as probabilities without picking a basis. It's the second role of a measurement that distinguishes measurements from other interactions.The basis chosen is dicated by the measured observable in the usual way (eigenstates of the corresponding self-adjoint operator representing this observable). That's part of the basic postulates of minimally interpreted QT. At least in statement 1. we start to agree (I hope): There's no difference in interactions between measurement devices and any other piece of matter, which isn't used as a measurement device.
That the contrary is a pretty strange idea becomse also clear as follows: Suppose there's a difference on a fundamental level between a measurement apparatus and just an arbitrary piece of matter, that difference occurs as soon as the apparatus is used to measure something. So I let the measured system interact with the apparatus. At this point it's a "usual interaction" according to your previous claim, as far as I understand. Now I (or my dog or an amoeba?) decides to look at the pointer reading of the device, and all of a sudden the "usual interaction" turns to an "unusual measurement", or how else should I understand the claim? I think this view is due to some Copenhagen flavors, claiming that the mind of an observer is important part of the measurement process. In its extreme form, the Princeton interpretation, only when reading the pointer of the measurement device, the "state collapses", and this collapse is not within the laws of QT. This is precisely what's avoided in the minimal statistical interpretation, not claiming that there's a collapse or any other necessity for "extra rules for measurements".
It's really hard to discuss with people making claims without explaining them sufficiently so that a simple-minded physicist can follow. Now you claim again that the minimal statistical interpretation requires a difference, and again I ask, which difference that might be! I've really no clue, and I'm curious about the answer!Please state the assumptions of the minimalist interpretation without using the words measurement or macroscopic or observer. Until you can do that, what you're saying makes no sense to me.
It's really hard to discuss with people making claims without explaining them sufficiently so that a simple-minded physicist can follow.That's my complaint about what you have said with regard to the minimalist interpretation. They make no sense to me. You have a theory whose assumptions explicitly mention measurement, and then you claim that there is nothing special about measurement. That seems like you're contradicting yourself.
Maybe there is a way to resolve the contradiction, but the minimal interpretation certainly doesn't.
In the minimalist interpretation, a measurement plays two different roles:
Quantum amplitudes are not probabilities until a basis is chosen. You cannot (or at least, I've never seen it done) make sense of amplitudes as probabilities without picking a basis. It's the second role of a measurement that distinguishes measurements from other interactions.
It's really hard to discuss with people making claims without explaining them sufficiently so that a simple-minded physicist can follow. Now you claim again that the minimal statistical interpretation requires a difference, and again I ask, which difference that might be! I've really no clue, and I'm curious about the answer!
Again you simply make bold claims without explanation.I'm not making a claim—I'm pointing out that what you are claiming is just not true. The minimalist interpretation makes a distinction between a measurement and other kinds of interactions. It's right there in the definition of how the wave function is interpreted. I'm not making a claim about quantum mechanics; it's certainly possible that there could be an interpretation that doesn't make such a distinction (maybe Many-Worlds, or maybe Bohmian). But that isn't the minimalist interpretation.
To make my still unanswered question very simple: What's the (principle) difference between the interaction of a photon hitting a CCD screen (measurement device) and just some other plane like my desk? I don't see, where there should be a differenceI agree. There shouldn't be a difference. But the minimalist interpretation requires a difference. So the minimalist interpretation is unsatisfactory for that reason. It's fine as a rule of thumb, but it can't be literally true.
Again you simply make bold claims without explanation. To make my still unanswered question very simple: What's the (principle) difference between the interaction of a photon hitting a CCD screen (measurement device) and just some other plane like my desk? I don't see, where there should be a difference. It's all the good old electromagnetic interaction, isn't it? Of course, if you think photons to be too special (and they are special), just take any massive particle you like to explain clearly in physical terms the difference between interacting of the particle with a measurement device and just matter that isn't used as a measurement device.
To be honest, I think it's ridiculous to think that there are different laws for this interaction simply because once the material is used as a measurement apparatus and the other time it's not. The very design of any physical measurement device (starting from something as simple as a yardstick up to the most complicated high-accuracy devices used for high-precision measurements in (sub-)atomic physics) are based on the fundamental laws of physics, which are believed to hold true universally and do not have exception only because something is used as a measurement device. There's even no different physical law for things living or non-living. There's no "vis viva" but just the fundamental interactions of physics at work also in living organisms. This is just another example for claims in the past that physical laws might not be universal. It's one of the great achievements of science to find universal laws. Although being far from trivial to exist, all quantitative and qualitative experience shows this universality.
This seems pretty straightforward: If there is no distinction between measurement-like interactions and non-measurement interactions, then it should be possible to formulate the minimalist interpretation in which the word "measurement" is replaced by its definition—something like "an interaction between two systems such that a property of one system causes a macroscopic change in the other system". If you try to do that, you will see that the minimalist interpretation inherently involves a microscopic/macroscopic distinction.
I am not! If you read the physics content of all standard textbooks, all there is predicted are probabilities for the outcome of measurements, and these predictions are in excellent agreement with all experiments done so far. That's the core of quantum theory, and that's the physics described by it. It's called the minimal statistical interpretation, and it's within the Copenhagen class of interpretation, taken away the unnecessary problematic parts, i.e., the collapse (in contradiction with relativistic space-time structure and causality) and a quantum-classical cut, which nobody has ever been able to demonstrate experimentally. To the contrary, the more advanced (quantum) engineering gets, the larger systems can be prepared in states that behave "quantum like" not "classical like", although the common "classical-like states" of everyday matter around us is of course also a quantum state. Classical physics is a limit for classical behavior of macroscopic properties which are coarse-grained quantities that averaged over many microscopic degrees of freedom. The rest is the math of the central-limit theorem of standard probability theory.I'm not disagreeing with the claim that quantum mechanics makes good predictions, I'm just saying that it is patently wrong to say that it makes those predictions without distinguishing measurements from non-measurements.
Bringing up the central limit theorem is just not relevant to this question. It's a non-sequitur. It's possible (in principle, if not in practice) to treat a measurement interaction quantum-mechanically, but when you do so, the probabilities disappear. To recover probabilities, you need yet another system that is not treated quantum-mechanically that will measure the measuring device. There are no probabilities associated with a pure quantum-mechanical system. At least not in the minimal interpretation. That's why I say that bringing up the central limit theorem is a non-sequitur. The central limit theorem is concerned with probabilities, and the issue is whether there are any probabilities at all involved in a quantum system where you treat everything (including observers and measurement devices) quantum-mechanically. Invoking the central limit theorem is assuming your conclusion.
I don't see why this is even controversial. The basic assumptions of the "minimalist interpretation" only say what happens when a measurement is performed. That's very different from the assumptions of Newtonian mechanics, which say what happens when massive particles interact through forces. Whether or not anything is measured it doesn't make any difference.
I am not! If you read the physics content of all standard textbooks, all there is predicted are probabilities for the outcome of measurements, and these predictions are in excellent agreement with all experiments done so far. That's the core of quantum theory, and that's the physics described by it. It's called the minimal statistical interpretation, and it's within the Copenhagen class of interpretation, taken away the unnecessary problematic parts, i.e., the collapse (in contradiction with relativistic space-time structure and causality) and a quantum-classical cut, which nobody has ever been able to demonstrate experimentally. To the contrary, the more advanced (quantum) engineering gets, the larger systems can be prepared in states that behave "quantum like" not "classical like", although the common "classical-like states" of everyday matter around us is of course also a quantum state. Classical physics is a limit for classical behavior of macroscopic properties which are coarse-grained quantities that averaged over many microscopic degrees of freedom. The rest is the math of the central-limit theorem of standard probability theory.
Why aren't there situations where quantum states are naturally falling into eigenstates of some operator – without measurement – for instance on a star?
This could happen trillions of times and thus a probability distribution. Or is any time a quantum states projects onto an eigen state of an operator a measurement by definition?This is not standard quantum mechanics. This is what is proposed in attempts to solve the measurement problem such as the physical collapse theories like GRW. Although vanhees71 is an expert on quantum field theory, in these fundamental and basic points, he is in contradiction to almost all standard textbooks of quantum physics.
There is no distinction between measurements and other interactions.In the way i am sure you mean it i fully agree.
But the distinction is in its description; and the description (and the expectations) are encoded in the observer part. The "questions asked" about an subatomic system, are in a deep way "formulated" and encoded physically in the observing system. The computational inference machinery required, for constructing questions (ie. observations) live in the observer part of the cut in my view.
If we relax this (which takes us beyond the standard theory) things become very complicated. Its to avoid this we need the "classical reference". Of course my opinon is that at some point we need to face these problems, but that is exactly the questions we need to ask to go beyond QM as it stands, to understand QG and unification imo.
/Fredrik
The "wave function" is a probability amplitude by definition (within the standard minimal interpretation). Thus it's probabilistic from the very beginning, without any necessity to introduce classical concepts.A probability distribution itself is classical statistical concept, involving no uncertainties. At this level quantum mechanics is just a deterministic theory as is newtons mechanics.
The laws of quantum theory deductively infers distribution of events, given a preparation. So the heart of the predictions is at the level of distributions.
Its just the link to single outcomes that is probabilistic. But this link, depends on a definite distribution; which IMO is anchored in the observer part of the system. And the reason this is considered to be in the realm of classical mechanics is that intercommunication within the measurment device is considered trivial in comparasion. One effectively assumes that (if we forget about relativity for a second) that all classical observers are equivalent, and thus we attain objectivity. But this objectivity (observer equivalent) only is manifested in the classical realm.
Ie. without a classical context for the measuremnt device, you can not defined a definite distribution, and not even a certain probability. Then even the probability gets "undertain", in an uncontrollable way.
/Fredrik
I sketched this in another post a while back.
[..]
So the Born rule in my understanding requires a distinction between macroscopic coarse-grained descriptions (where the rule applies) and microscopic descriptions (where it does not).Thanks ! I think Sewell and some of the refs therein have something about this. I will reply ( if this thread is dead I'll start a new one).
Can you expand that ? It might help to understand what the 'split' actually is.I sketched this in another post a while back.
But let's suppose that coarse-graining can be mathematically defined in terms of projection operators. Let ##|psirangle## be the state of the complete system (environment plus measuring devices plus observers plus …). Then we want a set of projection operators ##Pi_j## such that:
Then the Born rule can be formulated as: The probability of the system being in coarse-grained state ##j## is given by:
##P(j) = langle psi|Pi_j|psi rangle##
So the Born rule applies to coarse-grained projection operators.
The usual Born rule can be derived from this one. The usual formulation says that if you measure a property of a subsystem, then you will get an eigenvalue, with probabilities given by the square of the amplitude corresponding to the decomposition of the subsystem state into eigenstates. But if you interpret "measurement" as meaning: "A process whereby the value of the microscopic quantity is amplified to make a macroscopic difference", then different values of the microscopic property will lead to different coarse-grained states of the measurement device.So the Born rule on coarse-grained states implies that you will get results with the right probabilities.
But note: To have agreement with observation, you only need the Born rule to apply to coarse-grained projections, not to arbitrary (microscopic) projections. And furthermore, I don't know of a way to consistently extend the Born rule in terms of projections to microscopic properties. I don't think there is any way.
So the Born rule in my understanding requires a distinction between macroscopic coarse-grained descriptions (where the rule applies) and microscopic descriptions (where it does not).
by naturally I just meant without measurement.But under what circumstances would a star or whatever naturally make a transition into an eigenstate of some operator?
No, coarse-graining doesn't explain anything. It's another way of formulating the split.Can you expand that ? It might help to understand what the 'split' actually is.
I wasn't giving my opinion about it—I was describing the orthodox interpretation of quantum mechanics, which is that the probabilities in quantum mechanics are probabilities of measurement results.
An alternative interpretation which I think is empirically equivalent is to forget about measurements, and instead think of QM as a stochastic theory for macroscopic configurations. What I think is nice about this approach is that it doesn't single out measurements, and it doesn't require the assumption that a measurement always gives an eigenvalue of the operator corresponding to the observable being measured. It doesn't require observers, so you can apply QM to situations like distant stars where there are no observations. On the other hand, it's got the same flaw as the orthodox interpretation, in that it requires a macroscopic/microscopic distinction.
Getting back to your specific comment, I'm not sure what you mean by "naturally falling into eigenstates". Could you elaborate?by naturally I just meant without measurement.
Ok, if you think so, I've to accept it, but then how can you explain the classical behavior of macroscopic objects from quantum theory at all, or are you really thinking, there's a cut on a fundamental level? If so, where's the empirical evidence for it?I'm saying that the minimalist interpretation of quantum mechanics makes a distinction between measurement interactions and other interactions. I'm not saying that it is impossible to come up with an interpretation of quantum mechanics that doesn't rely on such a split, only that your preferred interpretation requires it.
Let's suppose that we have a device that measures the spin of an electron along the z-axis as follows:
If you treat the pointer like a quantum-mechanical object, then you would have to conclude:
But the Born rule says something different:
That rule is unlike anything you would say about microscopic systems.
Of course, Newtonian physics is about measurements.No, it is not. Certainly not in the sense that QM is about measurements. Newtonian physics is about the motion of particles under the influence of forces. The connection with measurement requires an assumption that the forces and/or particle motions have an affect on the measuring device. So what Newtonian physics says about measurement is derivable from Newtonian physics (possibly with other assumptions). It is not cooked into Newtonian physics.
If you assume that a spring deforms in a linear way when a force is applied to one end, then the spring can be used for measurement of forces. But it would be a mistake to define force in terms of the deformation of springs.
No, coarse-graining doesn't explain anything. It's another way of formulating the split.Ok, if you think so, I've to accept it, but then how can you explain the classical behavior of macroscopic objects from quantum theory at all, or are you really thinking, there's a cut on a fundamental level? If so, where's the empirical evidence for it?
. That is not the truth. Newtonian physics is not formulated in terms of measurements. Neither is any other theory of physics besides the minimal interpretation..All theories are written to express the outcomes of measurements ( or observations). It is not stated explicitly because it is obvious. J J Gleason identifies any formula that gives the value of a classical outcome as an operator, in anaolgy with QT.
Of course, Newtonian physics is about measurements. To write down a position vector you already need to define it in terms of measurable quantities, e.g., the three Cartesian coordinates with respect to an appropriate reference frame (provided, e.g., by three rigid rods of unit length put together at a point or the edges in one corner of your lab, etc.). Physics is about measurable quantities.
Again you only stated that the minimal interpretation depends on a distinction between measurement and other interactions, but you did not tell WHAT difference this might be and why this distinction is even NECESSARY.
Sure, but the classical describability of macroscopic properties is not due to some cut, beyond which quantum theory isn't valid anymore, but it's explanable by coarse graining from quantum many-body systems.No, coarse-graining doesn't explain anything. It's another way of formulating the split.
Sigh. It is really difficult to make this simple argument. Of course, I have to mention measurments. I have to state it, because physics is about measurements. What else should it be about?That is not the truth. Newtonian physics is not formulated in terms of measurements. Neither is any other theory of physics besides the minimal interpretation. What you're saying is just not true. You're interpreting things through your personal philosophy.
What all theories of physics must have (if they are supposed to be fundamental) is a correspondence between observations and phenomena described in the theory. If you have a theory of light, then for it to have observational content, you need something along the lines of the assumption that seeing involves light entering our eyes and registering with sensors there. But the theory of light is not expressed in terms of observations. Maxwell's equations do not mention observations. Newton's laws don't mention observations. General Relativity doesn't mention observations. You don't need for a theory to be about measurements in order to have empirical content, you need to be able to describe how the phenomena described by the theory affects what is observable.
That's the point, not to avoid the word "measurement" or "observation". Again, where is, in your opinion, the necessity to invoke classical arguments here? You havent's defined, what you mean by "classically observe".I didn't mention the word "classical" either. I said that the probabilistic predictions of QM (at least in the minimal interpretation—things are different in the Bohmian interpretation and the consistent histories interpretation and the many-worlds interpretation) depend on a distinction between "measurement" and other interactions.
One attempt might be the following: We say that system ##A## (the measuring device) measures a property of a second system, ##B## if the interaction between the two systems causes an irreversible change in the state of system ##A## such that distinct values of the property of system ##B## reliably lead to macroscopically distinguishable states of system ##A##. This definition of "measurement" seems to necessarily involve distinguish macroscopic properties from microscopic properties.Sure, but the classical describability of macroscopic properties is not due to some cut, beyond which quantum theory isn't valid anymore, but it's explanable by coarse graining from quantum many-body systems.
I'm saying that the minimal interpretation already has that split. Try formulating the probabilistic predictions of the minimalist interpretation without mentioning "measurement".Sigh. It is really difficult to make this simple argument. Of course, I have to mention measurments. I have to state it, because physics is about measurements. What else should it be about? I never have to use the word "classical" in all these definitions. That's the point, not to avoid the word "measurement" or "observation". Again, where is, in your opinion, the necessity to invoke classical arguments here? You havent's defined, what you mean by "classically observe".
Let's take a photon. It's observed by letting it interact with a detector (in former days a photo plate, nowadays some electronic detector like a CCD). There's not the slightest hint that the interaction of the photon with the photo plate or CCD cam is any different from the electromagnetic interactions described by QED.
I'm saying that the minimal interpretation already has that split. Try formulating the probabilistic predictions of the minimalist interpretation without mentioning "measurement".If you want to treat a measurement as just another interaction, then you should be able to formulate the probabilistic predictions of quantum mechanics without mentioning the word "measurement".
One attempt might be the following: We say that system ##A## (the measuring device) measures a property of a second system, ##B## if the interaction between the two systems causes an irreversible change in the state of system ##A## such that distinct values of the property of system ##B## reliably lead to macroscopically distinguishable states of system ##A##. This definition of "measurement" seems to necessarily involve distinguish macroscopic properties from microscopic properties.
Of course, there are alternative interpretations, but the minimal interpretation seems to me to absolutely require such a distinction. You cannot make sense of the minimalist interpretation without this distinction (or something equivalent: macroscopic versus microscopic, irreversible versus reversible, measurement versus non-measurement).
I don't have a proof that it is impossible to make sense of Born probabilities without making such a distinction, I'm just claiming that the minimalist interpretation does not do so.