Why the Quantum | A Response to Wheeler’s 1986 Paper
Wheeler’s opening statement in his 1986 paper, “How Come the Quantum?” holds as true today as it did then [1]
The necessity of the quantum in the construction of existence: out of what deeper requirement does it arise? Behind it all is surely an idea so simple, so beautiful, so compelling that when — in a decade, a century, or a millennium — we grasp it, we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?
In this Insight, I will answer Wheeler’s question per its counterpart in quantum information theory (QIT), “How come the Tsirelson bound?” Let me start by explaining the Tsirelson bound and its relationship to the Bell inequality, then it will be obvious what that has to do with Wheeler’s question, “How Come the Quantum?” The answer (the Tsirelson bound is a consequence of conservation per no preferred reference frame (NPRF)) may surprise you with its apparent simplicity, but that simplicity belies a profound mystery, as we will see.
The Tsirelson bound is the spread in the Clauser-Horne-Shimony-Holt (CHSH) quantity
\begin{equation}\langle a,b \rangle + \langle a,b^\prime \rangle + \langle a^\prime,b \rangle – \langle a^\prime,b^\prime \rangle \label{CHSH1}\end{equation}
created by quantum correlations. Here, we consider a pair of entangled particles (or “quantum systems” or “quantum exchanges of momentum”). Alice makes measurements on one of the two particles with her measuring device set to ##a## or ##a^\prime## while Bob makes measurements on the other of the two particles with his measuring device set to ##b## or ##b^\prime##. There are two possible outcomes for either Bob or Alice in either of their two possible settings given by ##i## and ##j##. For measurements at ##a## and ##b## we have for the average of Alice’s results multiplied by Bob’s results on a trial-by-trial basis
\begin{equation}\langle a,b \rangle = \sum (i \cdot j) \cdot P(i,j \mid a,b) \label{average}\end{equation}
That’s a bit vague, so let me supply some actual physics. The two entangled states I will use are those which uniquely give rise to the Tsirelson bound [2-4] , i.e., the spin singlet state and the ‘Mermin photon state’ [5]. The spin singlet state is ##\frac{1}{\sqrt{2}} \left(\mid ud \rangle – \mid du \rangle \right)## where ##u##/##d## means the outcome is displaced upwards/downwards relative to the north-south pole alignment of the Stern-Gerlach (SG) magnets (Figure 1).
 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
This state obtains due to conservation of angular momentum at the source as represented by momentum exchange in the spatial plane P orthogonal to the source collimation (“up or down” transverse). This state might be produced by the dissociation of a spin-zero diatomic molecule [6] or the decay of a neutral pi meson into an electron-positron pair [7], processes which conserve spin angular momentum. For more information about the spin singlet state and the spin triplet states, see this Insight.
The Mermin state for photons is ##\frac{1}{\sqrt{2}} \left(\mid VV \rangle + \mid HH \rangle \right)## where ##V## means the there is an outcome (photon detection) behind one of the coaligned polarizers and ##H## means there is no outcome behind one of the co-aligned polarizers. This state obtains due to conservation of angular momentum at the source as represented by momentum exchange along the source collimation (“yes” or “no” longitudinal). Dehlinger and Mitchell created this state by laser inducing spontaneous parametric downconversion in beta barium borate crystals [8], a process that conserves spin angular momentum as represented by the polarization of the emitted photons. At this point we will focus the discussion on the spin single state for total anti-correlation, since everything said of that state can be easily transferred to the Mermin photon state.
Let us investigate what Alice and Bob discover about these entangled states in the various contexts of their measurements (Figure 2). Alice’s detector responds up and down with equal frequency regardless of the orientation ##\alpha## of her SG magnet. This is in agreement with the relativity principle, aka “no preferred reference frame” (NPRF), where different SG magnet orientations relative to the source constitute different “reference frames” in quantum mechanics just as different velocities relative to the source constitute different “reference frames” in special relativity (see this Insight).
Figure 2. Alice and Bob making spin measurements in the xz plane on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors.
Bob observes the same regarding his SG magnet orientation ##\beta##. Thus, the source is rotationally invariant in the spatial plane P orthogonal to the source collimation. When Bob and Alice compare their outcomes, they find that their outcomes are perfectly anti-correlated (##ud## and ##du## with equal frequency) when ##\alpha – \beta = \theta = 0## (Figure 3). This is consistent with conservation of angular momentum per classical mechanics between the pair of detection events (again, this fact defines the state). The degree of that anti-correlation diminishes as ##\theta \rightarrow \frac{\pi}{2}## until it is equal to the degree of correlation (##uu## and ##dd##) when their SG magnets are at right angles to each other. In other words, whenever the SG magnets are orthogonal to each other anti-correlated and correlated outcomes occur with equal frequency, i.e., conservation of angular momentum in one direction is independent of the angular momentum changes in any orthogonal direction. Thus, we wouldn’t expect to see more correlation or more anti-correlation based on conservation of angular momentum for transverse results in the plane P when the SG magnets are orthogonal to each other. As we continue to increase the angle ##\theta## beyond ##\frac{\pi}{2}## the anti-correlations continue to diminish until we have totally correlated outcomes when the SG magnets are anti-aligned. This is also consistent with conservation of angular momentum, since the totally correlated results when the SG magnets are anti-aligned represent momentum exchanges in opposite directions in the plane P just as when the SG magnets are aligned, it is now simply the case that what Alice calls up, Bob calls down and vice-versa.
The counterpart for the Mermin photon state is simply that angular momentum conservation is evidenced by ##VV## or ##HH## outcomes for coaligned polarizers. When the polarizers are at right angles you have only ##VH## and ##HV## outcomes, which is still totally consistent with conservation of angular momentum as ‘not ##H##’ implies ##V## and vice-versa [8]. In other words, a polarizer does not have a ‘north-south’ distinction (longitudinal rather than transverse momentum exchange). In particular, having rotated either or both polarizers by ##\pi## one should obtain precisely ##VV## or ##HH## outcomes again.
Nothing is particularly mysterious about the entangled states for electron spin or photon polarization described here so far because we have been thinking as if conservation of angular momentum holds for each experimental trial, as in classical mechanics. Truth is, since Alice and Bob can only measure +1 or -1 (quantum exchange of momentum per NPRF), we can only get conservation of angular momentum in any particular trial when their SG magnets/polarizers are co-aligned. And, we cannot use classical probability theory to account for the conservation of angular momentum on average.
In particular, the probability that Alice and Bob will measure ##uu## or ##dd## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityuu}\end{equation}
And, the probability that Alice and Bob will measure ##ud## or ##du## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityud}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##u##) and -1 (##d##) gives Eq. (\ref{CHSH1}) of
\begin{equation}-\cos(a – b) -\cos(a – b^\prime) -\cos(a^\prime – b) +\cos(a^\prime – b^\prime) \label{CHSHspin}\end{equation}
Choosing ##a = \pi/4##, ##a^\prime = -\pi/4##, ##b = 0##, and ##b^\prime = \pi/2## minimizes Eq. (\ref{CHSHspin}) at ##-2\sqrt{2}## (the Tsirelson bound).
Likewise, for the Mermin photon state we have
\begin{equation}P_{VV} = P_{HH} = \frac{1}{2} \mbox{cos}^2 \left(\alpha – \beta \right) \label{probabilityVV}\end{equation}
and
\begin{equation}P_{VH} = P_{HV} = \frac{1}{2} \mbox{sin}^2 \left(\alpha – \beta \right) \label{probabilityVH}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##V##) and -1 (##H##) gives Eq. (\ref{CHSH1}) of
\begin{equation}\cos2(a – b) +\cos2(a – b^\prime) +\cos2(a^\prime – b) -\cos2(a^\prime – b^\prime) \label{CHSHmermin}\end{equation}
Using ##a = \pi/8##, ##a^\prime = -\pi/8##, ##b = 0##, and ##b^\prime = \pi/4## maximizes Eq. (\ref{CHSHmermin}) at ##2\sqrt{2}## (the Tsirelson bound). So, we have two mysteries.
First, as explained by Mermin [5], suppose you restrict Alice and Bob’s measurement angles ##\alpha## and ##\beta## to three possibilities, setting 1 is ##0^o##, setting two is ##120^o##, and setting three is ##-120^o##. Eq. (\ref{probabilityud}) says the probability of getting opposite results is 1 when ##\alpha = \beta## (1/2 ##ud## and 1/2 ##du##) and 1/4 otherwise (1/8 ##ud## and 1/8 ##du##). Now, if the source emits particles with definite properties that account for their outcomes in the three possible measurement settings, and we have to get total anti-correlation for like settings, then the particles’ so-called “instruction sets” must be opposite for each of the three settings. For example, suppose we have 1(##u##)2(##u##)3(##d##) for Alice and 1(##d##)2(##d##)3(##u##) for Bob. That guarantees the total anti-correlation for like settings, i.e., 11 gives ##ud##, 22 gives ##ud##, and 33 gives ##du##. And, for unlike settings we get anti-correlation in two combinations, i.e., 12 gives ##ud## and 21 gives ##ud##. In fact, for any instruction set with two ##u## and one ##d## we get anti-correlation for unlike settings in two of the six possible unlike combinations (12,13,21,23,31,32). The only other way to make a pair of instruction sets is to have one with all ##u## and the other with all ##d##. In that case, we get anti-correlation for all six unlike combinations. That means the instruction sets necessary to guarantee anti-correlation for like settings lead to an overall anti-correlation greater than 2/6 for unlike settings, which is greater than the quantum probability for anti-correlation in unlike settings of 1/4. This is Mermin’s version of the Bell inequality [9] (fraction of anti-correlated outcomes for unlike settings must be greater than 2/6) and the manner by which it is violated by quantum correlations (1/4 is less than 2/6). Thus, instruction sets (“counterfactual definiteness”) assumed by classical probability theory cannot account for quantum correlations in this case.
The counterpart to this for the CHSH quantity is that classical correlations give a range of -2 to 2 for the CHSH quantity (“CHSH-Bell inequality”). And, as we saw above, the Tsirelson bound violates the CHSH-Bell inequality. Experiments show that the quantum results can be achieved (violating the Bell inequality), ruling out an explanation of these correlated momentum exchanges via instruction sets per classical probability theory.
The second mystery is that even in cases where we don’t violate the Bell inequality, e.g., ##a = b = 0## and ##a^\prime = b^\prime = \pi/2## which give a CHSH value of 0, we still have conservation of angular momentum. Why is that mysterious? Well, it’s not when the SG magnets are co-aligned, since in those cases we always get a +1 outcome and a -1 outcome for a total of zero. But, in trials where ##\alpha – \beta = \theta## does not equal zero, we need either Alice or Bob, at minimum, to measure something less than 1 to conserve angular momentum. For example, if Alice measures +1, then Bob must measure ##-\cos{\theta}## to conserve angular momentum for that trial. But, again, Alice and Bob only measure +1 or -1 (quantum exchange of momentum per NPRF, which uniquely distinguishes the quantum joint distribution from its classical counterpart [10]), so that can’t happen (Figure 4). What does happen? We conserve angular momentum on average in those trials.
It is easy to see how this follows by starting with total angular momentum of zero for binary (quantum) outcomes +1 and -1 (I am suppressing the factor of ##\hbar/2## and I’m referring to the spin singlet state here [11], Figure 3).

Figure 3. Outcomes (yellow dots) in the same reference frame, i.e., outcomes for the same measurement (blue arrows represent SG magnet orientations), for the spin singlet state explicitly conserve angular momentum.
Alice and Bob both measure +1 and -1 results with equal frequency for any SG magnet angle (NPRF) and when their angles are equal they obtain different outcomes giving total angular momentum of zero. The case (a) result is not difficult to understand via conservation of angular momentum, because Alice and Bob’s measured values of spin angular momentum cancel directly when ##\alpha = \beta##, that defines the spin singlet state. But, when Bob’s SG magnet is rotated by ##\alpha – \beta = \theta## relative to Alice’s, the situation is not as clear (Figure 6).
In classical physics, one would say the projection of the angular momentum vector of Alice’s particle ##\vec{S}_A = +1\hat{a}## along ##\hat{b}## is ##\vec{S}_A\cdot\hat{b} = +\cos{(\theta)}## where again ##\theta## is the angle between the unit vectors ##\hat{a}## and ##\hat{b}## (Figure 2). From Alice’s perspective, had Bob measured at the same angle, i.e., ##\beta = \alpha##, he would have found the angular momentum vector of his particle was ##\vec{S}_B = -1\hat{a}##, so that ##\vec{S}_A + \vec{S}_B = \vec{S}_{Total} = 0##. Since he did not measure the angular momentum of his particle at the same angle, he should have obtained a fraction of the length of ##\vec{S}_B##, i.e., ##\vec{S}_B\cdot\hat{b} = -1\hat{a}\cdot\hat{b} = -\cos{(\theta)}## (Figure 4).

Figure 4. The projection of the angular momentum of Bob’s particle ##\vec{S}_B## along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum due to NPRF.
Of course, Bob only ever obtains +1 or -1 per NPRF, so Bob’s outcomes can only average the required ##-\cos{(\theta)}##. Thus, NPRF dictates
\begin{align*}
P_{uu} + P_{ud} & = \frac {1}{2} \\
P_{ud} + P_{dd} & = \frac {1}{2},
\end{align*}
These equations now allow us to uniquely solve for the joint probabilities
\begin{equation}
P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\theta}{2} \right) \label{QMjointLike}
\end{equation}
and
\begin{equation}
P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\theta}{2} \right) \label{QMjointUnlike}
\end{equation}
\begin{equation}
\overline{BA-} = 2P_{du}(+1) + 2P_{dd}(-1) = \cos (\theta) \label{BA-}
\end{equation}
Using Eqs. (\ref{BA+}) and (\ref{BA-}) in Eq. (\ref{consCorrel}) we obtain
\begin{equation}
\langle \alpha,\beta \rangle = \frac{1}{2}(+1)_A(-\mbox{cos} \left(\theta\right)) + \frac{1}{2}(-1)_A(\mbox{cos} \left(\theta\right)) = -\mbox{cos} \left(\theta\right) \label{consCorrel2}
\end{equation}
which is precisely the correlation function for a spin singlet state found using the joint probabilities per quantum mechanics. To see that we simply use Eqs. (\ref{probabilityuu}) and (\ref{probabilityud}) in Eq. (\ref{average}) to get
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)(-1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(+1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) +\\ &(+1)(+1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(-1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \\ &= -\mbox{cos} \left(\alpha – \beta \right) = -\mbox{cos} \left(\theta \right)
\end{split}
\label{correl}\end{equation}
Thus, “average-only” conservation maps beautifully to our classical expectation (Figures 6 & 7). Since the angle between SG magnets ##\theta## is twice the angle between Hilbert space measurement bases, this result easily generalizes to conservation per NPRF of whatever the measurement outcomes represent when unlike outcomes entail conservation in the symmetry plane [15] (see this Insight on the Bell spin states). However, again, none of the formalism of quantum mechanics is used in obtaining Eq. (\ref{consCorrel2}) or our quantum state Eqs. (\ref{QMjointLike}) & (\ref{QMjointUnlike}). In deriving the quantum correlation function and quantum state in this fashion, we assumed only NPRF.For the Mermin photon state, conservation of angular momentum is established by ##V## (designated by +1) and ##H## (designated by -1) results through a polarizer. When the polarizers are co-aligned Alice and Bob get the same results, half pass and half no pass. Thus, conservation of angular momentum is established by the intensity of the electromagnetic radiation applied to binary outcomes for various polarizer orientations. As with spin angular momentum, this is classical thinking applied to binary outcomes per conservation of angular momentum. Again, grouping Alice’s results into +1 and -1 outcomes we see that she would expect to find ##[\mbox{cos}^2\theta – \mbox{sin}^2\theta]## at ##\theta## for her +1 results and ##[\mbox{sin}^2\theta – \mbox{cos}^2\theta]## for her -1 results. Since Bob measures the same thing as Alice for conservation of angular momentum, those are Bob’s averages when his polarizer deviates from Alice’s by ##\theta##. Therefore, the correlation of results for conservation of angular momentum is given by
\begin{equation}\langle \alpha,\beta \rangle =\frac{(+1_A)(\mbox{cos}^2\theta – \mbox{sin}^2\theta)}{2} + \frac{(-1_A)(\mbox{sin}^2\theta – \mbox{cos}^2\theta)}{2} = \cos{2\theta} \label{merminconserve}\end{equation}
which is precisely the correlation given by quantum mechanics.As before, we need to find ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## so we need four independent conditions. Normalization and ##P_{VH} = P_{HV}## are the same as for the spin case. The correlation function
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)_A(+1)_BP_{VV} + (+1)_A(-1)_BP_{VH} + \\&(-1)_A(+1)_BP_{HV} + (-1)_A(-1)_BP_{HH}\label{correlFn2}
\end{split}
\end{equation}
along with our conservation principle represented by Eq. (\ref{merminconserve}) give
\begin{equation}
P_{VV} – P_{VH} = -\frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
and
\begin{equation}
P_{HV} – P_{HH} = \frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
Solving these four equations for ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## gives precisely Eqs. (\ref{probabilityVV}) & (\ref{probabilityVH}).Notice that since the angle between polarizers ##\alpha – \beta## equals the angle between Hilbert space measurement bases, this result immediately generalizes to conservation per NPRF of whatever the outcomes represent when like outcomes entail conservation in the symmetry plane [15] (again, see this Insight on the Bell spin states).Since the quantum correlations violate the Bell inequality to the Tsirelson bound and satisfy conservation per NPRF while the classical correlations do not violate the Bell inequality, the classical correlations do not satisfy conservation per NPRF. Experiments of course tell us that Nature obeys the quantum correlations and therefore the conservation per NPRF.

Figure 5. A spatiotemporal ensemble of 8 experimental trials for the Bell spin states showing Bob’s outcomes corresponding to Alice‘s ##+1## outcomes when ##\theta = 60^\circ##. Angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{60^\circ}=\frac{1}{2}##). It is impossible for angular momentum to be conserved explicitly in each trial since the measurement outcomes are binary (quantum) with values of ##+1## (up) or ##-1## (down) per no preferred reference frame. The conservation principle at work here assumes Alice and Bob’s measured values of angular momentum are not mere components of some hidden angular momentum with variable magnitude. That is, the measured values of angular momentum are the angular momenta contributing to this conservation.
Figure 6. For the spin singlet state (S = 0). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from –1 (totally down, arrow bottom) to 0 to +1 (totally up, arrow tip). This obtains per conservation of angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of angular momentum on average, because they only measure +1/-1, never a fractional result. Thus, just as with the light postulate of special relativity, we see that no preferred reference frame leads to counterintuitive results (see this Insight).
Figure 7. The situation is similar for the spin triplet states where outcomes agree for the same measurement in the plane containing the conserved angular momentum vector (S = 1). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to –1 (totally down, arrow bottom). This obtains per conservation of angular momentum on average in the plane containing the S = 1 spin angular momentum in accord with no preferred reference frame. See this Insight for details.
So, while conservation per NPRF sounds like a very reasonable constraint on the distribution of quantum exchange of momentum (+1 or -1, no fractions), we still do not have any causal mechanism to explain the outcomes of any particular trial when the SG magnets/polarizers are not co-aligned (Figure 4). And, as I showed above, we cannot use instruction sets per classical probability theory to account for the Tsirelson bound needed to explain the conservation of angular momentum on average. Thus, while we have a very reasonable constraint on the distribution of entangled quantum exchanges (conservation of angular momentum), that constraint has no compelling dynamical counterpart, i.e., no consensus causal mechanism to explain the outcome of any particular trial when the SG magnets/polarizers are not co-aligned and no counterfactual definiteness to explain why conservation of angular momentum is conserved on average. What we have is a “principle” account of entanglement and the Tsirelson bound (see this Insight). I will return to this point after showing how so-called “superquantum correlations” fail to satisfy this constraint as well.
There are QIT correlations that not only violate the Bell inequality, but also violate the Tsirelson bound. Since these correlations violate the Tsirelson bound, they are called “superquantum correlations.” The reason QIT considers these correlations reasonable (no known reason to reject their possibility) is because they do not violate superluminal communication, i.e., the joint probabilities don’t violate the no-signaling condition
\begin{equation}\begin{split}P(A \mid a\phantom{\prime},b\phantom{\prime}) &= P(A \mid a\phantom{\prime}, b^\prime)\\
P(A \mid a^\prime,b\phantom{\prime}) &= P(A \mid a^\prime, b^\prime)\\
P(B \mid a\phantom{\prime},b\phantom{\prime}) &= P(B \mid a^\prime, b\phantom{\prime})\\
P(B \mid a\phantom{\prime},b^\prime) &= P(B \mid a^\prime, b^\prime )\end{split}\label{nosig}\end{equation}
This means Alice and Bob measure the same outcomes regardless of each other’s settings. If this wasn’t true, Alice and Bob would notice changes in the pattern of their outcomes as the other changed their measurement settings. Since the measurements for each trial can be spacelike separated that would entail superluminal communication.
The Popescu-Rohrlich (PR) joint probabilities
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
produce a value of 4 for Eq. (\ref{CHSH1}), the largest of any no-signaling possibilities. Thus, the QIT counterpart to Wheeler’s question, “How Come the Quantum?” is “Why the Tsirelson bound?” [12-14]. In other words, is there any compelling principle that rules out superquantum correlations as conservation of angular momentum ruled out classical correlations? Let us look at Eq. (\ref{PRcorr}) in the context of our spin singlet and Mermin photon states. Again, we will focus the discussion on the spin singlet state and allude to the obvious manner by which the analysis carries over to the Mermin photon state.
The last PR joint probability certainly makes sense if ##a^\prime = b^\prime##, i.e., the total anti-correlation implying conservation of angular momentum, so let us start there. The third PR joint probability makes sense for ##b = \pi + b^\prime##, where we have conservation of angular momentum with Bob having flipped his coordinate directions. Likewise, then, the second PR joint probability makes sense for ##a = \pi + a^\prime##, where we have conservation of angular momentum with Alice having flipped her coordinate directions. All of this is perfectly self consistent with conservation of angular momentum as we described above, since ##a^\prime## and ##b^\prime## are arbitrary per rotational invariance in the plane P. But now, the first PR joint probability is totally at odds with conservation of angular momentum. Both Alice and Bob simply flip their coordinate directions, so we should be right back to the fourth PR joint probability with ##a^\prime \rightarrow a## and ##b^\prime \rightarrow b##. Instead, the first PR joint probability says that we have total correlation (maximal violation of conservation of angular momentum) rather than total anti-correlation per conservation of angular momentum, which violates every other observation. In other words, the set of PR observations violates conservation of angular momentum in a maximal sense. To obtain the corresponding argument for angular momentum conservation per the correlated outcomes of the Mermin photon state, simply start with the first PR joint probability and show the last PR joint probability maximally violates angular momentum conservation.
To find the degree to which superquantum correlations violate our constraint, replace the first PR joint probability with
\begin{equation}\begin{split}&p(1,1 \mid a,b) = C \\
&p(-1,-1 \mid a, b) = D \\
&p(1,-1 \mid a,b) = E \\
&p(-1,1 \mid a, b) = F \\ \end{split} \label{PRcorrMod}\end{equation}
The no-signaling condition Eq. (\ref{nosig}) in conjunction with the second and third PR joint probabilities gives ##C = D## and ##E = F##. That in conjunction with normalization ##C + D + E + F =1## and P(anti-correlation) + P(correlation) = 1 means total anti-correlation (##E = F = 1/2##, ##C = D = 0##) is the conservation of angular momentum per the quantum case while total correlation (##E = F = 0##, ##C = D = 1/2##) is the max violation of conservation of angular momentum per the PR case. To get the corresponding result for the Mermin photon state, simply replace the last PR joint probability in analogous fashion, again with ##\theta = \pi##. In that case, the PR joint probabilities violate conservation of angular momentum with total anti-correlation while the Mermin photon state satisfies conservation of angular momentum with total correlation. Thus, we have a spectrum of superquantum correlations all violating conservation of angular momentum.
So, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a ‘causal influence’ or hidden variables acting on a trial-by-trial basis to account for that conservation. That is the essence of a “principle theory.” Indeed, the kinematic structure (Minkowski spacetime) of special relativity and the kinematic structure (qubit Hilbert space) of quantum mechanics both follow from NPRF, so we now know that quantum mechanics is on par with special relativity as a principle theory (again, see this Insight).
Therefore, my answer to QIT’s version of Wheeler’s question is
The Tsirelson bound obtains because of conservation per no preferred reference frame.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation per NPRF [16,17,18]) to dispel the mystery of entanglement and answer Wheeler’s question depends on whether or not you can accept the fundamentality of a principle explanation via patterns in both space and time (see this Insight). While we have a compelling 4D constraint (who would argue with conservation per NPRF?) for our adynamical explanation, we do not have a compelling dynamical counterpart. That is, we do not have a consensus, causal mechanism to explain outcomes on a trial-by-trial basis when the SG magnets/polarizers are not co-aligned, and we cannot use counterfactual definiteness per classical probability theory to account for the fact that we conserve angular momentum on average. So, perhaps we do not need new physics to rise to Wilczek’s challenge [19].
To me, ascending from the ant’s-eye view to the God’s-eye view of physical reality is the most profound challenge for fundamental physics in the next 100 years.
[Note: “God’s-eye view” simply means the blockworld, block universe, “all-at-once”, or 4D view like that of Minkowski spacetime, there is no religious connotation.] Since special relativity already supports that view, perhaps we should accept that adynamical explanation is fundamental to dynamical explanation, so that not all adynamical explanations have dynamical counterparts [20]. In that case, “we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?” [1]
References
- Wheeler, J.A.: How Come the Quantum?, New Techniques and Ideas in Quantum Measurement Theory 480(1), 304–316 (1986).
- Cirel’son, B.S.: Quantum Generalizations of Bell’s Inequality, Letters in Mathematical Physics 4, 93–100 (1980).
- Landau, L.J.: On the violation of Bell’s inequality in quantum theory, Physics Letters A 120(2), 54–56 (1987).
- Khalfin, L.A., and Tsirelson, B.S.: Quantum/Classical Correspondence in the Light of Bell’s Inequalities, Foundations of Physics 22(7), 879–948 (1992).
- Mermin, N.D.: Bringing home the atomic world: Quantum mysteries for anybody, American Journal of Physics 49(10), 940–943 (1981).
- Bohm, D.: Quantum Theory, Prentice-Hall, New Jersey (1952).
- La Rosa, A.: Introduction to Quantum Mechanics, Chapter 12
- Dehlinger, D., and Mitchell, M.W.: Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory, American Journal of Physics 70(9), 903–910 (2002).
- Bell, J.: On the Einstein-Podolsky-Rosen paradox, Physics 1, 195–200 (1964).
- Garg, A., and Mermin, N.D.: Bell Inequalities with a Range of Violation that Does Not Diminish as the Spin Becomes Arbitrarily Large, Physical Review Letters 49(13), 901–904 (1982).
- Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
- Bub, J.: Bananaworld: Quantum Mechanics for Primates, Oxford University Press, Oxford, UK (2016).
- Bub, J.: Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B, 241–266 (2004).
- Bub, J.: Why the Tsirelson bound?, in The Probable and the Improbable: The Meaning and Role of Probability in Physics, eds. Meir Hemmo and Yemima Ben-Menahem, Springer, Dordrecht, 167–185 (2012).
- Weinberg, S.: The Trouble with Quantum Mechanics (2017).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Kohler, I: Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum, Entropy 21(7), 692 (2019).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D.: Answering Mermin’s challenge with conservation per no preferred reference frame, Scientific Reports 10, 15771 (2020).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s, Entropy 23(1), 114 (2021).
- Wilczek, F.: Physics in 100 Years, Physics Today 69(4), 32–39 (2016).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford University Press, Oxford, UK (2018).
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018).


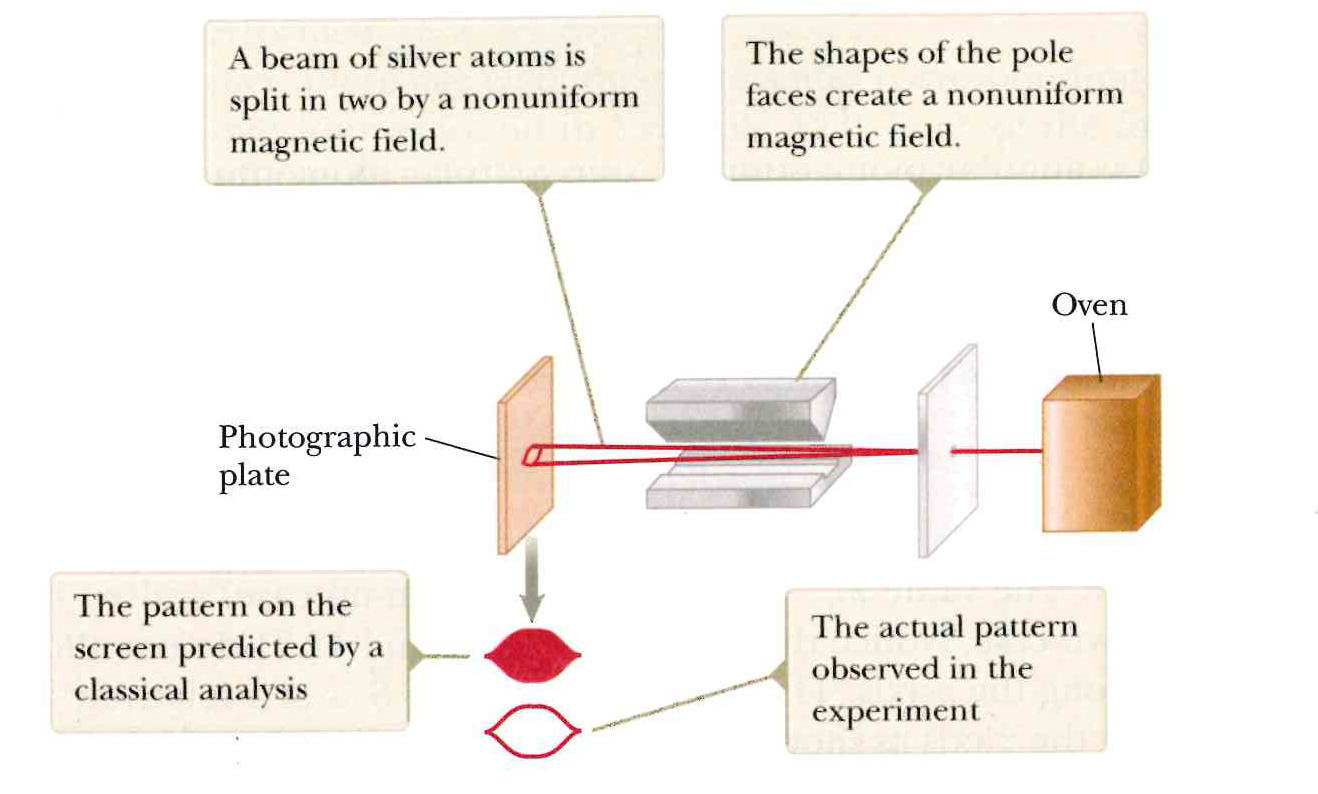 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.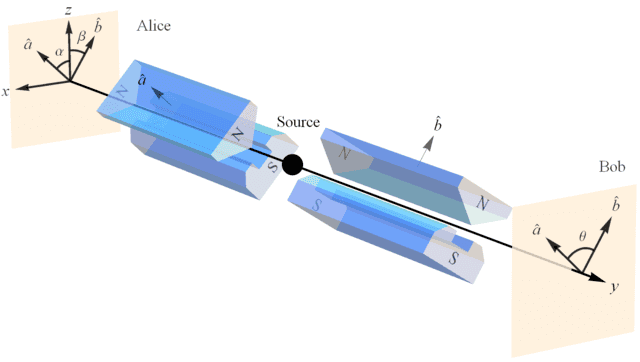








The difference only is that in classical mechanics it's postulated that all observables always have a determined value and of course that means that if you measure these observables you observe these determined values, while QT tells us that not all observables can take determined values, no matter in which state the system may be prepared, and thus the only sensible meaning of the quantum state are the probabilities given by Born's Rule.Consider a classical stochastic process, e.g. a random walk. The observables are not deterministic, but given by a probabilistic law. Yet, observables have definite values at each time, irrespective of whether you measure them or not. I think the key to understand QM is to explain what exactly is the difference between QM and classical stochastic processes.
I meant the theory cannot make any predictions without a cut. If the observer is included in the wave function and all we have is the unitarily evolving quantum state, the theory makes no predictions.So is the cut necessary to predict that electric charge will be conserved?
I meant the theory cannot make any predictions without a cut. If the observer is included in the wave function and all we have is the unitarily evolving quantum state, the theory makes no predictions.I agree. And to include the observer, we need ANOTHER observer. And then what we get are the predictions of this OTHER observers measurements on the composite system.
But if we repeat this, we realize that at some point the predictions are ONLY at the infinite boundary of the composite system. Which is the same situation as saying that all we can predict are the S-matrix, we can not make predictions of the interior, we can only predict the interactions at the observer boundary. All this is fine for lab work, but becomes completely meaningless for cosmological theories. This is for me the real motivation for this discussion IMO.
/Fredrik
I don't think that's true. Newton's laws have the same physical content even in the absence of human beings and measuring devices.I think a scientific theory can never be detached from its historical inference; because the explanation lies in its history. You can certainly do that mathematically, but then you loose contact to the experiment, and it even misses out the important theoretical aspect and meaning of interactions and evolution of the theory.Even newtons laws are indeed inferred from actual interactions (measurements)! In this sense there is actually not much fo a difference.
The difference is that in classical mechanics we can afford to "trivialize" measurements in a way, that makes us think they arent part of interactions. But I think this is a deep mistake.
The typical rebuttal to this argument is that i am here confusing the laws of nature with the human knowledge of them (and human theories) but its not that simple unfortunately. There is a much deeper meaning of this.
/Fredrik
Keep in mind I’m not a “research physicist,” I just teach physics at a 4-year college. Therefore, I’m just trying to figure out a way to make sense of the physics we already have. The interpretation I’m presenting allows me to do that without instrumentalism, i.e., I’m providing a model of physical reality as Becker argued. It took me 24 years and now that I have it I must admit per Wheeler, “how could I have been so stupid for so long?” It’s actually pretty simple once you see it. But, I understand research physicists have a different agenda, so I don’t want to rain on your parade :-)
But I thought you retain the classical-quantum cut?Quantum-classical contextuality means there is a classical context for every quantum exchange of momentum. However, there is no “cut” as regards size. As Gerry et al. showed, you can reach the Tsirelson bound with large angular momentum if properly screened off. In other words, you’ll get an elephant interference pattern if you screen off elephants in the twin-slit experiment (as already done with 60-atom molecules). QM states don’t care about the size of the objects involved.
Maximal violations of a Bell inequality by entangled spin-coherent states
author = {Gerry, Christopher C. and Benmoussa, Adil and Hach, Edwin E. and Albert, Jaroslav},
journal = {Phys. Rev. A},
volume = {79},
issue = {2},
pages = {022111},
numpages = {4},
year = {2009},
month = {Feb},
publisher = {American Physical Society},
doi = {10.1103/PhysRevA.79.022111},
note = {url{https://link.aps.org/doi/10.1103/PhysRevA.79.022111}}
No, no, our interpretation totally solves the MP and keeps QM intact. The MP obtains because physicists want a model of physical reality that is dynamical and reductive, but Nature is under no obligation to be the way we want it to be.To me, the measurement problem should really be called the probability problem. The equations of quantum mechanics describe probability amplitudes. To get a probability out of that, you have to pick a basis (or a projection operator or more generally, a positive-operator valued measure). Picking a basis or an operator is roughly speaking what the "cut" is about.
No, no, our interpretation totally solves the MP and keeps QM intact. The MP obtains because physicists want a model of physical reality that is dynamical and reductive, but Nature is under no obligation to be the way we want it to be.But I thought you retain the classical-quantum cut?
Okay. My remark is about the non-exceptional probabilities, that are neither 0 nor 1, but somewhere in between. I guess I would agree that if QM predicts that the probability amplitude for something is 0 or 1, then you don't need to know anything more than that.One always needs a cut, even for probabilities of 0 or 1. If the observer is included in the wave function, there are no measurement outcomes and no probabilities, which come only when the Born rule is applied.
I guess your interpretation is not an "interpretation" in traditional quantum terminology since it retains the cut and doesn't attempt to solve the measurement problem.
Especially since you frame it with Wheeler's question, which was not about solving the measurement problem, I guess your programme is more like trying to provide alternative axioms for quantum theory, like the odl quantum logic thinking of von Neumann, Birkhoff, Mackey, etc, and the more recent ones of Lucien Hardy https://arxiv.org/abs/quant-ph/0101012 or of Chiribella and colleagues https://arxiv.org/abs/1011.6451 ?No, no, our interpretation totally solves the MP and keeps QM intact. The MP obtains because physicists want a model of physical reality that is dynamical and reductive, but Nature is under no obligation to be the way we want it to be.
How exactly in these examples? A photon will not decay to a proton. What detection is needed to make such a prediction? Just for the prediction, not to actually test it. Or black holes radiate, where is the detection here? I am not saying that it isn't there, it is just not obvious to me.Okay. My remark is about the non-exceptional probabilities, that are neither 0 nor 1, but somewhere in between. I guess I would agree that if QM predicts that the probability amplitude for something is 0 or 1, then you don't need to know anything more than that.
Quantum mechanics gives the amplitudes for particle interactions. To actually get probabilities out of them, you have to assume that somewhere down the road, someone is going to be detecting those particles.How exactly in these examples? A photon will not decay to a proton. What detection is needed to make such a prediction? Just for the prediction, not to actually test it. Or black holes radiate, where is the detection here? I am not saying that it isn't there, it is just not obvious to me.
I thought that QT can make predictions without any cut. Say, if you smash these particles, then the probability to get those is so and so. No cut and a very spesific prediction. Or something along the lines a black hole will radiate and loose energy, no cut. Or is the cut somewhere implicit.Quantum mechanics gives the amplitudes for particle interactions. To actually get probabilities out of them, you have to assume that somewhere down the road, someone is going to be detecting those particles.
There is no physical content of any theory without measurementsI don't think that's true. Newton's laws have the same physical content even in the absence of human beings and measuring devices.
if not you cant compare it to experiment so its not testable ie its not science.I agree with that. Science is about how we go about finding out what is true about the world—developing theories and testing them, etc. But that doesn't mean that the physical content of the theory is about measurements.
The issue with QM is defining, using nothing but QM itself, what a measurement its.I don't think that is the issue. A measurement device can be said to measure a physical property of a system being measured if the interaction between measuring device and system leads to a macroscopic difference in the device such that different values of the physical property lead to persistent, observable differences in the state of the device. Or something like that. That is not the issue for quantum mechanics.
People sometimes talk about things like "the irreversible interaction between the system and an environment" as a kind of measurement. But it certainly isn't. Not in the sense of the rhetoric that "science is about measurement".
The issue for quantum mechanics is understanding how probabilities arise and how alternative possibilities become real.
It has long been my 'feeling' that some issues in QM people worry about are also present in other theories like probability and classical mechanics, however they are generally not worried about in those areas – except maybe by philosophers.In classical physics, probability is not fundamental but a result of trying to deal with imperfect information. So it's very different from quantum mechanics in that respect.
I guess your interpretation is not an "interpretation" in traditional quantum terminology since it retains the cut and doesn't attempt to solve the measurement problem.
Especially since you frame it with Wheeler's question, which was not about solving the measurement problem, I guess your programme is more like trying to provide alternative axioms for quantum theory, like the odl quantum logic thinking of von Neumann, Birkhoff, Mackey, etc, and the more recent ones of Lucien Hardy https://arxiv.org/abs/quant-ph/0101012 or of Chiribella and colleagues https://arxiv.org/abs/1011.6451 ?Well, I think there is no measurement problem for the simple reason that QT works extraordinary well to describe what's observed in Nature and measured with high precision in the lab.
Wow, it always amazes me how many human-IQ-hours have been invested trying to find a way to reinvent QM so as to rid it of the measurement problem (see Schlosshauer quote in #135). Accepting QM as supplying spatiotemporal constraints on the distribution of quantum events, rather than dynamical laws for the behavior of quantum systems, automatically rids us of the MP. Then, QM is seen as complete by simply accepting quantum-classical contextuality. There is nothing in Nature that demands we recover classical reality from a quantum reality in toto. Certainly not with any empirical consequences. That's just a reductive bias. If Weinberg tried and failed, it's certainly above my pay grade! But, it looks to be entertaining lots of brilliant mathematical minds, so by all means, enjoy :-)I couldn't agree more!
Newton's equation is a statement of the form "position of the particle is such and such". It is not a statement of the form "When position of the particle is measured, then position of the particle is such and such".
But quantum mechanics is different. QM does not state that "probability of the position of the particle is such and such". It states that "When position of the particle is measured, then probability of the position of the particle is such and such".The statement of QT is indeed not "When position of the particle is measured, then position of the particle is such and such" but "When the position of the particle is measured the probability distribution for the outcome of this measurement is given by Born's rule". Within QT there's nothing else known about the position than these probabilities. It seems as if we agree in fact about this. The difference only is that in classical mechanics it's postulated that all observables always have a determined value and of course that means that if you measure these observables you observe these determined values, while QT tells us that not all observables can take determined values, no matter in which state the system may be prepared, and thus the only sensible meaning of the quantum state are the probabilities given by Born's Rule.
But how is it you don't buy your own preferred interpretation ?
But first things first, I don't (nor anybody else) think (let's say on a philosophical/ontological level) that the "stuff" of the laboratory (or the universe or whatnot) is made of two different "categories" of stuff, obeying different rule. For example I am quite confident that classical mechanics assume you can measure things of the theory (like force and mass and …) with the same thing in the laboratory (force and mass) (in the same unit)
Also the discussion here is only about phenomenology, and differences between them (and their completeness)
Maybe in the lab… but you seem to be doubting that… I don't. And again, it is not the "problem". The problem is to accurately analyse the theory itself.Then please precisely explain to me what you mean when you say "measurements are special" (within quantum mechanics). I have no clue what that should mean if you admit that measurement devices are usual "stuff" and thus behaves according to the generally valid physical laws. Indeed, measuring a force with a balance invokes the very laws the concept of force is based on within the theory (necessarily Newtonian mechanics, because the force concept only makes sense within Newtonian mechanics). I'm not doubting that, but you do, if I understand the statement "measurements are special". I'm arguing against this claim of the Copenhagen-like interpretation all the time.
All of physics is about phenomenogy. Theory aims at ever more comprehensive and ever more precise description of phenomena that are objectively observable in Nature. This does not imply a positivistic view on physical theories. QT is the prime example that the formalism is in very abstract terms which are not directly observable. QT is rather a mathematical formalism to predict probabilities for the outcome of measurements, and these probabilities are observables on ensembles via statistical evaluation methods.
What is uncontroversial, in that in the model/theory the physical law describe imaginary(hmmm complex) vector in arbitrary dimension. From what I understand the Schrodinger equation is deterministic and continuous.
Where I think you make a unconscious philosophical leap, is to believe that measurement apparatus (used to test QM) are "displaying" those imaginary pointer from other dimensions… they don't. Not because they are macroscopic, but because the unit don't even match those of the theory…
…because the complete minimal interpretation must add something fundamentally different to classical mechanic, in order to make it scientific (testable).
This process (the Born rule) is discrete, and only happens "on measurement" (not on interaction), and is probabilistic. But at least probabilities of "stuff" in the same unit as the laboratory (all classical).That's exactly what I meant above: The wave function, which is a way to describe the quantum state for a special case, i.e., for systems of a fixed set of stable particles that can be described non-relativisticall, is not directly observable, but with the Hamiltonian of the it provides position or momentum probablity distributions (depending on whether you work in the position or momentum representation, but you can always convert from one to the other) given an initial condition. This time evolution is, for a closed system, described by a unitary time-evolution operator, and of coarse QT is causal (and even in a narrower sense causal, because it's also local in time, i.e., you need to know the initial condition just at one initial time, not the entire history of the wave function in the past). QT is, however, not deterministic (within the minimal interpretation and most other interpretations too). One has to distinguish between causality (knowing the state in the past tells you precisely the state in the future) and determinism (all observables of a system always have determined values, no matter in which state this system is in). Again: QT is causal but not deterministic.
Ok, then my mistake. When do you use the Born rule inside the Schrodinger equation ?
That's an ontological claim (that I share btw).
But you don't claim that. You are claiming (as far as I understand) that the epistemology is not based on such a dichotomy.What do you mean by that? I don't use Born's rule inside the Schrödinger equation. For me Born's rule is an independent postulate, necessary to give an interpretation to the wave function (in this very special case of systems, where a wave function is a sufficient description of the (pure) quantum states of the system) usable in the lab. The wave function and the Schrödinger equation is just a means to calculate these probabilities. There's no (direct) ontic meaning of the states (in the general case represented statistical operators) and obserables (represented by essentially self-adjoint operators). These are only tools to calculate the probabilities, which can be observed (on ensembles of equally prepared systems).
But there is no need to. The minimalist interpretation is fine. You believe in ensemble, and the Born rule applied. Period.Exactly. So far there's nothing else.
You seem to believe that one day another interpretation will derive the Born Rule. Why not ? As far I can tel RUTA's one is a good start. It is even based on a classical axiom…Well, it might well be that one day we'll find another more comprehensive theory, where QT turns out to be an effective theory with the Born rule derived from the more comprehensive theory. It's, maybe, even likely, when we understand quantum gravity better than we do now. So far the Born rule seems to be an independent postulate, necessary to give a minimal interpretation needed to apply the QT formalism to real-world observations.
But as thing are currently, the current minimal interpretation does make such a distinction.Which "distinction"?
No, the units don't match in QM, they do in CM
As far as I known, probabilities are not complex numbers… even (0,0)I have no clue, what you want to tell by this statements. The same units are used in QT as in classical physics. Already now many units are based on QT, because that's much more precise than using the historical original definitions based on classical physics. It is almost certain that the entire SI will be based on QT already next year, 2019.
Probabilities are of course numbers between 0 and 1. I've no clue, why you think probabilities might be complex numbers.
Of course when speaking about probabilities you have different views on that – Vanhees and myself take the Frequentest view – as many people in areas that apply probability do – but it is far from the only one. The frequentest view naturally leads to the Ensemble interpretation. As John Baez says much of the argument about QM interpretations is the same as arguments about what probability means:
http://math.ucr.edu/home/baez/bayes.html
Me and Vanhees do not ascribe to the Bayesian view – but really its just philosophy and in applying it makes no difference in practice – well most of the time anyway.
Thanks
BillBhobbas perspective (especially on symmetry) has been quite different than mine in past discussions on here, but I fully agree here that the above is indeed at the heart of the discussions! So we probably agree roughly where the core of the issues are but not on the resolution.
QM foundations is certainly (in one way or the other) about connecting the foundations of inference using probability, statistics or what framework you prefer – to the foundations of physics and measurement and science.
My own perspective is that of inference with a mix between frequentist and bayesian, as i argue that the process of actually counting and computing (in the frequentist view) is subjective (hence the bayesian angle). This is because i conjecture that the process of arriving at the expectations from "counting, datareducing and storing" data from history is a physical process, that are encoded in the microstructure of matter. But this perspective also makes it clear what current formulation of QM need relaxation and revisiion. But its equally clear to me at least why – until then – the original Bohr view of the classical measurement device is required for formulating quantum theory in a physically meaningful way (not talking about math realm where you can of course have not constraint on your fantasies)
/Fredrik
Because in classical mechanics the particle is there whether you look at it or not. In quantum mechanics, the formalism does not assign the particle a position until you look at it.
In quantum mechanics, there is a fundamental difficulty with applying the quantum state to the whole universe including the observer. In classical mechanics, there is no equivalent difficulty (there is a difficulty to include the whole universe from the singularities of GR, but that is different from needing to exclude the observer).In quantum mechanics a particle is there too, provided there's a conservation law ensuring this. If there is no conservation law there's a certain probability that the particle vanishes by interaction with other particles. The only difference is that the position of a particle is never determined, and thus in any state the probability distribution has a finite width around a point (if you consider a state where the particle is pretty well localized) or it might even be a very broad distribution or the distribution might peak around different locations (if the particle is not so well localized).
As I already wrote yesterday, indeed the notion of the "quantum state of the entire universe" doesn't make sense within the minimal interpretation. However "the entire universe" is a pretty abstract and unapproachable fiction. If you believe in inflation, and there are good reasons to believe in the cosmological standard model with inflation (whatever the "mechanism" behind it might be), then it's clear that "the entire universe" isn't even in principle observable. In this sense we always deal with open systems.
Wow, it always amazes me how many human-IQ-hours have been invested trying to find a way to reinvent QM so as to rid it of the measurement problem (see Schlosshauer quote in #135). Accepting QM as supplying spatiotemporal constraints on the distribution of quantum events, rather than dynamical laws for the behavior of quantum systems, automatically rids us of the MP. Then, QM is seen as complete by simply accepting quantum-classical contextuality. There is nothing in Nature that demands we recover classical reality from a quantum reality in toto. Certainly not with any empirical consequences. That's just a reductive bias. If Weinberg tried and failed, it's certainly above my pay grade! But, it looks to be entertaining lots of brilliant mathematical minds, so by all means, enjoy :-)I guess your interpretation is not an "interpretation" in traditional quantum terminology since it retains the cut and doesn't attempt to solve the measurement problem.
Especially since you frame it with Wheeler's question, which was not about solving the measurement problem, I guess your programme is more like trying to provide alternative axioms for quantum theory, like the odl quantum logic thinking of von Neumann, Birkhoff, Mackey, etc, and the more recent ones of Lucien Hardy https://arxiv.org/abs/quant-ph/0101012 or of Chiribella and colleagues https://arxiv.org/abs/1011.6451 ?
I meant the theory cannot make any predictions without a cutWhat about my examples?
Wow, it always amazes me how many human-IQ-hours have been invested trying to find a way to reinvent QM so as to rid it of the measurement problem (see Schlosshauer quote in #135). Accepting QM as supplying spatiotemporal constraints on the distribution of quantum events, rather than dynamical laws for the behavior of quantum systems, automatically rids us of the MP. Then, QM is seen as complete by simply accepting quantum-classical contextuality. There is nothing in Nature that demands we recover classical reality from a quantum reality in toto. Certainly not with any empirical consequences. That's just a reductive bias. If Weinberg tried and failed, it's certainly above my pay grade! But, it looks to be entertaining lots of brilliant mathematical minds, so by all means, enjoy :-)
Again for me this is the very statement, I don't buy. There is no difference between interaction and measurement. This is vaguely formulated, so maybe I understand you and other proponents of this claim in this thread in a wrong way. For me this says that you and others claim that there's a difference in the interaction of the measured object with the measurement apparatus and all other interactions.But how is it you don't buy your own preferred interpretation ?
But first things first, I don't (nor anybody else) think (let's say on a philosophical/ontological level) that the "stuff" of the laboratory (or the universe or whatnot) is made of two different "categories" of stuff, obeying different rule. For example I am quite confident that classical mechanics assume you can measure things of the theory (like force and mass and …) with the same thing in the laboratory (force and mass) (in the same unit)
Also the discussion here is only about phenomenology, and differences between them (and their completeness)
This doesn't make sense to me since the same physical laws apply to interactions no matter whether it's the interaction with a measurement apparatus or not.Maybe in the lab… but you seem to be doubting that… I don't. And again, it is not the "problem". The problem is to accurately analyse the theory itself.
What is uncontroversial, in that in the model/theory the physical law describe imaginary(hmmm complex) vector in arbitrary dimension. From what I understand the Schrodinger equation is deterministic and continuous.
Where I think you make a unconscious philosophical leap, is to believe that measurement apparatus (used to test QM) are "displaying" those imaginary pointer from other dimensions… they don't. Not because they are macroscopic, but because the unit don't even match those of the theory…
…because the complete minimal interpretation must add something fundamentally different to classical mechanic, in order to make it scientific (testable).
This process (the Born rule) is discrete, and only happens "on measurement" (not on interaction), and is probabilistic. But at least probabilities of "stuff" in the same unit as the laboratory (all classical).
Neither in classical nor in quantum theory is any dichotomy in the applicability of the rules to measurement apparati and other objects.Ok, then my mistake. When do you use the Born rule inside the Schrodinger equation ?
Measurement apparati are made of the same stuff as anything else, and also all physical laws apply to measurement devices as to any other object. That's all I'm claiming.That's an ontological claim (that I share btw).
But you don't claim that. You are claiming (as far as I understand) that the epistemology is not based on such a dichotomy.
Maybe we have to reformulate our claims, but I don't know, in which way I can reformulate mine.But there is no need to. The minimalist interpretation is fine. You believe in ensemble, and the Born rule applied. Period.
You seem to believe that one day another interpretation will derive the Born Rule. Why not ? As far I can tel RUTA's one is a good start. It is even based on a classical axiom…
But as thing are currently, the current minimal interpretation does make such a distinction.
Both phase space in classical mechanics and the operators in Hilbert space are representing properties of observable facts about objects, described in an abstract mathematical way.No, the units don't match in QM, they do in CM
In QT the description is explicitly probabilisticAs far as I known, probabilities are not complex numbers… even (0,0)
Because in classical mechanics the particle is there whether you look at it or not. In quantum mechanics, the formalism does not assign the particle a position until you look at it.Even after measurement you still don't have a value – only a (hopefully) more precise probability !
Only projective measurements allow one to say what the state is. And in that case it is not a measurement because all information about the original state has been lost.
That statement, taken literally, was wrong. But it's clear (at least to me) that atyy wanted to say that the theory cannot make some of its predictions without a cut.I would have said: the theory cannot make verifiable prediction without a cut.
Is there some theoretical predictions that could lead to 0 or 1 without a the need of some previous measurement (based on known eigenvalue ?).
That statement, taken literally, was wrong. But it's clear (at least to me) that atyy wanted to say that the theory cannot make some of its predictions without a cut.I meant the theory cannot make any predictions without a cut. If the observer is included in the wave function and all we have is the unitarily evolving quantum state, the theory makes no predictions.
I didn't realize how close to this "minimalist interpretation" our interpretation was. We're saying the fundamental explanation for the QM correlations is conservation (of whatever) on average, not trial by trial. What we mean by "fundamental explanation" is that there is nothing deeper to explain this conservation principle. I just updated the arXiv version of the paper (will appear Mon — I keep it updated at users.etown.edu/s/stuckeym/TsirelsonBound.pdf) which contains this:
Thus, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a `causal influence' or hidden variables acting on a trial-by-trial basis to account for that conservation. There are many attempts to add such classical mechanisms, but they are superfluous as far as the physics is concerned. The light postulate of special relativity is a good analogy for our proposed constraint. That is, “the speed of light c is the same in all reference frames'' explains time dilation, length contraction, etc., but there is nothing to explain the light postulate. Likewise, “conservation per no preferred reference frame'' (the most general form of our constraint) explains the Tsirelson bound, but there is nothing to explain that conservation principle (constraint).
That looks very similar to what the minimalist interpretation is calling an ensemble interpretation of the wave function. Further, the measured values proper are what contribute directly to this conversation. That is, whether or not there is some underlying or hidden "true" value of the angular momentum giving rise to what is measured is irrelevant, it is the actual measured values that account for the conservation.
that QM as currently formulated is an incomplete theory.You could put it that way, and I would not argue it. However it depends on how you look at it. I prefer to say right now we have some unresolved issues – progress definitely has been made and research is ongoing. You can say observation is a primitive and all theories have primitives. I am not sure it does resolve it – but is it physics? To me it may be a bit semantic and what philosophers argue about. Personally I tend to side with Dirac and think all theories have issues and we just keep progressing and chipping away – it's very hard to predict where it will lead. I have posted it before, but just for completeness in case someone has not seen it see:
http://philsci-archive.pitt.edu/1614/1/Open_or_Closed-preprint.pdf
Thanks
Bill
Yes, but somewhere above it was said that the theory cannot make predictions without a cut.That statement, taken literally, was wrong. But it's clear (at least to me) that atyy wanted to say that the theory cannot make some of its predictions without a cut.
But if some predictions cannot be made without a cut, then QM as a whole needs a cut.Yes, but somewhere above it was said that the theory cannot make predictions without a cut.
I didn't mean that all predictions can be made without a cut. I said that the theory can make predictions without a cut.But if some predictions cannot be made without a cut, then QM as a whole needs a cut.
Just as real numbers, as a whole, need Dedekind cuts, despite the fact that some real numbers (the rational ones) don't need Dedekind cuts. :wink:
Also Newton's equation of motion doesn't tell me when I look at the point particle I describe. Why should it?Newton's equation is a statement of the form "position of the particle is such and such". It is not a statement of the form "When position of the particle is measured, then position of the particle is such and such".
But quantum mechanics is different. QM does not state that "probability of the position of the particle is such and such". It states that "When position of the particle is measured, then probability of the position of the particle is such and such".
I didn't mean that all predictions can be made without a cut. I said that the theory can make predictions without a cut.
I don't get it. To make it specific let's look at the following. The probability that a photon will decay to a proton is zero. What measurement is needed to make this prediction?It's not a good example. Give me an example in which probability is neither zero nor one.
Yes, the cut is implicit in your expression "to get". This really means "to observe" or "to measure by macroscopic apparatus", so you need a cut in order to distinginsh observers from non-observers or macroscopic from non-macroscopic.I don't get it. To make it specific let's look at the following. The probability that a photon will decay to a proton is zero. What measurement is needed to make this prediction?
I thought that QT can make predictions without any cut. Say, if you smash these particles, then the probability to get those is so and so. No cut and a very spesific prediction. Or something along the lines a black hole will radiate and loose energy, no cut. Or is the cut somewhere implicit.Yes, the cut is implicit in your expression "to get". This really means "to observe" or "to measure by macroscopic apparatus", so you need a cut in order to distinginsh observers from non-observers or macroscopic from non-macroscopic.
In classical mechanics, there is no equivalent difficulty (there is a difficulty from the singularities of GR, but that is different from needing to exclude the observer).Why is that? I mean the part in the parentheses.
No. Also Newton's equation of motion doesn't tell me when I look at the point particle I describe. Why should it?Because in classical mechanics the particle is there whether you look at it or not. In quantum mechanics, the formalism does not assign the particle a position until you look at it.
In quantum mechanics, there is a fundamental difficulty with applying the quantum state to the whole universe including the observer. In classical mechanics, there is no equivalent difficulty (there is a difficulty to include the whole universe from the singularities of GR, but that is different from needing to exclude the observer).
I thought that QT can make predictions without any cut. Say, if you smash these particles, then the probability to get those is so and so. No cut and a very spesific prediction. Or something along the lines a black hole will radiate and loose energy, no cut. Or is the cut somewhere implicit.
Because the point at which you decide to apply the Born rule comes from "outside" the quantum system – the initial quantum state and Schroedinger equation does not tell you when the Born rule is applied.No. Also Newton's equation of motion doesn't tell me when I look at the point particle I describe. Why should it?
Also, it must be admitted (von Neumann knew this, and it is discussed in the textbook by Wiseman and Milburn) the cut is not entirely arbitrary: https://arxiv.org/abs/quant-ph/9712044.I'd say von Neumann was very far away from a physical understanding of QT. His merit is in the proper mathematical formulation. His solipsistic Princeton Interpretation, however, is the worst flavor of the Copenhagen spirit ever.
I've to read the paper to comment it. As far as I see for usual measurements using a usual observable as a pointer there's really no problem with putting the cut anywhere, where a classical description is sensible.
Ok, if the application of the Born rule is a cut, that's fine with me. But why should I call it a cut?Because the point at which you decide to apply the Born rule comes from "outside" the quantum system – the initial quantum state and Schroedinger equation does not tell you when the Born rule is applied.
Ok, if the application of the Born rule is a cut, that's fine with me. But why should I call it a cut?
Hm, where do my experimental colleagues at CERN make some arbitrary cut when constructing their detectors?Also, it must be admitted (von Neumann knew this, and it is discussed in the textbook by Wiseman and Milburn) the cut is not entirely arbitrary: https://arxiv.org/abs/quant-ph/9712044.
The cut isn't in the actual experimental devices; it's in the theory. As I said in post #176: "a cut is required to extract predictions from the theory". Extracting predictions from the theory is not the same as running experiments. And the fact that there is obviously no cut in the experimental devices, whereas you need one to extract predictions from the theory, is just another way of putting what I said in post #176, that QM as currently formulated is an incomplete theory.Hm, I don't need a cut to describe heavy-ion collisions and compare it to experiment. I just calculate the quantities, like dilepton invariant-mass and transverse-momentum spectra and compare them with the experimental results. Of course, these spectra are the collection of data from an ensemble ("the more statistics the better").
But you cannot shift it completely arbitrarily – it cannot be shifted such that the whole universe is quantum, unless perhaps one introduces hidden variables or MWI.That's true. The entire universe cannot be described quantum theortically within the minimal interpretation, because you cannot define what's observable about it, because for that you'd need to prepare many universes in the same initial state to investigate whether the probabilistic meaning of the state is correctly predicting its behavior.
where do my experimental colleagues at CERN make some arbitrary cut when constructing their detectors?The cut isn't in the actual experimental devices; it's in the theory. As I said in post #176: "a cut is required to extract predictions from the theory". Extracting predictions from the theory is not the same as running experiments. And the fact that there is obviously no cut in the experimental devices, whereas you need one to extract predictions from the theory, is just another way of putting what I said in post #176, that QM as currently formulated is an incomplete theory.
Hm, where do my experimental colleagues at CERN make some arbitrary cut when constructing their detectors?When they apply the Born rule :)
Hm, where do my experimental colleagues at CERN make some arbitrary cut when constructing their detectors?
Well, the very fact that proponents of a quantum-classical cut always agree that the cut can shifted arbitrarily shows that the cut is as unnecessary as the aether in classical electromagnetics.But you cannot shift it completely arbitrarily – it cannot be shifted such that the whole universe is quantum, unless perhaps one introduces hidden variables or MWI.
the very fact that proponents of a quantum-classical cut always agree that the cut can shifted arbitrarily shows that the cut is as unnecessary as the aether in classical electromagnetics.No, it doesn't, it shows that quantum mechanics as currently formulated is an incomplete theory. A cut is required to extract predictions from the theory, but the theory does not tell you where to put the cut; practically speaking, physicists put it wherever it works best in making predictions for a particular problem.
Well, the very fact that proponents of a quantum-classical cut always agree that the cut can shifted arbitrarily shows that the cut is as unnecessary as the aether in classical electromagnetics.
But how then is it possible that we construct all our measurement devices based on the known physical laws? Measurement always requires the interaction of the measured object with the measurement device, and in constructing our instruments we assume that this interaction follows the known rules. E.g., most photon detectors assume that in the photon-detector material the laws describing the photoelectric effect are due to quantum electrodynamics.Because the cut can be shifted. You can shift the cut, so that the measuring apparatus is quantum, but without a "classical" or "macroscopic" measuring apparatus to measure the quantum apparatus, quantum theory makes no predictions. In modern terminology, the quantum part of the apparatus is usually called an "ancilla".
Physical interactions between objects follow – so to speak – a law. As Jonathan Allday remarks in "Quantum Reality": "Any interaction between two quantum systems will entangle their states together. Consequently, the entanglement spreads like an infectious disease." Measurement-as-interaction doesn't work, or do I have missed some hidden ideas.But how then is it possible that we construct all our measurement devices based on the known physical laws? Measurement always requires the interaction of the measured object with the measurement device, and in constructing our instruments we assume that this interaction follows the known rules. E.g., most photon detectors assume that in the photon-detector material the laws describing the photoelectric effect are due to quantum electrodynamics. The photon doesn't care whether the atom it hits and "frees" one of its electrons sits in a usual chunk of matter or whether it's part of a photodetector.
Also the very goal of a measurement is in fact to entangle the measured observable of the object with the pointer reasings of the measurment device, so that the pointer readings uniquely measure this observable.
Take the Stern-Gerlach experiment. The measured quantity is a component of the magnetic moment of the particle, and thus you let it run through an appropriately tuned inhomogeneous magnetic field (superimposed with a large practically homogeneous field which determines the direction of the measured component of the magnetic moment). Properly designed this leads to an entanglement of position and the to-be-measured component of the magnetic moment of the particle. The pointer observable here is the position of the particle, which can very easily measured by letting the particle interact with a screen. Using many equaly prepared particles you get a pattern on the screen whose intensity distribution gives the probability distribution for the various values the measured component of the magnetic moment can take. This setup is even simple enough that you can use it as a preparation procedure in the sense of a von Neumann filter measurement (with a careful design of the magnetic field you can make it even very close to an ideal one): You just absorb all the partial beams you don't want and keep only the one beam whose position refers to the wanted value of the component of the magnetic moment. This is all analyzed within quantum theory. Nowhere do I need special rules for interactions and nowhere do I need a classical approximation (although under the discussed conditions the WKB approximation is fully satisfactory).
I thought it has been explained in this thread that the minimal interpretation exclude this assumption (of a possible derivation). By making measurement it axiomatic, any proof would be circular (within this interpretation).There is an argument using whats called coarse gaining to derive the classical world from the quantum – as indeed you must have if it is to be a more fundamental theory than classical:
http://web.physics.ucsb.edu/~quniverse/papers/cop-ext2.pdf
Another way is using the path integral approach to easily explain the PLA from QM and hence classical mechanics. In fact Landau showed that and symmetry is basically all you need to derive classical mechanics, so in a sense all classical mechanics is, is QM in a certain limit – namely the limit where only stationary paths exist because that is the only case where a nearby path doesn't cancel out.
So it is not quite true that the minimalist interpretation doesn't allow one to be more precise about how the classical world emerges from the quantum. And once you do that it's possible to be more precise about exactly what a measurement is than an accepted primitive. But there are still issues with this approach even though a lot of progress has been made. Decoherent Histories for example tries to express QM in terms of histories, which are coarse grainings – the very thing used in deriving the classical world. But it is still an approach that is not totally developed. As an aside it was Feynmans view just before he died.
I would say in probability using the Kolmogerov axioms, event and its axioms is a primitive. From that abstract probability theory is derived. But you can derive things like the law of large numbers and likely other things that shed more light on exactly what this abstract thing probability is. I think the same with observation/measurement as an accepted primitive.
In QM the theory starts with measurement as primitives, leading to the minimalist interpretation, then sharpened up as it is developed. Approaches are around eg Quantum Darwinism, Decoherent Histories, Many Worlds, that try from the start to have the concept of measurement emerge from the theory – but issues still remain.
Thanks
Bill
None of this claims have been made (quite the contrary). Instead you have denied that the "physical law" in question contains an explicit category difference between interaction and measurement. You are also denying that classical law does not need such a dichotomy.Again for me this is the very statement, I don't buy. There is no difference between interaction and measurement. This is vaguely formulated, so maybe I understand you and other proponents of this claim in this thread in a wrong way. For me this says that you and others claim that there's a difference in the interaction of the measured object with the measurement apparatus and all other interactions. This doesn't make sense to me since the same physical laws apply to interactions no matter whether it's the interaction with a measurement apparatus or not. Neither in classical nor in quantum theory is any dichotomy in the applicability of the rules to measurement apparati and other objects. Measurement apparati are made of the same stuff as anything else, and also all physical laws apply to measurement devices as to any other object. That's all I'm claiming. This is also completely independent from which metaphysical additional interpretational ideas you follow on top of the postulates of the minimal statistical interpretation, which is, as its name says, the minimal set of postulates you need to make a physical theory out of the mathematical formalism used in quantum theory.
Maybe we have to reformulate our claims, but I don't know, in which way I can reformulate mine. Perhaps I try to speculate what's the reason for our mutual misunderstanding. One that comes to my mind now is that it may be that you want to give an ontological meaning to the mathematical description used in physical theories, while I have an epistemic view. This concerns particularly the notion of "state" in both classical and quantum theory. In classical theory a state is given by a point in phase space (the "initial state"), in quantum theory it's the statistical operator (in the Heisenberg picture for a closed system it's time-independent). Both phase space in classical mechanics and the operators in Hilbert space are representing properties of observable facts about objects, described in an abstract mathematical way. The relation to physics is given by their relation to observations and measurements of appropriate observables. In classical physics the meaning is deterministic, i.e., all observables (i.e., quantifiable and objectively measurable properties) are always determined, and a probabilistic description is only necessary if we have not complete knowledge about the state of the system. In QT the description is explicitly probabilistic, and there's no other way within QT to describe systems. Due to the mathematically derivable uncertainty relation between incompatible observables it follows immediately that not all observables can be determine, no matter which state the system is in. That's the only profound difference between QT and classical theory: QT is indeterministic in the sense that necessarily not all observables can take definite values, while classical theory is deterministic since all observables always take a determined value.
The problem in this discussion is that @stevendaryl claims that the interactions between an object and another object does not obey the general physical laws if the other object is used as a measurement apparatus to measure an observable on the first object. Now you also claim this. Is there some hope that one day one of you (or any other proponent of this hypothesis) could tell me what this difference may be?
For me it's an absurd idea since all our measurement devices from simple yard sticks to fancy detectors in the LHC are all constructed based on the known physical laws. There's no special law, e.g., in electrodynamics for calculating the effect of a coil in an electrical circuit, when this coil is used in an old-fashioned galvanometer to measure a current or voltage. It obeys the same laws as any other piece of matter containing electric charges and interacting with electromagnetic fields. On a microscopic level it behaves as predicted by QED (of coarse effectively here you can safely use classical electrodynamics as an excellent approximation).Physical interactions between objects follow – so to speak – a law. As Jonathan Allday remarks in "Quantum Reality": "Any interaction between two quantum systems will entangle their states together. Consequently, the entanglement spreads like an infectious disease." Measurement-as-interaction doesn't work, or do I have missed some hidden ideas.
The problem in this discussion is that @stevendaryl claims that the interactions between an object and another object does not obey the general physical laws if the other object is used as a measurement apparatus to measure an observable on the first object. Now you also claim this.None of this claims have been made (quite the contrary). Instead you have denied that the "physical law" in question contains an explicit category difference between interaction and measurement. You are also denying that classical law does not need such a dichotomy.
If it cant be done or the theorem shows it depends crucially on that partition, then we have issues – I think they are probably resolvable – but current theory generally assumes you can do that.I thought it has been explained in this thread that the minimal interpretation exclude this assumption (of a possible derivation). By making measurement it axiomatic, any proof would be circular (within this interpretation).
Then again in solving problems in mechanics such as balls rolling down inclined planes you make the same assumption and I do not think we have theorems for that either – however people generally do not seem to worry about it.I don't understand what you mean. There is absolutely no assumption made in classical mechanics. Measurement is not a special case, and actually does perturb the observed system (the actual source confusion with QM uncertainty principle). But those who care for those effects can use the same classical theory to get perfect/complete knowledge (up to precision) of the (very small) perturbation.
That's another reason why the claim that QM is complete is quite preposterous. "Measurement" of quanta, that Vanhees71 seems to deny the existence of, and instead only consider ensemble to be real (without bothering to define where those ensemble start or end), do something much more dramatic (picking of eigenvalue) that modify the state irreversibly in a huge manner.
Whatever how measurement do this "trick", it happens, on a event by event basis. Because every measurement, classic or quantum, is event base. But QM is incomplete because it need to process many event/measurement before it even can pretend to be "scientific" that is: verifiable.
(Also I will remind that QM have no clue about why the state of the apple move toward the state of the earth)
It has long been my 'feeling' that some issues in QM people worry about are also present in other theories like probability and classical mechanics, however they are generally not worried about in those areas – except maybe by philosophers.I would be interested in such a discussion (maybe in another thread) about those "issues", my feeling is all the weirdness of classical theories a perfectly described by chaos…
The "minimal" interpretation of QM, which is what I thought we were discussing, does treat measurements differently from other interactions. I thought that was the point you were repeatedly making in your discussion with @vanhees71.The problem in this discussion is that @stevendaryl claims that the interactions between an object and another object does not obey the general physical laws if the other object is used as a measurement apparatus to measure an observable on the first object. Now you also claim this. Is there some hope that one day one of you (or any other proponent of this hypothesis) could tell me what this difference may be?
For me it's an absurd idea since all our measurement devices from simple yard sticks to fancy detectors in the LHC are all constructed based on the known physical laws. There's no special law, e.g., in electrodynamics for calculating the effect of a coil in an electrical circuit, when this coil is used in an old-fashioned galvanometer to measure a current or voltage. It obeys the same laws as any other piece of matter containing electric charges and interacting with electromagnetic fields. On a microscopic level it behaves as predicted by QED (of coarse effectively here you can safely use classical electrodynamics as an excellent approximation).
Again, please read what I actually wrote. I didn't say the "real" state of the system changes. I only said the state you use to make predictions about future measurements you make on the system changes. That is true regardless of what interpretation you adopt.Exactly. And the minimalist interpretation assumes only that. Of course when speaking about probabilities you have different views on that – Vanhees and myself take the Frequentest view – as many people in areas that apply probability do – but it is far from the only one. The frequentest view naturally leads to the Ensemble interpretation. As John Baez says much of the argument about QM interpretations is the same as arguments about what probability means:
http://math.ucr.edu/home/baez/bayes.html
Me and Vanhees do not ascribe to the Bayesian view – but really its just philosophy and in applying it makes no difference in practice – well most of the time anyway.
Thanks
Bill
No idea what principles the "collapse postulate" contradicts. I don't understand the wave function as referring to something physically real.It depends on you definition of the collapse postulate, and I know what Vanhees is getting at. We have had long threads about it and we (meaning the mentors) decided so as not to confuse anyone, it's when we know the outcome of an observation and that change in knowledge happens immediately. So please talk about it in that context. Its like the flipping a coin in probability theory – we say nothing about whats going on during that flipping – but speak of the probability of an outcome.
the formalism of QM says nothing physically about whats going on during the observation – just about the probability of the outcome after it. We have speculations like MW, GRW, BM etc, but they are just that – speculations. The ensemble interpretation simply accepts the Born Rule as is with a frequentest type view of probability – it makes no assumption about what is going on during the observation.
Thabks
Bill
So according to the minimal interpretation, there is no physical content to quantum mechanics in the absence of measurements. That's very different from Newtonian physics.There is no physical content of any theory without measurements – if not you cant compare it to experiment so its not testable ie its not science.
The issue with QM is defining, using nothing but QM itself, what a measurement its. Great progress has been made is doing that – but some issues still remain eg some key theorems are still missing saying that it doesn't matter how you 'partition' a quantum system between what is doing the observing, what is being observed, and the environment, and any other thing you may come up with. If it cant be done or the theorem shows it depends crucially on that partition, then we have issues – I think they are probably resolvable – but current theory generally assumes you can do that. Then again in solving problems in mechanics such as balls rolling down inclined planes you make the same assumption and I do not think we have theorems for that either – however people generally do not seem to worry about it. It has long been my 'feeling' that some issues in QM people worry about are also present in other theories like probability and classical mechanics, however they are generally not worried about in those areas – except maybe by philosophers.
Thanks
Bill
Suppose you start in state ##|Arangle## and make a transition to either state ##|Brangle## or ##|Crangle## and then want to compute the probability that you end up in state ##|Drangle##.Note also that you are implicitly assuming that this computation is made before the result of any measurement at the B/C stage is known. If there is a measurement at the B/C stage, and you know the result of that measurement, you just compute the probability ##P_{BD}## or ##P_{CD}##, depending on which result was observed.
If you say that it only happens when you make a measurement would be treating measurements differently than other interactions.The "minimal" interpretation of QM, which is what I thought we were discussing, does treat measurements differently from other interactions. I thought that was the point you were repeatedly making in your discussion with @vanhees71.
If you are not assuming collapse, then you can't change the state based on what you observed.Again, please read what I actually wrote. I didn't say the "real" state of the system changes. I only said the state you use to make predictions about future measurements you make on the system changes. That is true regardless of what interpretation you adopt.
Suppose you start in state ##|Arangle## and make a transition to either state ##|Brangle## or ##|Crangle## and then want to compute the probability that you end up in state ##|Drangle##."Make a transition" is ambiguous. Do you measure the transition–do you observe either state ##|Brangle## or ##|Crangle##? Or does no measurement take place, just a unitary evolution that assigns nonzero amplitudes to states ##|Brangle## and ##|Crangle##?
If instead you assume collapse, then you leave out the interference term.No, if you measure which intermediate state occurs, ##|Brangle## or ##|Crangle##, then you leave out the interference term. Otherwise you don't.
For example, say ##A## is the state of a source that emits quanta that will pass through a double slit and then hit a detector screen; ##B## is the state of passing through the left slit; ##C## is the state of passing through the right slit; ##D## is the state of ending up at a particular location on the detector screen. If you measure which slit the quanta pass through, there is no interference; if you don't, there is. That is true whether or not you adopt a collapse interpretation; it's part of the basic math of QM.
In your example with spin up and spin down, you are measuring the spin, so there is no interference.
If you want to include the measuring devices and the environment in all of this, and you are measuring which intermediate state, ##B## or ##C##, occurs (e.g., you are measuring spin up or spin down) before going on to state ##D##, then the only source of "interference" terms comes from inaccuracy in the records left by the measuring devices–i.e., what you refer to here as being practically impossible:
It's impossible (practically) that there could be a record of my measuring spin-up if I actually measured spin-down.But this is not the same as, for example, interference in the double slit experiment when you don't measure which slit the quanta go through.
If you mean, this happens once when a measurement is made and its result is recorded, yes, I guess you could look at it this way.If you say that it only happens when you make a measurement would be treating measurements differently than other interactions. You could say, instead that it's true for every macroscopic state.
If you mean, this is happening all the time and explains why measurement results on the system are probabilitistic, no, I don't think that works, because once you've measured the system to be in a particular eigenstate, you use that eigenstate as your starting point for future predictions, not the probabilistic mixture you were using before.That's what you would do if you're using the collapse hypothesis. If you are not assuming collapse, then you can't change the state based on what you observed.
However, in practice, this won't make any difference, because measurements are irreversible.
Suppose you start in state ##|Arangle## and make a transition to either state ##|Brangle## or ##|Crangle## and then want to compute the probability that you end up in state ##|Drangle##.
If you don't assume collapse, then the probability is given by the following:
Then the probability to go from ##A## to ##D## is given by:
If instead you assume collapse, then you leave out the interference term. However, if states ##B## and ##C## are macroscopically distinguishable, then the interference term is essentially zero, anyway.
If ##B## is the state in which "I measured spin-up", and ##C## is the state in which "I measured spin-down", then there is no final macroscopically determinate state ##D## such that both ##P_{BD}## and ##P_{CD}## is significantly different from zero. In state ##D##, either there will be a record of my having measured spin-up, or there will be a record of having measured spin-down. It's impossible (practically) that there could be a record of my measuring spin-up if I actually measured spin-down.
So the macro state just nondeterministically changes from one state to anotherIf you mean, this happens once when a measurement is made and its result is recorded, yes, I guess you could look at it this way.
If you mean, this is happening all the time and explains why measurement results on the system are probabilitistic, no, I don't think that works, because once you've measured the system to be in a particular eigenstate, you use that eigenstate as your starting point for future predictions, not the probabilistic mixture you were using before.
If ##|Arangle## and ##|Brangle## are macroscopically different, then the difference between these two density matrices is practically unobservable.Agreed. But that's not the issue I was trying to get at.
Even once you've dropped the interference terms, you still will be switching density matrices once you know the actual measurement result. At that point, you aren't using ##|alpha|^2 |Aranglelangle A| + |beta|^2 |Brangle langle B|## to predict future measurement results; you're using either ##|Aranglelangle A|## or ##|Brangle langle B|##. And the latter two states are not mixtures (nor are they superpositions).
That's why I'm saying that I think there is something screwy about the minimal interpretation.I wouldn't say it's "screwy", just limited. In the minimal interpretation, when we say which state is "real" (as I did in previous posts), all we mean is that we are going to use that state to make predictions about future measurements on the system. We're not making any ontological claim about what state the system is "really" in; that is interpretation dependent. We're just describing the mathematical procedure for making predictions.
The distinction between superpositions and mixed states is mathematically described in terms of interference terms. But for macroscopically distinguishable states, the interference terms are completely negligible. So in practice, there is no detectable distinction.To elaborate, a superposition of ##alpha |Arangle + beta |Brangle## corresponds to a density matrix ##|alpha|^2 |Aranglelangle A| + alpha^* beta |Brangle langle A| + beta^* alpha |Aranglelangle B| + |beta|^2 |Brangle langle B|##
In contrast, the density matrix for the system is in state A with probability ##|alpha|^2## and the system is in state B with probability ##|beta|^2## is given by:
##|alpha|^2 |Aranglelangle A| + |beta|^2 |Brangle langle B|##.
If ##|Arangle## and ##|Brangle## are macroscopically different, then the difference between these two density matrices is practically unobservable.
Again, if you say "the system is either in one state or the other state, with probabilities given by the square of the amplitude", then you are saying the system is not in a superposition. And I've tried to clarify what that means in the first part of this post.The distinction between superpositions and mixed states is mathematically described in terms of interference terms. But for macroscopically distinguishable states, the interference terms are completely negligible. So in practice, there is no detectable distinction.
And if you do that, then you are saying the system is not in the state "superposition of two possibilities". It's in either the "first possibility" state or the "second possibility" state, with the respective probabilities you give of being in each. And when you make predictions about the results of future measurements on the system, you will use one of those two states (whichever one actually gets observed when the measurement is made). You won't use the state "superposition of two possibilities".That's why I'm saying that I think there is something screwy about the minimal interpretation. If you don't have a wave function collapse, or something equivalent, then following a measurement you end up in an entangled state, not a state where measurement results have definite outcomes.
However, I think it is actually consistent (although weird, for a reason I'll get to in a second) to treat a superposition of macroscopically distinguishable states as a mixed state, where the amplitudes give the probabilities of the "true" state being this or that.
Mathematically, we can describe it this way: Let ##j## range over some coarse-grained partitioning of the state of the composite system, and let ##Pi_j## be the corresponding projection operator. Then we can just declare that the probability of being in macro state ##j## given that the composite is initially in state ##|psirangle## is:
##P_j(t) = langle psi| e^{iHt} Pi_j e^{-iHt} |psirangle##
So the macro state just nondeterministically changes from one state to another, with probabilities controlled by the microstate
##|psi(t)rangle = e^{-iHt} |psirangle##
I think that's a consistent interpretation, although it's weird, in that the microstate affects the macrostate, but not vice-versa.
If you describe the measurement process itself as a quantum-mechanical interaction, then what you will find is that the combination measured-system-plus-measuring-device-plus-environment will evolve into a superposition of a number of possibilities.Agreed.
You can interpret this as "there is a probability of ##|alpha|^2## for the first possibility and a probability of ##|beta|^2## of the second possibility.And if you do that, then you are saying the system is not in the state "superposition of two possibilities". It's in either the "first possibility" state or the "second possibility" state, with the respective probabilities you give of being in each. And when you make predictions about the results of future measurements on the system, you will use one of those two states (whichever one actually gets observed when the measurement is made). You won't use the state "superposition of two possibilities".
That's equivalent. You're interpreting "the system is a superposition of macroscopically distinguishable possibility with amplitudes given by Hamiltonian evolution" as "the system is either in one state or the other state, with probabilities given by the square of the amplitude".No, I'm not. Please read what I actually wrote. The words "you cannot describe the system as being in a superposition" are right there in what you quoted from me. "Cannot" does not mean "equivalent".
Again, if you say "the system is either in one state or the other state, with probabilities given by the square of the amplitude", then you are saying the system is not in a superposition. And I've tried to clarify what that means in the first part of this post.
I think this is a misuse of the term "superposition". That term never means that "the system is either in this state or that state, with such-and-such probability". That is a "mixture".
The question is whether a superposition (defined as I just have) of macroscopically distinguishable states is even possible. The MWI says it is; a collapse interpretation says it isn't (collapse always removes all but one term in the superposition before that happens).I couldn't agree more!
First of all you have to tell superposition of which vectors. Usually one takes an observable and decomposes the pure state, in terms of a normalized vector
$$|Psi rangle=sum_a Psi_a |a rangle,$$
where ##|a rangle## is a complete orthonormalized set of eigenvectors of the representing self-adjoint operator of the quantity measured. The state is then given by the statistical operator
$$hat{rho}=|Psi rangle langle Psi|.$$
Then it's of course wrong to say "the system is in a state where the observable ##A## takes all the possible values ##a## at the same time" (to make it clear again this sentence is WRONG, no matter how often it is repeated even in real textbooks, not only in popular writings!). The right thing to say is that for the quantum system prepared in this state the probability to find the value ##a## when you measure the observable ##A## is given by ##P_a=|Psi_a|^2=langle a|hat{rho}|a rangle## (here for simplicity I assume the case that ##hat{A}## is non-degenerate, i.e., I assume that all eigenspaces are one-dimensional).
Consequently this implies that the system has a determined value of the observable ##A## being ##a## if and only if ##P_a=1## and ##P_{a'}=0## for all ##a' neq a##. This implies that ##|Psi rangle=|a rangle## and the state is ##hat{rho}=|a rangle langle a|##.
If this is not the case, the observable ##A##'s value is indetermined, and the probability to find any of the possible values ##a## is ##P_a##. There's no other meaning (within the minimal statistical interpretation) than this, and as far as I know it's the meaning which is testable in the lab on doing measurements of ##A## on ensembles of equally prepared systems, using the usual statistical analysis to test probabilistic predictions.
Also the final statement is completely correct. If you say it's in any case in a state where ##A## has a determined value, but it's not known which value but you know there are probabilities ##P_a## for each value, then the correct association of a state, if no other information is given, is
$$hat{rho}'=sum_a P_a |a rangle langle a|.$$
The thought-experimental realization is that Alice prepares an ensemble of systems providing Bob with the corresponding single systems. This means that Alice prepares each single member of the ensemble in a state described by the statistical operator ##hat{P}_a =|a rangle langle a|## and she sends a fraction ##P_a## of single systems for each determined value ##A## to Bob. Of course ##hat{rho}' neq hat{rho}=|Psi rangle langle Psi|##. Although Bob cannot distinguish the two states by just measuring ##A##, the states are different, and you can in principle find the difference by more fancy observations (see the excellent chapter on "state preparation and determination" in Ballentine's textbook).
No, you have to say that, once the alternatives become macroscopically distinguishable, only one of the alternatives is real, and therefore you cannot describe the system as being in a superposition any more.That's equivalent. You're interpreting "the system is a superposition of macroscopically distinguishable possibility with amplitudes given by Hamiltonian evolution" as "the system is either in one state or the other state, with probabilities given by the square of the amplitude".
If you don't treat macroscopic systems as different than microscopic systems, from the point of view of evolution, then the system will evolve into a superposition of macroscopically distinguishable alternatives. It's inevitable.
I'm talking about the implications of the minimal interpretation in which you try to maintain both (1) the claim that macroscopic systems evolve in the same way that microscopic systems do, and (2) the probabilities of measurement alternatives are given by the Born rule. It seems to me that there is no way to have both unless you interpret macroscopic superpositions as mixtures, essentially.