Why the Quantum | A Response to Wheeler’s 1986 Paper
Wheeler’s opening statement in his 1986 paper, “How Come the Quantum?” holds as true today as it did then [1]
The necessity of the quantum in the construction of existence: out of what deeper requirement does it arise? Behind it all is surely an idea so simple, so beautiful, so compelling that when — in a decade, a century, or a millennium — we grasp it, we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?
In this Insight, I will answer Wheeler’s question per its counterpart in quantum information theory (QIT), “How come the Tsirelson bound?” Let me start by explaining the Tsirelson bound and its relationship to the Bell inequality, then it will be obvious what that has to do with Wheeler’s question, “How Come the Quantum?” The answer (the Tsirelson bound is a consequence of conservation per no preferred reference frame (NPRF)) may surprise you with its apparent simplicity, but that simplicity belies a profound mystery, as we will see.
The Tsirelson bound is the spread in the Clauser-Horne-Shimony-Holt (CHSH) quantity
\begin{equation}\langle a,b \rangle + \langle a,b^\prime \rangle + \langle a^\prime,b \rangle – \langle a^\prime,b^\prime \rangle \label{CHSH1}\end{equation}
created by quantum correlations. Here, we consider a pair of entangled particles (or “quantum systems” or “quantum exchanges of momentum”). Alice makes measurements on one of the two particles with her measuring device set to ##a## or ##a^\prime## while Bob makes measurements on the other of the two particles with his measuring device set to ##b## or ##b^\prime##. There are two possible outcomes for either Bob or Alice in either of their two possible settings given by ##i## and ##j##. For measurements at ##a## and ##b## we have for the average of Alice’s results multiplied by Bob’s results on a trial-by-trial basis
\begin{equation}\langle a,b \rangle = \sum (i \cdot j) \cdot P(i,j \mid a,b) \label{average}\end{equation}
That’s a bit vague, so let me supply some actual physics. The two entangled states I will use are those which uniquely give rise to the Tsirelson bound [2-4] , i.e., the spin singlet state and the ‘Mermin photon state’ [5]. The spin singlet state is ##\frac{1}{\sqrt{2}} \left(\mid ud \rangle – \mid du \rangle \right)## where ##u##/##d## means the outcome is displaced upwards/downwards relative to the north-south pole alignment of the Stern-Gerlach (SG) magnets (Figure 1).
 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
This state obtains due to conservation of angular momentum at the source as represented by momentum exchange in the spatial plane P orthogonal to the source collimation (“up or down” transverse). This state might be produced by the dissociation of a spin-zero diatomic molecule [6] or the decay of a neutral pi meson into an electron-positron pair [7], processes which conserve spin angular momentum. For more information about the spin singlet state and the spin triplet states, see this Insight.
The Mermin state for photons is ##\frac{1}{\sqrt{2}} \left(\mid VV \rangle + \mid HH \rangle \right)## where ##V## means the there is an outcome (photon detection) behind one of the coaligned polarizers and ##H## means there is no outcome behind one of the co-aligned polarizers. This state obtains due to conservation of angular momentum at the source as represented by momentum exchange along the source collimation (“yes” or “no” longitudinal). Dehlinger and Mitchell created this state by laser inducing spontaneous parametric downconversion in beta barium borate crystals [8], a process that conserves spin angular momentum as represented by the polarization of the emitted photons. At this point we will focus the discussion on the spin single state for total anti-correlation, since everything said of that state can be easily transferred to the Mermin photon state.
Let us investigate what Alice and Bob discover about these entangled states in the various contexts of their measurements (Figure 2). Alice’s detector responds up and down with equal frequency regardless of the orientation ##\alpha## of her SG magnet. This is in agreement with the relativity principle, aka “no preferred reference frame” (NPRF), where different SG magnet orientations relative to the source constitute different “reference frames” in quantum mechanics just as different velocities relative to the source constitute different “reference frames” in special relativity (see this Insight).
Figure 2. Alice and Bob making spin measurements in the xz plane on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors.
Bob observes the same regarding his SG magnet orientation ##\beta##. Thus, the source is rotationally invariant in the spatial plane P orthogonal to the source collimation. When Bob and Alice compare their outcomes, they find that their outcomes are perfectly anti-correlated (##ud## and ##du## with equal frequency) when ##\alpha – \beta = \theta = 0## (Figure 3). This is consistent with conservation of angular momentum per classical mechanics between the pair of detection events (again, this fact defines the state). The degree of that anti-correlation diminishes as ##\theta \rightarrow \frac{\pi}{2}## until it is equal to the degree of correlation (##uu## and ##dd##) when their SG magnets are at right angles to each other. In other words, whenever the SG magnets are orthogonal to each other anti-correlated and correlated outcomes occur with equal frequency, i.e., conservation of angular momentum in one direction is independent of the angular momentum changes in any orthogonal direction. Thus, we wouldn’t expect to see more correlation or more anti-correlation based on conservation of angular momentum for transverse results in the plane P when the SG magnets are orthogonal to each other. As we continue to increase the angle ##\theta## beyond ##\frac{\pi}{2}## the anti-correlations continue to diminish until we have totally correlated outcomes when the SG magnets are anti-aligned. This is also consistent with conservation of angular momentum, since the totally correlated results when the SG magnets are anti-aligned represent momentum exchanges in opposite directions in the plane P just as when the SG magnets are aligned, it is now simply the case that what Alice calls up, Bob calls down and vice-versa.
The counterpart for the Mermin photon state is simply that angular momentum conservation is evidenced by ##VV## or ##HH## outcomes for coaligned polarizers. When the polarizers are at right angles you have only ##VH## and ##HV## outcomes, which is still totally consistent with conservation of angular momentum as ‘not ##H##’ implies ##V## and vice-versa [8]. In other words, a polarizer does not have a ‘north-south’ distinction (longitudinal rather than transverse momentum exchange). In particular, having rotated either or both polarizers by ##\pi## one should obtain precisely ##VV## or ##HH## outcomes again.
Nothing is particularly mysterious about the entangled states for electron spin or photon polarization described here so far because we have been thinking as if conservation of angular momentum holds for each experimental trial, as in classical mechanics. Truth is, since Alice and Bob can only measure +1 or -1 (quantum exchange of momentum per NPRF), we can only get conservation of angular momentum in any particular trial when their SG magnets/polarizers are co-aligned. And, we cannot use classical probability theory to account for the conservation of angular momentum on average.
In particular, the probability that Alice and Bob will measure ##uu## or ##dd## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityuu}\end{equation}
And, the probability that Alice and Bob will measure ##ud## or ##du## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityud}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##u##) and -1 (##d##) gives Eq. (\ref{CHSH1}) of
\begin{equation}-\cos(a – b) -\cos(a – b^\prime) -\cos(a^\prime – b) +\cos(a^\prime – b^\prime) \label{CHSHspin}\end{equation}
Choosing ##a = \pi/4##, ##a^\prime = -\pi/4##, ##b = 0##, and ##b^\prime = \pi/2## minimizes Eq. (\ref{CHSHspin}) at ##-2\sqrt{2}## (the Tsirelson bound).
Likewise, for the Mermin photon state we have
\begin{equation}P_{VV} = P_{HH} = \frac{1}{2} \mbox{cos}^2 \left(\alpha – \beta \right) \label{probabilityVV}\end{equation}
and
\begin{equation}P_{VH} = P_{HV} = \frac{1}{2} \mbox{sin}^2 \left(\alpha – \beta \right) \label{probabilityVH}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##V##) and -1 (##H##) gives Eq. (\ref{CHSH1}) of
\begin{equation}\cos2(a – b) +\cos2(a – b^\prime) +\cos2(a^\prime – b) -\cos2(a^\prime – b^\prime) \label{CHSHmermin}\end{equation}
Using ##a = \pi/8##, ##a^\prime = -\pi/8##, ##b = 0##, and ##b^\prime = \pi/4## maximizes Eq. (\ref{CHSHmermin}) at ##2\sqrt{2}## (the Tsirelson bound). So, we have two mysteries.
First, as explained by Mermin [5], suppose you restrict Alice and Bob’s measurement angles ##\alpha## and ##\beta## to three possibilities, setting 1 is ##0^o##, setting two is ##120^o##, and setting three is ##-120^o##. Eq. (\ref{probabilityud}) says the probability of getting opposite results is 1 when ##\alpha = \beta## (1/2 ##ud## and 1/2 ##du##) and 1/4 otherwise (1/8 ##ud## and 1/8 ##du##). Now, if the source emits particles with definite properties that account for their outcomes in the three possible measurement settings, and we have to get total anti-correlation for like settings, then the particles’ so-called “instruction sets” must be opposite for each of the three settings. For example, suppose we have 1(##u##)2(##u##)3(##d##) for Alice and 1(##d##)2(##d##)3(##u##) for Bob. That guarantees the total anti-correlation for like settings, i.e., 11 gives ##ud##, 22 gives ##ud##, and 33 gives ##du##. And, for unlike settings we get anti-correlation in two combinations, i.e., 12 gives ##ud## and 21 gives ##ud##. In fact, for any instruction set with two ##u## and one ##d## we get anti-correlation for unlike settings in two of the six possible unlike combinations (12,13,21,23,31,32). The only other way to make a pair of instruction sets is to have one with all ##u## and the other with all ##d##. In that case, we get anti-correlation for all six unlike combinations. That means the instruction sets necessary to guarantee anti-correlation for like settings lead to an overall anti-correlation greater than 2/6 for unlike settings, which is greater than the quantum probability for anti-correlation in unlike settings of 1/4. This is Mermin’s version of the Bell inequality [9] (fraction of anti-correlated outcomes for unlike settings must be greater than 2/6) and the manner by which it is violated by quantum correlations (1/4 is less than 2/6). Thus, instruction sets (“counterfactual definiteness”) assumed by classical probability theory cannot account for quantum correlations in this case.
The counterpart to this for the CHSH quantity is that classical correlations give a range of -2 to 2 for the CHSH quantity (“CHSH-Bell inequality”). And, as we saw above, the Tsirelson bound violates the CHSH-Bell inequality. Experiments show that the quantum results can be achieved (violating the Bell inequality), ruling out an explanation of these correlated momentum exchanges via instruction sets per classical probability theory.
The second mystery is that even in cases where we don’t violate the Bell inequality, e.g., ##a = b = 0## and ##a^\prime = b^\prime = \pi/2## which give a CHSH value of 0, we still have conservation of angular momentum. Why is that mysterious? Well, it’s not when the SG magnets are co-aligned, since in those cases we always get a +1 outcome and a -1 outcome for a total of zero. But, in trials where ##\alpha – \beta = \theta## does not equal zero, we need either Alice or Bob, at minimum, to measure something less than 1 to conserve angular momentum. For example, if Alice measures +1, then Bob must measure ##-\cos{\theta}## to conserve angular momentum for that trial. But, again, Alice and Bob only measure +1 or -1 (quantum exchange of momentum per NPRF, which uniquely distinguishes the quantum joint distribution from its classical counterpart [10]), so that can’t happen (Figure 4). What does happen? We conserve angular momentum on average in those trials.
It is easy to see how this follows by starting with total angular momentum of zero for binary (quantum) outcomes +1 and -1 (I am suppressing the factor of ##\hbar/2## and I’m referring to the spin singlet state here [11], Figure 3).

Figure 3. Outcomes (yellow dots) in the same reference frame, i.e., outcomes for the same measurement (blue arrows represent SG magnet orientations), for the spin singlet state explicitly conserve angular momentum.
Alice and Bob both measure +1 and -1 results with equal frequency for any SG magnet angle (NPRF) and when their angles are equal they obtain different outcomes giving total angular momentum of zero. The case (a) result is not difficult to understand via conservation of angular momentum, because Alice and Bob’s measured values of spin angular momentum cancel directly when ##\alpha = \beta##, that defines the spin singlet state. But, when Bob’s SG magnet is rotated by ##\alpha – \beta = \theta## relative to Alice’s, the situation is not as clear (Figure 6).
In classical physics, one would say the projection of the angular momentum vector of Alice’s particle ##\vec{S}_A = +1\hat{a}## along ##\hat{b}## is ##\vec{S}_A\cdot\hat{b} = +\cos{(\theta)}## where again ##\theta## is the angle between the unit vectors ##\hat{a}## and ##\hat{b}## (Figure 2). From Alice’s perspective, had Bob measured at the same angle, i.e., ##\beta = \alpha##, he would have found the angular momentum vector of his particle was ##\vec{S}_B = -1\hat{a}##, so that ##\vec{S}_A + \vec{S}_B = \vec{S}_{Total} = 0##. Since he did not measure the angular momentum of his particle at the same angle, he should have obtained a fraction of the length of ##\vec{S}_B##, i.e., ##\vec{S}_B\cdot\hat{b} = -1\hat{a}\cdot\hat{b} = -\cos{(\theta)}## (Figure 4).

Figure 4. The projection of the angular momentum of Bob’s particle ##\vec{S}_B## along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum due to NPRF.
Of course, Bob only ever obtains +1 or -1 per NPRF, so Bob’s outcomes can only average the required ##-\cos{(\theta)}##. Thus, NPRF dictates
\begin{align*}
P_{uu} + P_{ud} & = \frac {1}{2} \\
P_{ud} + P_{dd} & = \frac {1}{2},
\end{align*}
These equations now allow us to uniquely solve for the joint probabilities
\begin{equation}
P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\theta}{2} \right) \label{QMjointLike}
\end{equation}
and
\begin{equation}
P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\theta}{2} \right) \label{QMjointUnlike}
\end{equation}
\begin{equation}
\overline{BA-} = 2P_{du}(+1) + 2P_{dd}(-1) = \cos (\theta) \label{BA-}
\end{equation}
Using Eqs. (\ref{BA+}) and (\ref{BA-}) in Eq. (\ref{consCorrel}) we obtain
\begin{equation}
\langle \alpha,\beta \rangle = \frac{1}{2}(+1)_A(-\mbox{cos} \left(\theta\right)) + \frac{1}{2}(-1)_A(\mbox{cos} \left(\theta\right)) = -\mbox{cos} \left(\theta\right) \label{consCorrel2}
\end{equation}
which is precisely the correlation function for a spin singlet state found using the joint probabilities per quantum mechanics. To see that we simply use Eqs. (\ref{probabilityuu}) and (\ref{probabilityud}) in Eq. (\ref{average}) to get
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)(-1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(+1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) +\\ &(+1)(+1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(-1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \\ &= -\mbox{cos} \left(\alpha – \beta \right) = -\mbox{cos} \left(\theta \right)
\end{split}
\label{correl}\end{equation}
Thus, “average-only” conservation maps beautifully to our classical expectation (Figures 6 & 7). Since the angle between SG magnets ##\theta## is twice the angle between Hilbert space measurement bases, this result easily generalizes to conservation per NPRF of whatever the measurement outcomes represent when unlike outcomes entail conservation in the symmetry plane [15] (see this Insight on the Bell spin states). However, again, none of the formalism of quantum mechanics is used in obtaining Eq. (\ref{consCorrel2}) or our quantum state Eqs. (\ref{QMjointLike}) & (\ref{QMjointUnlike}). In deriving the quantum correlation function and quantum state in this fashion, we assumed only NPRF.For the Mermin photon state, conservation of angular momentum is established by ##V## (designated by +1) and ##H## (designated by -1) results through a polarizer. When the polarizers are co-aligned Alice and Bob get the same results, half pass and half no pass. Thus, conservation of angular momentum is established by the intensity of the electromagnetic radiation applied to binary outcomes for various polarizer orientations. As with spin angular momentum, this is classical thinking applied to binary outcomes per conservation of angular momentum. Again, grouping Alice’s results into +1 and -1 outcomes we see that she would expect to find ##[\mbox{cos}^2\theta – \mbox{sin}^2\theta]## at ##\theta## for her +1 results and ##[\mbox{sin}^2\theta – \mbox{cos}^2\theta]## for her -1 results. Since Bob measures the same thing as Alice for conservation of angular momentum, those are Bob’s averages when his polarizer deviates from Alice’s by ##\theta##. Therefore, the correlation of results for conservation of angular momentum is given by
\begin{equation}\langle \alpha,\beta \rangle =\frac{(+1_A)(\mbox{cos}^2\theta – \mbox{sin}^2\theta)}{2} + \frac{(-1_A)(\mbox{sin}^2\theta – \mbox{cos}^2\theta)}{2} = \cos{2\theta} \label{merminconserve}\end{equation}
which is precisely the correlation given by quantum mechanics.As before, we need to find ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## so we need four independent conditions. Normalization and ##P_{VH} = P_{HV}## are the same as for the spin case. The correlation function
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)_A(+1)_BP_{VV} + (+1)_A(-1)_BP_{VH} + \\&(-1)_A(+1)_BP_{HV} + (-1)_A(-1)_BP_{HH}\label{correlFn2}
\end{split}
\end{equation}
along with our conservation principle represented by Eq. (\ref{merminconserve}) give
\begin{equation}
P_{VV} – P_{VH} = -\frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
and
\begin{equation}
P_{HV} – P_{HH} = \frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
Solving these four equations for ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## gives precisely Eqs. (\ref{probabilityVV}) & (\ref{probabilityVH}).Notice that since the angle between polarizers ##\alpha – \beta## equals the angle between Hilbert space measurement bases, this result immediately generalizes to conservation per NPRF of whatever the outcomes represent when like outcomes entail conservation in the symmetry plane [15] (again, see this Insight on the Bell spin states).Since the quantum correlations violate the Bell inequality to the Tsirelson bound and satisfy conservation per NPRF while the classical correlations do not violate the Bell inequality, the classical correlations do not satisfy conservation per NPRF. Experiments of course tell us that Nature obeys the quantum correlations and therefore the conservation per NPRF.

Figure 5. A spatiotemporal ensemble of 8 experimental trials for the Bell spin states showing Bob’s outcomes corresponding to Alice‘s ##+1## outcomes when ##\theta = 60^\circ##. Angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{60^\circ}=\frac{1}{2}##). It is impossible for angular momentum to be conserved explicitly in each trial since the measurement outcomes are binary (quantum) with values of ##+1## (up) or ##-1## (down) per no preferred reference frame. The conservation principle at work here assumes Alice and Bob’s measured values of angular momentum are not mere components of some hidden angular momentum with variable magnitude. That is, the measured values of angular momentum are the angular momenta contributing to this conservation.
Figure 6. For the spin singlet state (S = 0). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from –1 (totally down, arrow bottom) to 0 to +1 (totally up, arrow tip). This obtains per conservation of angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of angular momentum on average, because they only measure +1/-1, never a fractional result. Thus, just as with the light postulate of special relativity, we see that no preferred reference frame leads to counterintuitive results (see this Insight).
Figure 7. The situation is similar for the spin triplet states where outcomes agree for the same measurement in the plane containing the conserved angular momentum vector (S = 1). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to –1 (totally down, arrow bottom). This obtains per conservation of angular momentum on average in the plane containing the S = 1 spin angular momentum in accord with no preferred reference frame. See this Insight for details.
So, while conservation per NPRF sounds like a very reasonable constraint on the distribution of quantum exchange of momentum (+1 or -1, no fractions), we still do not have any causal mechanism to explain the outcomes of any particular trial when the SG magnets/polarizers are not co-aligned (Figure 4). And, as I showed above, we cannot use instruction sets per classical probability theory to account for the Tsirelson bound needed to explain the conservation of angular momentum on average. Thus, while we have a very reasonable constraint on the distribution of entangled quantum exchanges (conservation of angular momentum), that constraint has no compelling dynamical counterpart, i.e., no consensus causal mechanism to explain the outcome of any particular trial when the SG magnets/polarizers are not co-aligned and no counterfactual definiteness to explain why conservation of angular momentum is conserved on average. What we have is a “principle” account of entanglement and the Tsirelson bound (see this Insight). I will return to this point after showing how so-called “superquantum correlations” fail to satisfy this constraint as well.
There are QIT correlations that not only violate the Bell inequality, but also violate the Tsirelson bound. Since these correlations violate the Tsirelson bound, they are called “superquantum correlations.” The reason QIT considers these correlations reasonable (no known reason to reject their possibility) is because they do not violate superluminal communication, i.e., the joint probabilities don’t violate the no-signaling condition
\begin{equation}\begin{split}P(A \mid a\phantom{\prime},b\phantom{\prime}) &= P(A \mid a\phantom{\prime}, b^\prime)\\
P(A \mid a^\prime,b\phantom{\prime}) &= P(A \mid a^\prime, b^\prime)\\
P(B \mid a\phantom{\prime},b\phantom{\prime}) &= P(B \mid a^\prime, b\phantom{\prime})\\
P(B \mid a\phantom{\prime},b^\prime) &= P(B \mid a^\prime, b^\prime )\end{split}\label{nosig}\end{equation}
This means Alice and Bob measure the same outcomes regardless of each other’s settings. If this wasn’t true, Alice and Bob would notice changes in the pattern of their outcomes as the other changed their measurement settings. Since the measurements for each trial can be spacelike separated that would entail superluminal communication.
The Popescu-Rohrlich (PR) joint probabilities
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
produce a value of 4 for Eq. (\ref{CHSH1}), the largest of any no-signaling possibilities. Thus, the QIT counterpart to Wheeler’s question, “How Come the Quantum?” is “Why the Tsirelson bound?” [12-14]. In other words, is there any compelling principle that rules out superquantum correlations as conservation of angular momentum ruled out classical correlations? Let us look at Eq. (\ref{PRcorr}) in the context of our spin singlet and Mermin photon states. Again, we will focus the discussion on the spin singlet state and allude to the obvious manner by which the analysis carries over to the Mermin photon state.
The last PR joint probability certainly makes sense if ##a^\prime = b^\prime##, i.e., the total anti-correlation implying conservation of angular momentum, so let us start there. The third PR joint probability makes sense for ##b = \pi + b^\prime##, where we have conservation of angular momentum with Bob having flipped his coordinate directions. Likewise, then, the second PR joint probability makes sense for ##a = \pi + a^\prime##, where we have conservation of angular momentum with Alice having flipped her coordinate directions. All of this is perfectly self consistent with conservation of angular momentum as we described above, since ##a^\prime## and ##b^\prime## are arbitrary per rotational invariance in the plane P. But now, the first PR joint probability is totally at odds with conservation of angular momentum. Both Alice and Bob simply flip their coordinate directions, so we should be right back to the fourth PR joint probability with ##a^\prime \rightarrow a## and ##b^\prime \rightarrow b##. Instead, the first PR joint probability says that we have total correlation (maximal violation of conservation of angular momentum) rather than total anti-correlation per conservation of angular momentum, which violates every other observation. In other words, the set of PR observations violates conservation of angular momentum in a maximal sense. To obtain the corresponding argument for angular momentum conservation per the correlated outcomes of the Mermin photon state, simply start with the first PR joint probability and show the last PR joint probability maximally violates angular momentum conservation.
To find the degree to which superquantum correlations violate our constraint, replace the first PR joint probability with
\begin{equation}\begin{split}&p(1,1 \mid a,b) = C \\
&p(-1,-1 \mid a, b) = D \\
&p(1,-1 \mid a,b) = E \\
&p(-1,1 \mid a, b) = F \\ \end{split} \label{PRcorrMod}\end{equation}
The no-signaling condition Eq. (\ref{nosig}) in conjunction with the second and third PR joint probabilities gives ##C = D## and ##E = F##. That in conjunction with normalization ##C + D + E + F =1## and P(anti-correlation) + P(correlation) = 1 means total anti-correlation (##E = F = 1/2##, ##C = D = 0##) is the conservation of angular momentum per the quantum case while total correlation (##E = F = 0##, ##C = D = 1/2##) is the max violation of conservation of angular momentum per the PR case. To get the corresponding result for the Mermin photon state, simply replace the last PR joint probability in analogous fashion, again with ##\theta = \pi##. In that case, the PR joint probabilities violate conservation of angular momentum with total anti-correlation while the Mermin photon state satisfies conservation of angular momentum with total correlation. Thus, we have a spectrum of superquantum correlations all violating conservation of angular momentum.
So, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a ‘causal influence’ or hidden variables acting on a trial-by-trial basis to account for that conservation. That is the essence of a “principle theory.” Indeed, the kinematic structure (Minkowski spacetime) of special relativity and the kinematic structure (qubit Hilbert space) of quantum mechanics both follow from NPRF, so we now know that quantum mechanics is on par with special relativity as a principle theory (again, see this Insight).
Therefore, my answer to QIT’s version of Wheeler’s question is
The Tsirelson bound obtains because of conservation per no preferred reference frame.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation per NPRF [16,17,18]) to dispel the mystery of entanglement and answer Wheeler’s question depends on whether or not you can accept the fundamentality of a principle explanation via patterns in both space and time (see this Insight). While we have a compelling 4D constraint (who would argue with conservation per NPRF?) for our adynamical explanation, we do not have a compelling dynamical counterpart. That is, we do not have a consensus, causal mechanism to explain outcomes on a trial-by-trial basis when the SG magnets/polarizers are not co-aligned, and we cannot use counterfactual definiteness per classical probability theory to account for the fact that we conserve angular momentum on average. So, perhaps we do not need new physics to rise to Wilczek’s challenge [19].
To me, ascending from the ant’s-eye view to the God’s-eye view of physical reality is the most profound challenge for fundamental physics in the next 100 years.
[Note: “God’s-eye view” simply means the blockworld, block universe, “all-at-once”, or 4D view like that of Minkowski spacetime, there is no religious connotation.] Since special relativity already supports that view, perhaps we should accept that adynamical explanation is fundamental to dynamical explanation, so that not all adynamical explanations have dynamical counterparts [20]. In that case, “we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?” [1]
References
- Wheeler, J.A.: How Come the Quantum?, New Techniques and Ideas in Quantum Measurement Theory 480(1), 304–316 (1986).
- Cirel’son, B.S.: Quantum Generalizations of Bell’s Inequality, Letters in Mathematical Physics 4, 93–100 (1980).
- Landau, L.J.: On the violation of Bell’s inequality in quantum theory, Physics Letters A 120(2), 54–56 (1987).
- Khalfin, L.A., and Tsirelson, B.S.: Quantum/Classical Correspondence in the Light of Bell’s Inequalities, Foundations of Physics 22(7), 879–948 (1992).
- Mermin, N.D.: Bringing home the atomic world: Quantum mysteries for anybody, American Journal of Physics 49(10), 940–943 (1981).
- Bohm, D.: Quantum Theory, Prentice-Hall, New Jersey (1952).
- La Rosa, A.: Introduction to Quantum Mechanics, Chapter 12
- Dehlinger, D., and Mitchell, M.W.: Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory, American Journal of Physics 70(9), 903–910 (2002).
- Bell, J.: On the Einstein-Podolsky-Rosen paradox, Physics 1, 195–200 (1964).
- Garg, A., and Mermin, N.D.: Bell Inequalities with a Range of Violation that Does Not Diminish as the Spin Becomes Arbitrarily Large, Physical Review Letters 49(13), 901–904 (1982).
- Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
- Bub, J.: Bananaworld: Quantum Mechanics for Primates, Oxford University Press, Oxford, UK (2016).
- Bub, J.: Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B, 241–266 (2004).
- Bub, J.: Why the Tsirelson bound?, in The Probable and the Improbable: The Meaning and Role of Probability in Physics, eds. Meir Hemmo and Yemima Ben-Menahem, Springer, Dordrecht, 167–185 (2012).
- Weinberg, S.: The Trouble with Quantum Mechanics (2017).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Kohler, I: Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum, Entropy 21(7), 692 (2019).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D.: Answering Mermin’s challenge with conservation per no preferred reference frame, Scientific Reports 10, 15771 (2020).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s, Entropy 23(1), 114 (2021).
- Wilczek, F.: Physics in 100 Years, Physics Today 69(4), 32–39 (2016).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford University Press, Oxford, UK (2018).
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018) and “Einstein’s Entanglement” (Oxford UP, 2024).


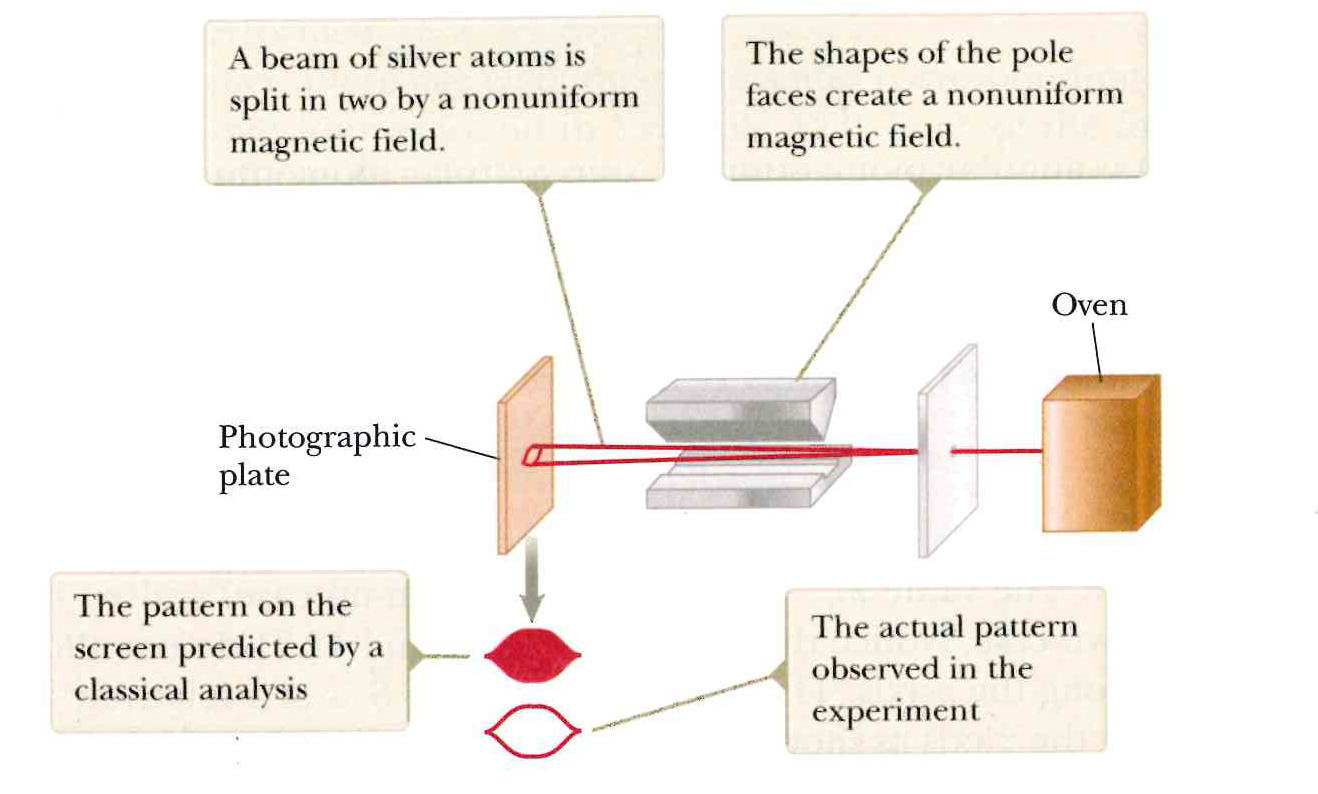 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.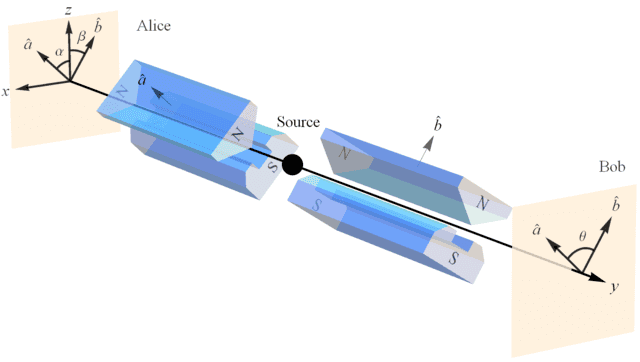








Of course QM produces the quantum correlation function. How else should I reproduce them? The very point of Bell's ingeneous work was to show that local deterministic HV theories can't reproduce the correlations. So what's the goal of your investigation? Is it to find a non-local deterministic model/theory?
I'll try to read your preprint, but still it is clear that angular-momentum conservation holds exactly and it's the very reason for the spin entanglement in this setup used to perform the Bell experiment. It's not only conserved on average!Does whatever form of conservation you're referring too for different settings reproduce the quantum correlation function without using QM? That's what Unnikrishnan's conservation principle does.
I'll try to read your preprint, but still it is clear that angular-momentum conservation holds exactly and it's the very reason for the spin entanglement in this setup used to perform the Bell experiment. It's not only conserved on average!
I used Unnikrishnan's conservation principle to explain the Mermin device in this paper. It's written at the level of Am. J. Phys. (where it's under review), so you should be able to follow it if you've had an introductory course in physics.
Nothing nonsensical like that has to be postulated "as the basis for QM correlations". Everything is within the well-established formalism of standard QT. I still seem not to get what's "the hype" about whichever "amazing coincidence". All you need to understand the measured "QM correlations" is standard QT, where entanglement is common. In the 21st century entanglement shouldn't be puzzling to anybody anymore since it's a well-established empirical fact to describe the corresponding correlations right.This paper https://arxiv.org/pdf/1703.11003.pdf might help you accept the proposed conservation principle as reasonable. He doesn't invoke the conservation principle at all, but he sets it up using single-particle measurements. In fact, he could avoid his conclusion
the exhortation that “correlations cry out for explanation” is one that was learned in the context of a different kind of (classical) physical thinking and therefore not appropriate in a discussion of quantum entanglement.if he would take his reasoning one step further as Unnikrishnan did.
Nothing nonsensical like that has to be postulated "as the basis for QM correlations". Everything is within the well-established formalism of standard QT. I still seem not to get what's "the hype" about whichever "amazing coincidence". All you need to understand the measured "QM correlations" is standard QT, where entanglement is common. In the 21st century entanglement shouldn't be puzzling to anybody anymore since it's a well-established empirical fact to describe the corresponding correlations right.So, if that conservation principle is "nonsensical," then the fact that it reproduces the QM correlations is just an amazing coincidence.
Nothing nonsensical like that has to be postulated "as the basis for QM correlations". Everything is within the well-established formalism of standard QT. I still seem not to get what's "the hype" about whichever "amazing coincidence". All you need to understand the measured "QM correlations" is standard QT, where entanglement is common. In the 21st century entanglement shouldn't be puzzling to anybody anymore since it's a well-established empirical fact to describe the corresponding correlations right.
Sigh. I seem not to be able to make this obvious point. It doesn't make sense to measure the components of the single-particle spins in different directions and then claim that you don't have strict conservation of angular momentum. The algebra of vectors implies that adding vectors is component by component and not components of different directions. Even in classical physics although the total angular momentum of two particles is 0, in general ##J_{1x}+J_{1y} neq 0##. So this has nothing to do with quantum mechanics but it's simply a statement about angular-momentum conservation which doesn't make any sense!You’re absolutely correct when you say that this type of conservation isn’t necessarily related to QM. That’s why it has to be postulated as the basis for QM correlations. That’s why I asked if you thought it was just an amazing coincidence that it reproduces the QM correlations. So, one last time, which do you believe?
Sigh. I seem not to be able to make this obvious point. It doesn't make sense to measure the components of the single-particle spins in different directions and then claim that you don't have strict conservation of angular momentum. The algebra of vectors implies that adding vectors is component by component and not components of different directions. Even in classical physics although the total angular momentum of two particles is 0, in general ##J_{1x}+J_{1y} neq 0##. So this has nothing to do with quantum mechanics but it's simply a statement about angular-momentum conservation which doesn't make any sense!
But you explain yourself correctly what happens for measurements in different directions. However, what's puzzling with that? It's a pretty simple calculation, and that there are correlations, even those violating Bell's inequality and other correlation measures contradicting the assumption of deterministic local models, is the very point of doing such "Bell-test experiments". This expresses a deep fact of Nature, but it doesn't imply that angular-momentum conservation is valid only on average. In fact in this case it's precisely valid on an event-by-event basis. This is the very point of the connection between conservation laws and entanglement. You yourself explain this in the first part of your Insights article!When the measurements are not co-aligned, there is no way to get strict conservation for any given trial, it can only obtain on average. The assumption of conservation of this type is independent of QM (as Unnikrishnan explains), so it could just be a coincidence that it yields the QM correlations.
But you explain yourself correctly what happens for measurements in different directions. However, what's puzzling with that? It's a pretty simple calculation, and that there are correlations, even those violating Bell's inequality and other correlation measures contradicting the assumption of deterministic local models, is the very point of doing such "Bell-test experiments". This expresses a deep fact of Nature, but it doesn't imply that angular-momentum conservation is valid only on average. In fact in this case it's precisely valid on an event-by-event basis. This is the very point of the connection between conservation laws and entanglement. You yourself explain this in the first part of your Insights article!
I read the first part of your Insights article again, i.e., the part which discusses QT, and I don't see any contradiction between what you state there with standard quantum theory, and it is precisely the statement I made in #361 concerning event-by-event conservation of angular momentum for the spin-singlet state (of course for what you call "Mermin photon state" the arguments are analogous). Of course, precise event-by-event angular-momentum conservation in the there explained sense (i.e., in both my postings and also in your Insight in the paragraph directly after the figure showing the SG experiment) holds both within QT and in all experiments done so far at high accuracy and significance. That's all I wanted to say about it.
What I don't understand is, what precisely do you consider a puzzle or "an amazing coincidence".You keep ignoring the situation when Alice and Bob do different measurements, the co-aligned case is trivial. The significance of the result is how conservation obtains for different measurements, as Unnikrishnan showed and I explain in the Insight. That such average, frame-independent conservation yields exactly the QM correlation is either expressing a deep fact of Nature or it is just an amazing coincidence.
I read the first part of your Insights article again, i.e., the part which discusses QT, and I don't see any contradiction between what you state there with standard quantum theory, and it is precisely the statement I made in #361 concerning event-by-event conservation of angular momentum for the spin-singlet state (of course for what you call "Mermin photon state" the arguments are analogous). Of course, precise event-by-event angular-momentum conservation in the there explained sense (i.e., in both my postings and also in your Insight in the paragraph directly after the figure showing the SG experiment) holds both within QT and in all experiments done so far at high accuracy and significance. That's all I wanted to say about it.
What I don't understand is, what precisely do you consider a puzzle or "an amazing coincidence".
And I told you that this is not the right interpretation of conservation of a vector-like quantity. It means that the three components of this quantity are conserved, and this is indeed the case for the spin-singlet two-particle state discussed. It doesn't make sense to measure the spin component of one of the particles and another spin component of the other when you talk about conservation of angular momentum (on an event-by-event basis or (only) on average).
It was a historically very important finding by Bothe et al that the conservation laws hold on an event-by-event basis (in this historic case it was verified for Compton scattering using the coincidence method, for which Bothe received a Nobel prize for very good reasons).
What do you mean by "spatiotemporal pattern of outcomes per conservation of angular momentum". What's done to verify angular-momentum conservation is just what I said previously: You measure the components of the angular momentum for both particles always in the same direction, and given the preparation in the angular-momentum-zero state (in the center-momentum frame that's indeed the spin-zero state) of the pair, these components are precisely back to back, i.e., adding to 0, and this is what is usually defined as conservation of angular momentum.
Already in classical physics it doesn't make sense to measure the components of a conserved quantitiy in different directions for subsystems and then claime the total vector is not conserved, because these components don't add up to the initial total vector quantity. It doesn't even make geometrical nor physical sense to add vector components in different directions.Again, either the result is correct (i.e., conservation as explained in the Insight and published by Unnikrishnan) or it is just an amazing coincidence. You seem to be waffling between those two positions.
And I told you that this is not the right interpretation of conservation of a vector-like quantity. It means that the three components of this quantity are conserved, and this is indeed the case for the spin-singlet two-particle state discussed. It doesn't make sense to measure the spin component of one of the particles and another spin component of the other when you talk about conservation of angular momentum (on an event-by-event basis or (only) on average).
It was a historically very important finding by Bothe et al that the conservation laws hold on an event-by-event basis (in this historic case it was verified for Compton scattering using the coincidence method, for which Bothe received a Nobel prize for very good reasons).
What do you mean by "spatiotemporal pattern of outcomes per conservation of angular momentum". What's done to verify angular-momentum conservation is just what I said previously: You measure the components of the angular momentum for both particles always in the same direction, and given the preparation in the angular-momentum-zero state (in the center-momentum frame that's indeed the spin-zero state) of the pair, these components are precisely back to back, i.e., adding to 0, and this is what is usually defined as conservation of angular momentum.
Already in classical physics it doesn't make sense to measure the components of a conserved quantitiy in different directions for subsystems and then claime the total vector is not conserved, because these components don't add up to the initial total vector quantity. It doesn't even make geometrical nor physical sense to add vector components in different directions.
What is the "4D constraint"? As I already said, in this case angular momentum is, according to standard QT, not only on average conserved but strictly for each individual particle pair!
There's no need for new theories if the old ones perfectly work fine. Since QT is causal, as any physical theory must be, there's also no argument against QT from this corner. Many people find QT unsatisfactory, because it's not deterministic. Well, physics is not there to please people's opinions about how Nature should work but it tries to figure out as accurately as one can how Nature in fact works.
Whether there is a deterministic HV theory consistent with all knows facts, I don't know. If there is one, it will be as puzzling as QT since it's for sure non-local, as is shown by the violation of Bell's inequality, and a non-local theory that's consistent with the relativistic space-time structure, will be very mind-boggling. Maybe it's not even possible to construct such a model, but this one cannot rule out yet.As we've all been telling you, the only way to get conservation when the measurements are different is on average. That means the conservation principle applies not only between spatially separated outcomes but also between temporally separated pairs of outcomes, i.e., 4D. Hidden variables and 'causal mechanisms' are not required, QM is simply describing the spatiotemporal (4D) pattern of outcomes per conservation of angular momentum.
That might have been the reason for Einstein, but……To my mind, Einstein didn't want to accept that "quantum probabilities" are – so to speak – irreducible. In his book “Quantum Reality – Beyond the New Physics” Nick Herbert drops the term “quantum ignorance”:
“Once you get down to the quantum randomness level, no further explanation is possible. You can’t go any deeper because physics stops here. Albert Einstein, no fan of the orthodox ontology, objected to this fundamental lawlessness at the heart of nature when he said that he could not believe that God would play dice with the universe. This new kind of ultimate indeterminism may be called quantum ignorance: we don’t know why an electron strikes a particular phosphor because there’s nothing there to know about. When the dice fall from the cup, on the other hand, their unpredictable outcome is caused by classical ignorance — by our unavoidably partial knowledge of their real situation.”
Many people find QT unsatisfactory, because it's not deterministic.That might have been the reason for Einstein, but that is not an accurate explanation for why everyone finds QT to be unsatisfactory. I would say that the measurement problem is the reason most people find the minimal interpretation of QT unsatisfactory.
Of course, but here the minimal interpretation again solves this apparent quibble. The state with its probabilistic meaning refers to an ensemble. To empirically check, whether angular momentum is conserved, you prepare an ensemble and for each member you measure the spin components of both particles in the same direction. Then you'll find with 100% probability (i.e., for each event) a sum of 0, i.e., angular momentum in this direction is conserved. You can repeat the measurement as often as you like in an arbitrary direction.That doesn't address the issue of what statistics you get when you measure one particle of a twin pair along one axis and you measure the other particle along a different axis.
Of course, the quantum state implies more statistical properties than that, namely the correlations for measurements of spin components of the two particles in different directions, among them choices, where Bell's inequality is predicted (and empirically found with high significance for e.g., polarization-entangled photon pairs) to be violated, disproving the possibility of local deterministic hidden-variable models.The point of the Insights article was to try to derive the statistics for measurements in arbitrary directions without assuming the Born rule, and without assuming the mathematics of spin states.
So, it sounds like you're happy to accept the 4D constraint (conservation on average) as a sufficient explanation of Bell-inequality-violating QM correlations. No need to look for hidden variables or 'causal mechanisms'. In that case, we're in agreement.What is the "4D constraint"? As I already said, in this case angular momentum is, according to standard QT, not only on average conserved but strictly for each individual particle pair!
There's no need for new theories if the old ones perfectly work fine. Since QT is causal, as any physical theory must be, there's also no argument against QT from this corner. Many people find QT unsatisfactory, because it's not deterministic. Well, physics is not there to please people's opinions about how Nature should work but it tries to figure out as accurately as one can how Nature in fact works.
Whether there is a deterministic HV theory consistent with all knows facts, I don't know. If there is one, it will be as puzzling as QT since it's for sure non-local, as is shown by the violation of Bell's inequality, and a non-local theory that's consistent with the relativistic space-time structure, will be very mind-boggling. Maybe it's not even possible to construct such a model, but this one cannot rule out yet.
But in the case where you measure spins along different axes, it's not possible for the vectorial sum of the two measured angular momenta to be zero exactly.Of course, but here the minimal interpretation again solves this apparent quibble. The state with its probabilistic meaning refers to an ensemble. To empirically check, whether angular momentum is conserved, you prepare an ensemble and for each member you measure the spin components of both particles in the same direction. Then you'll find with 100% probability (i.e., for each event) a sum of 0, i.e., angular momentum in this direction is conserved. You can repeat the measurement as often as you like in an arbitrary direction.
Of course, the quantum state implies more statistical properties than that, namely the correlations for measurements of spin components of the two particles in different directions, among them choices, where Bell's inequality is predicted (and empirically found with high significance for e.g., polarization-entangled photon pairs) to be violated, disproving the possibility of local deterministic hidden-variable models.
No, he simply has proven that theories obeying the "realism postulate of EPR" and Bell's inequalities are not compatible with precise angular-momentum conservation, as is predicted by QT. As far as I know, so far nobody has ever found the fundamental conservation laws violated in any quantum experiment. So I choose to use QT describing the empirical facts rather than using a theory obeying a strange notion of "realism" a la EPR, which is disproven by the Bell experiments with overwhelming significance.So, it sounds like you're happy to accept the 4D constraint (conservation on average) as a sufficient explanation of Bell-inequality-violating QM correlations. No need to look for hidden variables or 'causal mechanisms'. In that case, we're in agreement.
Both you and Unnikrishnan show that the correlation functions for QM and the conservation laws, P(a.b,)[SUB]QM[/SUB] = P(a,b,)[SUB]C[/SUB] = – a.b. = – cosθ.
How is superposition of entangled spin 1/2 particles 1/2 (|ud} – |du}) and photons 1/2 (|H}[SUB]1[/SUB] |V}[SUB]2[/SUB] ± |V}[SUB]1[/SUB]H}[SUB]2[/SUB])
in accord with conservation laws in the context of the question by @ftr above in post #345 ?Sorry, I haven't been able to keep up with the discussion lately. If I understand your question correctly (and that in #345), the QM conservation at work here is different than in classical mechanics (CM). I tried to explain in the Insight and in other posts here, so I won't repeat all that. The major difference is that in CM there is a "true" value for the angular momentum ##vec{L}## for each of the two particles and Alice and Bob measure some component (and therefore fraction) of ##vec{L}## for their respective particles. In QM what Alice and Bob measure is always +1 or -1, no fractions. That means they have conservation of angular momentum only on average (unless they choose to measure along the same direction in which case they get exact cancelation). Of course, as pointed out by ftr, that leaves a mystery for the person who wants to know what makes the particles behave properly on a trial-by-trial basis, i.e., there is no hidden variable or 'causal mechanism' to account for conservation on average. So, this conservation principle leaves a mystery for those who demand dynamical explanation. That's the point of the Insight. Are you happy with the 4D constraint (conservation on average) as the fundamental explanation? Or, do you demand a dynamical/causal explanation? As with the many examples in my blockworld series, dynamical thinking creates a mystery that is resolved by blockworld constraint-based thinking.
Fine, I've no problems with that. It only doesn't mean that angular momentum isn't conserved exactly on an "event-by-event basis". It was a very old error by Kramers and Bohr to assume that the conservation laws only hold on average. It was ingeniouly disproven by Walther Bothe with his coincidence measurement method (here applied to Compton scattering). He got the Nobel prize for this method.But in the case where you measure spins along different axes, it's not possible for the vectorial sum of the two measured angular momenta to be zero exactly.
Then you believe Unnikrishnan's result is a mere coincidence? That's a pretty amazing coincidence, but you are free to believe that!No, he simply has proven that theories obeying the "realism postulate of EPR" and Bell's inequalities are not compatible with precise angular-momentum conservation, as is predicted by QT. As far as I know, so far nobody has ever found the fundamental conservation laws violated in any quantum experiment. So I choose to use QT describing the empirical facts rather than using a theory obeying a strange notion of "realism" a la EPR, which is disproven by the Bell experiments with overwhelming significance.
The whole point of the article is to derive the probabilities for measurements in different directions.Fine, I've no problems with that. It only doesn't mean that angular momentum isn't conserved exactly on an "event-by-event basis". It was a very old error by Kramers and Bohr to assume that the conservation laws only hold on average. It was ingeniouly disproven by Walther Bothe with his coincidence measurement method (here applied to Compton scattering). He got the Nobel prize for this method.
The result generalizes to the conservation of anything represented by a Bell basis state, as we show in the corresponding paper https://arxiv.org/abs/1807.09115. Unnikrishnan showed likewise. In his own wordsBoth you and Unnikrishnan show that the correlation functions for QM and the conservation laws, P(a.b,)[SUB]QM[/SUB] = P(a,b,)[SUB]C[/SUB] = – a.b. = – cosθ.
How is superposition of entangled spin 1/2 particles 1/2 (|ud} – |du}) and photons 1/2 (|H}[SUB]1[/SUB] |V}[SUB]2[/SUB] ± |V}[SUB]1[/SUB]H}[SUB]2[/SUB])
in accord with conservation laws in the context of the question by @ftr above in post #345 ?
Well, that's why I was asking whether the derivation of quantum probabilities extended to things other than spin.The result generalizes to the conservation of anything represented by a Bell basis state, as we show in the corresponding paper https://arxiv.org/abs/1807.09115. Unnikrishnan showed likewise. In his own words The results I proved are the following: Assuming the conservations laws are valid over the ensemble and the observables are discreet valued, there is unique correlation function independent of the nature of the theory. This coincides with what we derive from quantum mechanics. Any correlation function that deviates from this violates conservation laws. Local hidden variable theories are in this class, since all of them have a different correlation (not only less, but linear functions, at lest in parts ). Thus, Bell's inequalities deals with unphysical theories and are redundant. Testing the inequalities is naive physics, akin to trying to build perpetual machines. The result that deviation marks unphysical theories applies both ways. The correlation is exactly what is predicted by conservation laws, not less, not more. Given a state, conservation law over ensemble gives the quantum correlation. For mixed state correlation can approach classical correlation, but obeying the conservation laws (the correlation reduced only because there is a mixture of angular momentum states – by classically averaging over the mixture you can get the correct quantum correlation.).
https://arxiv.org/pdf/quant-ph/0407041.pdf
These authors believe so.
@RUTA
Does your Frame independent conservation apply in this paper and how soI'm presenting his result and cited the published version of that paper in my Insight:
10. Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
I've been in correspondence with him and he would say "perspective invariance" rather than "no preferred reference frame." Essentially, I'm using his result to answer a question in the QIT community, "Why the Tsirelson bound?" The frame independence approach is in response to QIT's desire to answer their question a la the light postulate of SR. It is supremely ironic that Unnikrishnan's result can be used to answer QIT's question precisely per their desideratum while Unnikrishnan himself does not subscribe to "no preferred reference frame." In another twist, Unnikrishnan doesn't believe Bell's paper should be related to the EPR paper at all. So, right now I'm trying to convince him to let me use his result to answer their question anyway. We'll see.
I think we've discussed this already. The only thing QT tells you in this state is that if you measure the components of the electron and the positron in the same direction you get always opposite results since the total angular momentum is of course 0. This is what it means that anglar momentum is precisely conserved for any single event. If you measure the components in different direction you have only probabilities, as it must be in view of the uncertainty relation for angular-momentum components in different directions.Then you believe Unnikrishnan's result is a mere coincidence? That's a pretty amazing coincidence, but you are free to believe that!
My elementary understanding is that conservation law is not enough, since both particles are in superposition of up and down before measurement. So conservation law makes it even more mysterious if anything, as if both particles are linked all the time. Am I saying this wrong.
If you measure the components in different direction you have only probabilities, as it must be in view of the uncertainty relation for angular-momentum components in different directions.The whole point of the article is to derive the probabilities for measurements in different directions.
Conservation of angular momentum gives rise to that Bell basis state, yes, but how do the actual measurement outcomes along any direction conform to conservation of angular momentum? Only on average, as I explain. This should come as no surprise, since we know QM gives rise to CM on average. The only surprise is that QM's version of conservation is very different from CM in that it requires no 'causal mechanism' or hidden variables. Indeed, after decades of argument, one could reasonably conclude that QM conservation is not compatible with a 'causal mechanism' or hidden variables. But, I'm sure dBB advocates would not agree :-)I think we've discussed this already. The only thing QT tells you in this state is that if you measure the components of the electron and the positron in the same direction you get always opposite results since the total angular momentum is of course 0. This is what it means that anglar momentum is precisely conserved for any single event. If you measure the components in different direction you have only probabilities, as it must be in view of the uncertainty relation for angular-momentum components in different directions.
So, after such a long thread, does conservation of angular momentum solve the the ERP or not, as the claim is in OP?https://arxiv.org/pdf/quant-ph/0407041.pdf
These authors believe so.
@RUTA
Does your Frame independent conservation apply in this paper and how so
My understanding is that EPR is not limited to spin. Also position is not discrete.Well, that's why I was asking whether the derivation of quantum probabilities extended to things other than spin.
In the usual most simple setup of the EPR argument by Bohm angular momentum is precisely zero and not only on average.Did you read the article?
I've no clue what you mean by that the Born rule is the "weirdest part of the Born interpretation".Oh, well. I don't know how to help you, there.
hay everyone this is way to complicated natural things are simple
In the usual most simple setup of the EPR argument by Bohm angular momentum is precisely zero and not only on average. The most simple example is to take neutral pions in their rest frame and then look at the (rare) cases, where the pion decays to an electron-positronium pair. The total angular momentum of the pair is precisely 0 for each such decay and not only on average. The spin state is the singlet state
$$|Psi rangle=frac{1}{sqrt{2}} (|1/2,-1/2 rangle – |-1/2,1/2 rangle).$$Conservation of angular momentum gives rise to that Bell basis state, yes, but how do the actual measurement outcomes along any direction conform to conservation of angular momentum? Only on average, as I explain. This should come as no surprise, since we know QM gives rise to CM on average. The only surprise is that QM's version of conservation is very different from CM in that it requires no 'causal mechanism' or hidden variables. Indeed, after decades of argument, one could reasonably conclude that QM conservation is not compatible with a 'causal mechanism' or hidden variables. But, I'm sure dBB advocates would not agree :-)
So, after such a long thread, does conservation of angular momentum solve the the ERP or not, as the claim is in OP? My understanding is that EPR is not limited to spin. Also position is not discrete.The Bell basis states giving rise to the Tsirelson bound could in principle represent conservation other than angular momentum, as stated in the arXiv version of the paper https://arxiv.org/abs/1807.09115. Now, does conservation per no preferred reference frame, as explained in the paper/Insight, resolve the mystery of EPR-Bell?
Well, that depends on what you require for "explanation" in this case. If you need a 'causal mechanism' or hidden variables to explain the QM correlations violating Bell's inequality, then the answer is "conservation per no preferred reference frame does not resolve the mystery of EPR-Bell." Conservation per no preferred reference frame is different than conservation in classical mechanics (CM). In CM for conservation of angular momentum, you would have two opposing angular momentum vectors (one for Alice's particle and one for Bob's particle) canceling out. Bob and Alice would be free to measure the angular momentum of their particles along any direction they liked, thereby measuring something less than the magnitude in general. In that situation, the direction along which the two angular momentum vectors were anti-aligned would be a "hidden variable" and constitute a "preferred direction in space" for that particular trial (see my post #33). In an entangled quantum exchange of momentum, Bob and Alice always measure +1 or -1, never any fractions. And, both can say their measurement directions and outcomes were "right" while the other person's measurement outcomes along their directions were only "right" on average. That kind of "frame-independent conservation" constitutes a deep explanation of the QM correlations violating Bell's inequality … for me, anyway.
So, for me, the constraint (conservation per no preferred reference frame) is compelling enough that I don't require any additional 'causal mechanisms' or hidden variables to explain the constraint. In CM, of course, you can explain the conservation of angular momentum dynamically — it occurs when the net torque on the system is zero. But, apparently, in QM no further explanation for the constraint is required (or even possible), the constraint itself is (necessarily) the "last word." [The use of constraints rather than dynamical laws as fundamental explanans throughout physics is the leitmotif of our book, "Beyond the Dynamical Universe." So, I'm very biased :-)]
As we elaborate in the paper, the light postulate (LP) of SR is an excellent analogy. There, time dilation and length contraction both follow from the fact that "the speed of light c is the same in all reference frames." At the time Einstein postulated it, everyone was looking to explain the LP, not use it to explain other things. The LP was a mystery itself, so many people did not accept the use of one mystery to explain others. Likewise, the frame-independent manner of QM conservation is itself a profound mystery for many people. So, for those people, it cannot be used to explain the QM correlations violating Bell's inequality.
I don't think there was a claim that it "solves" it, but that the quantum correlations for EPR can be derived by assuming:
It's sort of interesting, because the weirdest part of the Born interpretation—that you square the amplitude to get the probability–is not assumed.
But I don't think it actually solves the conceptual puzzles with EPR.
I also wonder whether the derivation can be generalized to show that the Born rule, in general, is implied by conservation laws plus discreteness?In the usual most simple setup of the EPR argument by Bohm angular momentum is precisely zero and not only on average. The most simple example is to take neutral pions in their rest frame and then look at the (rare) cases, where the pion decays to an electron-positronium pair. The total angular momentum of the pair is precisely 0 for each such decay and not only on average. The spin state is the singlet state
$$|Psi rangle=frac{1}{sqrt{2}} (|1/2,-1/2 rangle – |-1/2,1/2 rangle).$$
I've no clue what you mean by that the Born rule is the "weirdest part of the Born interpretation". There's nothing weird about it at all. It defines the meaning of the quantum state in a concise and simple way.
My understanding is that EPR is not limited to spin. Also position is not discrete.
So, after such a long thread, does conservation of angular momentum solve the the ERP or not, as the claim is in OP?I don't think there was a claim that it "solves" it, but that the quantum correlations for EPR can be derived by assuming:
It's sort of interesting, because the weirdest part of the Born interpretation—that you square the amplitude to get the probability–is not assumed.
But I don't think it actually solves the conceptual puzzles with EPR.
I also wonder whether the derivation can be generalized to show that the Born rule, in general, is implied by conservation laws plus discreteness?
So, after such a long thread, does conservation of angular momentum solve the the ERP or not, as the claim is in OP?
Concerning the question of interpretation, Weinberg's book "Lectures on Quantum Mechanics" is even better although I don't agree with his conclusion that there's something unsolved concerning QM and measurements.The unsolved problem is the measurement problem in the sense of this post:
after the observer has chosen the device (by whatever rule), there remains the pure quantum problem to show that the device actually produces on each reading the numbers that qualify as a measurement, in the sense that they satisfy Born's rule.
This is the measurement problem! It has nothing to do with the observer but is a purely quantum mechanical problem.namely to show how given the unitary evolution of the system measured plus detector plus environment, the detector actually produces on each reading the numbers that qualify as a measurement.
You write,
Ok, that's true. Of course, it's only possible for very simple cases in a strict way (like the famous analysis of tracks of charged particles in vapour chambers by Mott or the measurement of spin components in the Stern Geralach experiment).But your statement is not quite true, since these analyses assume Born's rule for measurements and hence assume what is to be demonstrated.
The problem is solved for some special case in the papers by Allahverdian et al., but as discussed here, these make assumptions different from the tradition.
I don't understand what you mean.Maybe because I wrote "no certainty" instead of "no uncertainty" ?(fixed now)
Let me introduce one more step: after the interaction of the electron with the SG apparatus we have a superposition of a state where it flies to the left with spin up and a state where it flies to the right with spin down. If you put a screen as a measurement device to right, you either get a blob or you don't. Getting a blob corresponds to the electron travelling to the right with spin down, not getting a blob corresponds to the electron travelling to the left with spin up.That is crystal clear.
So only after looking for the presence of the blob, the observer can say anything definite about the spin.I don't have to look at the blob after preparation. It is sufficient to look at the latest screen, because no electron measure there can be there without having gone trough the left path. I don't see how it is not strictly equivalent to looking at the blob.
Beside, there is even a temporal relationship between electron measure "to be present" even before the first S/G (preparation) and the electron at the final screen result. Electron can be emitted in the beam one per day for example…
By "carefully distinguish" I mean a tangible discussion of both types of situations: an experiment, where the observer actually gets multiple outcomes and an experiment, where state reduction is used for convenience because certain parts of the state aren't relevant for future measurements. And ideally also how one can modify an experiment such that it falls into the other class.Yes, I've never seen that explicitly discussed in a textbook. I think I realized it sometime after reading LL (which is the first book from which I understood quantum mechanics because of its explicit mention of the classical measuring apparatus), and not just the formal postulates. It also helped by explicitly seeing how this is played out in the indirect measurements formalism with a quantum ancilla, and showing that the reduced density matrix is the same as that after a projective measurement in which information about the result is not retained. However, I still did not know it in every specific situation. For example, I did not know about the unitary description of a polarizer until @Cthugha pointed it out to me here on PF many years after I had already learnt QM.
What passage exactly do you have in mind? In his 2005 paper, he talks about the possibility of "subjective definiteness" so his notion of "definite outcome" seems to be more general to me.Nothing so specific, just his general term "definite outcome", eg. https://arxiv.org/abs/quant-ph/0312059 has a whole section II.B headed "The problem of definite outcomes".
BTW, I realized my memory of LL was faulty, and even they do not state the idea of an "irreversible macroscopic outcome" so clearly. It must be something I picked up with their help.
The concept of irreversibility is mentioned more clearly in Haag's 1996 "Local Quantum Physics" on p304: "In Bohr's discussion the time asymmetry appears as obvious. For instance: "The irreversible amplification effects on which the registration of the existence of atomic objects depends reminds us of the essential irreversibility inherent in the very concept of observation" [Bohr 58]."
Landau and Lifshitz does. They are careful to say that a measurement produces an irreversible macroscopic mark, […]By "carefully distinguish" I mean a tangible discussion of both types of situations: an experiment, where the observer actually gets multiple outcomes and an experiment, where state reduction is used for convenience because certain parts of the state aren't relevant for future measurements. And ideally also how one can modify an experiment such that it falls into the other class.
which is nowadays often called a "definite outcome" following Schlosshauer's influential review.What passage exactly do you have in mind? In his 2004 paper, he talks about the possibility of "subjective definiteness" so his notion of "definite outcome" seems to be more general to me.
In any case, I think that the word "outcome" should be avoided if one doesn't speak about the perception of a person. It is loaded language which blurrs the boundary between what is independent of the observer and what isnt.
Not again this wrong statement. You cannot admit at the same time that the classical behavior is derivable from QT and then claim that there is a cut. That's a contradictio in adjecto!OK, let's try this again, since we seem to agree on the error in section 9.5 of Ballentine's book. Here is LL stating explicitly that classical concepts are needed in the formulation of QM postulates, and that it is also true that classical mechanics is a limit of quantum mechanics. Here are some relevant quotes from p2-3 of the English translation.
"A more general theory can usually be formulated in a logically complete manner, independent of a less general theory which forms a limiting case of it. … It is in principle impossible, however, to formulate the basic concepts of quantum mechanics without using classical mechanics."
"By measurement, in quantum mechanics, we understand any process of interaction between classical and quantum objects …."
"Thus quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case, yet at the same time it requires this limiting case for its own formulation."
I don't like the equation of measurement with state reduction or terminology like "a measurement has occurred". State reduction neither fully captures what happens in a measurement (it leaves out the outcome) nor is it exclusively used for measurements (it's also used for convenience in situations where the observer doesn't obtain any knowledge).That's true. For the purposes of the interpretation of quantum mechanics, I think what's important is not measurement, specifically, but interactions that cause a microscopic quantity to become correlated with the results of an irreversible macroscopic change. Such interactions are not actually measurements, because we might not actually learn anything from them.
For modeling purposes, one of these examples of interactions leading to decoherence and macroscopic entanglement can often be thought of as a measurement followed by forgetting the result of the measurement. That sounds like that combination should be the same as doing nothing, but it isn't, in combination with the Born rules.
But the preparation consist of taking only the electron from the left path ! Every electron used after that first "preparating" "Left of Stern Gerlach" is one of those… There is no certainty there, isn't it ? What am I missing that is so obvious for you physicists ?I don't understand what you mean. Let me introduce one more step: after the interaction of the electron with the SG apparatus we have a superposition of a state where it flies to the left with spin up and a state where it flies to the right with spin down. If you put a screen as a measurement device to right, you either get a blob or you don't. Getting a blob corresponds to the electron travelling to the right with spin down, not getting a blob corresponds to the electron travelling to the left with spin up. So only after looking for the presence of the blob, the observer can say anything definite about the spin.
I don't see anything confusing or incorrect on page 5, 6. What do you mean exactly?Me neither. There's nothing incorrect on pages 5, 6 in Ballentine's book, where he discusses an SG experiment with neutrons. Also there, however, he doesn't measure the spin components before recombining the "partial beams", i.e., there's no decoherence and that's why the recombination leads back to the original state.
Nevertheless, Ballentine is among the best QM textbooks I know of.
Concerning the question of interpretation, Weinberg's book "Lectures on Quantum Mechanics" is even better although I don't agree with his conclusion that there's something unsolved concerning QM and measurements. What's unsolved is the lack of a consistent quantum description of the gravitational field, but it's not measurement within standard QM and QFT, where the great success of QT describing the empirical findings shows that in fact there's no problem from the point of view of physics. Maybe there's a puzzle for philosophers about reality and such things, but that's philosophy, not physics.
I don't see anything confusing or incorrect on page 5, 6. What do you mean exactly?Ballentine is not confusing me – atyy is !
Because of "if the electron arrives there". You don't know if it will arrive to the right or to the left. Only after the measurement to the right has been performed do you know that it arrived there.But the preparation consist of taking only the electron from the left path ! Every electron used after that first "preparating" "Left of Stern Gerlach" is one of those… There is no certainty there, isn't it ? What am I missing that is so obvious for you physicists ?
Yet if you perform a measurement located somewhere to the right of the SG apparatus, you know that if the electron arrives there, it definitely has spin up. This is why it is sensible to call this a preparation for this measurement.But what I cannot got trough my thick skull (or sick, go figure), is how that differs in any shape of form from the very definition of "measurement".Because of "if the electron arrives there". You don't know if it will arrive to the right or to the left. Only after the measurement to the right has been performed do you know that it arrived there.
But in this case he is wrong.I don't dispute this. I just don't have access to the book right now and can't comment on the specifics of where I think he went wrong.
I have no suggestion about "correct" terminology, however I see no contradiction between the idea that SG apparatus changes the spin state of particle and the fact that two beams can be recombined in a way that restores original spin state.
In order to observe interference we have to preserve relative phase between spin modes and have to make it matter by recombining beams. And interference is responsible for restoration of the original spin state.
If relative phase plays no role in later manipulations we of course can drop spatially separate part of the beam from description by projection.
Production of measurement record necessarily destroys any relative phase relationship as in this process the system interacts with one or more particles which are necessarily removed from experimental setup and do not participate in any later manipulations. But then it has little to do with spin or any other property of the particle (except position of course as we place detectors at certain spot).An SG apparatus without a screen to detect the two partial beams of the silver atom can, however, be seen as a preparation procedure for definite spin states, i.e., you get an entanglement between position and spin component in direction of the magnetic field (with theoretically arbitrary accuracy), i.e., an atom at one of the clearly distinguished places of the two partial beams has a determined spin component ##pm hbar/2##. The wave function (a Weyl spinor) is
$$Psi(x)=psi_+(x) |hbar/2 rangle + psi_{-}(x) |-hbar/2 rangle,$$
where the ##psi_{pm}## have (FAPP) no overlap.
At this point, however, the spin component has not yet been measured, i.e., to know the spin component of a single atom that run through the magnet you have to register at which position it ends up at a screen or something equivalent. Only then you have done a measurement, and this measurement will distroy the relative phase between the two partial beams, which occur in the superposition written above for ##Psi##. After such a measurement a "recombination" of the two partial beams in the sense Ballentine writes in his book is not possible anymore. This is due to the decoherence that necessarily occurs through the interaction of the atom with the measurement apparatus.
Step 3 is different because there's also the screen which allows the experimenter to make an observation.OK the screen is a different apparatus. There is only one screen, and it is after step4. I recognize that. The screen interact with the position observable.
If you have only a single electron and use a Stern Gerlach apparatus to put it in a superposition of flying to the right with spin up and flying to the left with spin down you cannot say anything definite about its spin.Of course, if there is not "spacial/position" screening…. and there is only one electron…
So you shouldn't call this a measurement.OK fine, I'll not call it a measurement, even though every single one of the electron are known to have been prepared/picked up from the left beam. Which seem to me to be identical to having put a screen with a hole only on the left path.
Yet if you perform a measurement located somewhere to the right of the SG apparatus, you know that if the electron arrives there, it definitely has spin up. This is why it is sensible to call this a preparation for this measurement.But what I cannot got trough my thick skull (or sick, go figure), is how this differs in any shape of form from the very definition of "measurement".
Listen I found some resource with similar setup that seems to be analysed in detail. I'll read it ten time over and eventually get back to you.
Thank you
To see that the separation by itself is not a measurement, I could redirect both streams back together into a single stream, and then no measurement of spin would ever be performed.I have no suggestion about "correct" terminology, however I see no contradiction between the idea that SG apparatus changes the spin state of particle and the fact that two beams can be recombined in a way that restores original spin state.
In order to observe interference we have to preserve relative phase between spin modes and have to make it matter by recombining beams. And interference is responsible for restoration of the original spin state.
If relative phase plays no role in later manipulations we of course can drop spatially separate part of the beam from description by projection.
Production of measurement record necessarily destroys any relative phase relationship as in this process the system interacts with one or more particles which are necessarily removed from experimental setup and do not participate in any later manipulations. But then it has little to do with spin or any other property of the particle (except position of course as we place detectors at certain spot).
What he shows there is that in this case there cannot be a state reduction. Exactly as described by stevendarryl. Do you disagree with that?Ballentine indeed does show that in his setup there's no state reduction. The only problem with this argument is that even a proponent of the collapse hyposis wouldn't claim that a state reduction has happend since in this setup the spin components at points B and C are not measured.
I agree that he strawmans Copenhagen. But to be fair, I don't know any textbook which carefully distinguishes situations without intermediate outcomes from real sequential measurements off the top of my head.But in this case he is wrong. A measurement means that you have let the system interact with an apparatus with outcomes for pointers that are in one-to-one correspondence with the value of the measured observable (I don't talk about incomplete measurements here; that's another interesting story of quite recent research on what measurement means in quantum theory), but this is not the case in the neutron interferometer experiment described in Ballentines book.
Well, you could say that the notion of "compatible" is state-dependent. For spin, for example, we have:
##[S_i, S_j] = i varepsilon_{ijk} S_k##
If compatible means that the commutator is zero, then ##S_i## and ##S_j## are compatible when all components of spin are zero.Usually one defines observables as compatible only when their representing operators commute, i.e., when there exists a complete set of orthonormalized simultaneous eigenvectors.
So you claim.What he shows there is that in this case there cannot be a state reduction. Exactly as described by stevendarryl. Do you disagree with that?
I agree that he strawmans Copenhagen. But to be fair, I don't know any textbook which carefully distinguishes situations without intermediate outcomes from real sequential measurements off the top of my head.Landau and Lifshitz does. They are careful to say that a measurement produces an irreversible macroscopic mark, which is nowadays often called a "definite outcome" following Schlosshauer's influential review.
This is indeed one of the errors in Ballentine – he claims that Copenhagen must treat this as a collapse even when no definite outcome is obtained.I agree that he strawmans Copenhagen. But to be fair, I don't know any textbook which carefully distinguishes situations without intermediate outcomes from real sequential measurements off the top of my head.
So you shouldn't call this a measurement.Actually, I did use the term like this myself in the past. My usage of the term "measurement" has considerably evolved over the time and now I think that the best way to speak of it is simply the everyday language: a measurement is the action of a person to obtain knowledge about a part of the world. A neccessary condition for a device to act as a measurement device is that said person can read out the measurement outcome. This leads to certain requirements about the physical interaction between the device and the system of interest.
I don't like the equation of measurement with state reduction or terminology like "a measurement has occurred". State reduction neither fully captures what happens in a measurement (it leaves out the outcome) nor is it exclusively used for measurements (it's also used for convenience in situations where the observer doesn't obtain any knowledge).
Well, and what's in your opinion wrong with this section?
I must say, you have indeed a point here, since no spin component is measured at points B and C, and thus even if I assume a collapse in measurements I don't expect any to occur here.Yes, what you said is what is wrong about that section.
I don't see how that supports what you claimed earlier! There is nothing erroneous in that section, and he doesn't say anything aboutCopenhagen.So you claim.
Section 9.5 of the 1998 edition which purports to show the quantum state is not subject to any state reductionI don't see how that supports what you claimed earlier! There is nothing erroneous in that section, and he doesn't say anything aboutCopenhagen.
The setup #269 seems pretty clear. There are 3 identical Stern-Gerlach "apparatus". Yet the step1 is call a "preparer" the step2 a "interaction/useless" the step3 a "measurer".Step 3 is different because there's also the screen which allows the experimenter to make an observation.
I cannot fathom why on earth preparing +X is not a measurement to +X.If you have only a single electron and use a Stern Gerlach apparatus to put it in a superposition of flying to the right with spin up and flying to the left with spin down you cannot say anything definite about its spin. So you shouldn't call this a measurement. Yet if you perform a measurement located somewhere to the right of the SG apparatus, you know that if the electron arrives there, it definitely has spin up. This is why it is sensible to call this a preparation for this measurement.
If you prepare a spin in ##s=0## the components ##vec{n} cdot vec{sigma}## are determined to be 0 for any direction ##vec{n}##. It's the most simple example that sometimes in fact you can prepare special states where incompatible observables are all determined at once.Well, you could say that the notion of "compatible" is state-dependent. For spin, for example, we have:
##[S_i, S_j] = i varepsilon_{ijk} S_k##
If compatible means that the commutator is zero, then ##S_i## and ##S_j## are compatible when all components of spin are zero.
Well, and what's in your opinion wrong with this section?
I must say, you have indeed a point here, since no spin component is measured at points B and C, and thus even if I assume a collapse in measurements I don't expect any to occur here.
The book is over 600 pages, can you be more specific with the citation.Section 9.5 of the 1998 edition which purports to show the quantum state is not subject to any state reduction
If you prepare a spin in ##s=0## the components ##vec{n} cdot vec{sigma}## are determined to be 0 for any direction ##vec{n}##. It's the most simple example that sometimes in fact you can prepare special states where incompatible observables are all determined at once.
To make a spin-entangled electron-positron pair one way is to use a neutral pion which (however rarely) can decay into a single electron-positron pair with total spin 0.0 along which axis ? Otherwise said, is it possible to prepare pion by measuring their spin along some angle, and will it affect the prediction you can make on the spin of the e/p pair ?
Likewise, is putting a polarizer on the incident photon before the crystal, modifying the setup in any measurable way ?
A related question, is that in both cases what is the mathematical relationship for the spin conservation ? I mean the spin must change, because the axis of travel split in two (and thus differ by some angle)
I don't know what you mean. I would have guessed that "information about the previous state" would cover "the electrons have spin-up in the x-direction". That information has not been lost.
Perhaps all measurements are preparations, but the issue is whether all preparations are measurements.For sure not. If I absorb a photon to detect it, this photon is gone. It's not prepared in anything but it's simply not there anymore. Almost all measurements we can do with quantum systems are not preparations. That's another very simple argument why the idea of state collapse in some flavors of Copenhagen is flawed and not relevant for real-world experiments in the lab anyway.