Why the Quantum | A Response to Wheeler’s 1986 Paper
Wheeler’s opening statement in his 1986 paper, “How Come the Quantum?” holds as true today as it did then [1]
The necessity of the quantum in the construction of existence: out of what deeper requirement does it arise? Behind it all is surely an idea so simple, so beautiful, so compelling that when — in a decade, a century, or a millennium — we grasp it, we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?
In this Insight, I will answer Wheeler’s question per its counterpart in quantum information theory (QIT), “How come the Tsirelson bound?” Let me start by explaining the Tsirelson bound and its relationship to the Bell inequality, then it will be obvious what that has to do with Wheeler’s question, “How Come the Quantum?” The answer (the Tsirelson bound is a consequence of conservation per no preferred reference frame (NPRF)) may surprise you with its apparent simplicity, but that simplicity belies a profound mystery, as we will see.
The Tsirelson bound is the spread in the Clauser-Horne-Shimony-Holt (CHSH) quantity
\begin{equation}\langle a,b \rangle + \langle a,b^\prime \rangle + \langle a^\prime,b \rangle – \langle a^\prime,b^\prime \rangle \label{CHSH1}\end{equation}
created by quantum correlations. Here, we consider a pair of entangled particles (or “quantum systems” or “quantum exchanges of momentum”). Alice makes measurements on one of the two particles with her measuring device set to ##a## or ##a^\prime## while Bob makes measurements on the other of the two particles with his measuring device set to ##b## or ##b^\prime##. There are two possible outcomes for either Bob or Alice in either of their two possible settings given by ##i## and ##j##. For measurements at ##a## and ##b## we have for the average of Alice’s results multiplied by Bob’s results on a trial-by-trial basis
\begin{equation}\langle a,b \rangle = \sum (i \cdot j) \cdot P(i,j \mid a,b) \label{average}\end{equation}
That’s a bit vague, so let me supply some actual physics. The two entangled states I will use are those which uniquely give rise to the Tsirelson bound [2-4] , i.e., the spin singlet state and the ‘Mermin photon state’ [5]. The spin singlet state is ##\frac{1}{\sqrt{2}} \left(\mid ud \rangle – \mid du \rangle \right)## where ##u##/##d## means the outcome is displaced upwards/downwards relative to the north-south pole alignment of the Stern-Gerlach (SG) magnets (Figure 1).
 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
This state obtains due to conservation of angular momentum at the source as represented by momentum exchange in the spatial plane P orthogonal to the source collimation (“up or down” transverse). This state might be produced by the dissociation of a spin-zero diatomic molecule [6] or the decay of a neutral pi meson into an electron-positron pair [7], processes which conserve spin angular momentum. For more information about the spin singlet state and the spin triplet states, see this Insight.
The Mermin state for photons is ##\frac{1}{\sqrt{2}} \left(\mid VV \rangle + \mid HH \rangle \right)## where ##V## means the there is an outcome (photon detection) behind one of the coaligned polarizers and ##H## means there is no outcome behind one of the co-aligned polarizers. This state obtains due to conservation of angular momentum at the source as represented by momentum exchange along the source collimation (“yes” or “no” longitudinal). Dehlinger and Mitchell created this state by laser inducing spontaneous parametric downconversion in beta barium borate crystals [8], a process that conserves spin angular momentum as represented by the polarization of the emitted photons. At this point we will focus the discussion on the spin single state for total anti-correlation, since everything said of that state can be easily transferred to the Mermin photon state.
Let us investigate what Alice and Bob discover about these entangled states in the various contexts of their measurements (Figure 2). Alice’s detector responds up and down with equal frequency regardless of the orientation ##\alpha## of her SG magnet. This is in agreement with the relativity principle, aka “no preferred reference frame” (NPRF), where different SG magnet orientations relative to the source constitute different “reference frames” in quantum mechanics just as different velocities relative to the source constitute different “reference frames” in special relativity (see this Insight).
Figure 2. Alice and Bob making spin measurements in the xz plane on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors.
Bob observes the same regarding his SG magnet orientation ##\beta##. Thus, the source is rotationally invariant in the spatial plane P orthogonal to the source collimation. When Bob and Alice compare their outcomes, they find that their outcomes are perfectly anti-correlated (##ud## and ##du## with equal frequency) when ##\alpha – \beta = \theta = 0## (Figure 3). This is consistent with conservation of angular momentum per classical mechanics between the pair of detection events (again, this fact defines the state). The degree of that anti-correlation diminishes as ##\theta \rightarrow \frac{\pi}{2}## until it is equal to the degree of correlation (##uu## and ##dd##) when their SG magnets are at right angles to each other. In other words, whenever the SG magnets are orthogonal to each other anti-correlated and correlated outcomes occur with equal frequency, i.e., conservation of angular momentum in one direction is independent of the angular momentum changes in any orthogonal direction. Thus, we wouldn’t expect to see more correlation or more anti-correlation based on conservation of angular momentum for transverse results in the plane P when the SG magnets are orthogonal to each other. As we continue to increase the angle ##\theta## beyond ##\frac{\pi}{2}## the anti-correlations continue to diminish until we have totally correlated outcomes when the SG magnets are anti-aligned. This is also consistent with conservation of angular momentum, since the totally correlated results when the SG magnets are anti-aligned represent momentum exchanges in opposite directions in the plane P just as when the SG magnets are aligned, it is now simply the case that what Alice calls up, Bob calls down and vice-versa.
The counterpart for the Mermin photon state is simply that angular momentum conservation is evidenced by ##VV## or ##HH## outcomes for coaligned polarizers. When the polarizers are at right angles you have only ##VH## and ##HV## outcomes, which is still totally consistent with conservation of angular momentum as ‘not ##H##’ implies ##V## and vice-versa [8]. In other words, a polarizer does not have a ‘north-south’ distinction (longitudinal rather than transverse momentum exchange). In particular, having rotated either or both polarizers by ##\pi## one should obtain precisely ##VV## or ##HH## outcomes again.
Nothing is particularly mysterious about the entangled states for electron spin or photon polarization described here so far because we have been thinking as if conservation of angular momentum holds for each experimental trial, as in classical mechanics. Truth is, since Alice and Bob can only measure +1 or -1 (quantum exchange of momentum per NPRF), we can only get conservation of angular momentum in any particular trial when their SG magnets/polarizers are co-aligned. And, we cannot use classical probability theory to account for the conservation of angular momentum on average.
In particular, the probability that Alice and Bob will measure ##uu## or ##dd## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityuu}\end{equation}
And, the probability that Alice and Bob will measure ##ud## or ##du## at angles ##\alpha## and ##\beta## for the spin singlet state is
\begin{equation}P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) \label{probabilityud}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##u##) and -1 (##d##) gives Eq. (\ref{CHSH1}) of
\begin{equation}-\cos(a – b) -\cos(a – b^\prime) -\cos(a^\prime – b) +\cos(a^\prime – b^\prime) \label{CHSHspin}\end{equation}
Choosing ##a = \pi/4##, ##a^\prime = -\pi/4##, ##b = 0##, and ##b^\prime = \pi/2## minimizes Eq. (\ref{CHSHspin}) at ##-2\sqrt{2}## (the Tsirelson bound).
Likewise, for the Mermin photon state we have
\begin{equation}P_{VV} = P_{HH} = \frac{1}{2} \mbox{cos}^2 \left(\alpha – \beta \right) \label{probabilityVV}\end{equation}
and
\begin{equation}P_{VH} = P_{HV} = \frac{1}{2} \mbox{sin}^2 \left(\alpha – \beta \right) \label{probabilityVH}\end{equation}
Using these in Eq. (\ref{average}) where the outcomes are +1 (##V##) and -1 (##H##) gives Eq. (\ref{CHSH1}) of
\begin{equation}\cos2(a – b) +\cos2(a – b^\prime) +\cos2(a^\prime – b) -\cos2(a^\prime – b^\prime) \label{CHSHmermin}\end{equation}
Using ##a = \pi/8##, ##a^\prime = -\pi/8##, ##b = 0##, and ##b^\prime = \pi/4## maximizes Eq. (\ref{CHSHmermin}) at ##2\sqrt{2}## (the Tsirelson bound). So, we have two mysteries.
First, as explained by Mermin [5], suppose you restrict Alice and Bob’s measurement angles ##\alpha## and ##\beta## to three possibilities, setting 1 is ##0^o##, setting two is ##120^o##, and setting three is ##-120^o##. Eq. (\ref{probabilityud}) says the probability of getting opposite results is 1 when ##\alpha = \beta## (1/2 ##ud## and 1/2 ##du##) and 1/4 otherwise (1/8 ##ud## and 1/8 ##du##). Now, if the source emits particles with definite properties that account for their outcomes in the three possible measurement settings, and we have to get total anti-correlation for like settings, then the particles’ so-called “instruction sets” must be opposite for each of the three settings. For example, suppose we have 1(##u##)2(##u##)3(##d##) for Alice and 1(##d##)2(##d##)3(##u##) for Bob. That guarantees the total anti-correlation for like settings, i.e., 11 gives ##ud##, 22 gives ##ud##, and 33 gives ##du##. And, for unlike settings we get anti-correlation in two combinations, i.e., 12 gives ##ud## and 21 gives ##ud##. In fact, for any instruction set with two ##u## and one ##d## we get anti-correlation for unlike settings in two of the six possible unlike combinations (12,13,21,23,31,32). The only other way to make a pair of instruction sets is to have one with all ##u## and the other with all ##d##. In that case, we get anti-correlation for all six unlike combinations. That means the instruction sets necessary to guarantee anti-correlation for like settings lead to an overall anti-correlation greater than 2/6 for unlike settings, which is greater than the quantum probability for anti-correlation in unlike settings of 1/4. This is Mermin’s version of the Bell inequality [9] (fraction of anti-correlated outcomes for unlike settings must be greater than 2/6) and the manner by which it is violated by quantum correlations (1/4 is less than 2/6). Thus, instruction sets (“counterfactual definiteness”) assumed by classical probability theory cannot account for quantum correlations in this case.
The counterpart to this for the CHSH quantity is that classical correlations give a range of -2 to 2 for the CHSH quantity (“CHSH-Bell inequality”). And, as we saw above, the Tsirelson bound violates the CHSH-Bell inequality. Experiments show that the quantum results can be achieved (violating the Bell inequality), ruling out an explanation of these correlated momentum exchanges via instruction sets per classical probability theory.
The second mystery is that even in cases where we don’t violate the Bell inequality, e.g., ##a = b = 0## and ##a^\prime = b^\prime = \pi/2## which give a CHSH value of 0, we still have conservation of angular momentum. Why is that mysterious? Well, it’s not when the SG magnets are co-aligned, since in those cases we always get a +1 outcome and a -1 outcome for a total of zero. But, in trials where ##\alpha – \beta = \theta## does not equal zero, we need either Alice or Bob, at minimum, to measure something less than 1 to conserve angular momentum. For example, if Alice measures +1, then Bob must measure ##-\cos{\theta}## to conserve angular momentum for that trial. But, again, Alice and Bob only measure +1 or -1 (quantum exchange of momentum per NPRF, which uniquely distinguishes the quantum joint distribution from its classical counterpart [10]), so that can’t happen (Figure 4). What does happen? We conserve angular momentum on average in those trials.
It is easy to see how this follows by starting with total angular momentum of zero for binary (quantum) outcomes +1 and -1 (I am suppressing the factor of ##\hbar/2## and I’m referring to the spin singlet state here [11], Figure 3).

Figure 3. Outcomes (yellow dots) in the same reference frame, i.e., outcomes for the same measurement (blue arrows represent SG magnet orientations), for the spin singlet state explicitly conserve angular momentum.
Alice and Bob both measure +1 and -1 results with equal frequency for any SG magnet angle (NPRF) and when their angles are equal they obtain different outcomes giving total angular momentum of zero. The case (a) result is not difficult to understand via conservation of angular momentum, because Alice and Bob’s measured values of spin angular momentum cancel directly when ##\alpha = \beta##, that defines the spin singlet state. But, when Bob’s SG magnet is rotated by ##\alpha – \beta = \theta## relative to Alice’s, the situation is not as clear (Figure 6).
In classical physics, one would say the projection of the angular momentum vector of Alice’s particle ##\vec{S}_A = +1\hat{a}## along ##\hat{b}## is ##\vec{S}_A\cdot\hat{b} = +\cos{(\theta)}## where again ##\theta## is the angle between the unit vectors ##\hat{a}## and ##\hat{b}## (Figure 2). From Alice’s perspective, had Bob measured at the same angle, i.e., ##\beta = \alpha##, he would have found the angular momentum vector of his particle was ##\vec{S}_B = -1\hat{a}##, so that ##\vec{S}_A + \vec{S}_B = \vec{S}_{Total} = 0##. Since he did not measure the angular momentum of his particle at the same angle, he should have obtained a fraction of the length of ##\vec{S}_B##, i.e., ##\vec{S}_B\cdot\hat{b} = -1\hat{a}\cdot\hat{b} = -\cos{(\theta)}## (Figure 4).

Figure 4. The projection of the angular momentum of Bob’s particle ##\vec{S}_B## along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum due to NPRF.
Of course, Bob only ever obtains +1 or -1 per NPRF, so Bob’s outcomes can only average the required ##-\cos{(\theta)}##. Thus, NPRF dictates
\begin{align*}
P_{uu} + P_{ud} & = \frac {1}{2} \\
P_{ud} + P_{dd} & = \frac {1}{2},
\end{align*}
These equations now allow us to uniquely solve for the joint probabilities
\begin{equation}
P_{uu} = P_{dd} = \frac{1}{2} \mbox{sin}^2 \left(\frac{\theta}{2} \right) \label{QMjointLike}
\end{equation}
and
\begin{equation}
P_{ud} = P_{du} = \frac{1}{2} \mbox{cos}^2 \left(\frac{\theta}{2} \right) \label{QMjointUnlike}
\end{equation}
\begin{equation}
\overline{BA-} = 2P_{du}(+1) + 2P_{dd}(-1) = \cos (\theta) \label{BA-}
\end{equation}
Using Eqs. (\ref{BA+}) and (\ref{BA-}) in Eq. (\ref{consCorrel}) we obtain
\begin{equation}
\langle \alpha,\beta \rangle = \frac{1}{2}(+1)_A(-\mbox{cos} \left(\theta\right)) + \frac{1}{2}(-1)_A(\mbox{cos} \left(\theta\right)) = -\mbox{cos} \left(\theta\right) \label{consCorrel2}
\end{equation}
which is precisely the correlation function for a spin singlet state found using the joint probabilities per quantum mechanics. To see that we simply use Eqs. (\ref{probabilityuu}) and (\ref{probabilityud}) in Eq. (\ref{average}) to get
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)(-1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(+1)\frac{1}{2} \mbox{cos}^2 \left(\frac{\alpha – \beta}{2}\right) +\\ &(+1)(+1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) + (-1)(-1)\frac{1}{2} \mbox{sin}^2 \left(\frac{\alpha – \beta}{2}\right) \\ &= -\mbox{cos} \left(\alpha – \beta \right) = -\mbox{cos} \left(\theta \right)
\end{split}
\label{correl}\end{equation}
Thus, “average-only” conservation maps beautifully to our classical expectation (Figures 6 & 7). Since the angle between SG magnets ##\theta## is twice the angle between Hilbert space measurement bases, this result easily generalizes to conservation per NPRF of whatever the measurement outcomes represent when unlike outcomes entail conservation in the symmetry plane [15] (see this Insight on the Bell spin states). However, again, none of the formalism of quantum mechanics is used in obtaining Eq. (\ref{consCorrel2}) or our quantum state Eqs. (\ref{QMjointLike}) & (\ref{QMjointUnlike}). In deriving the quantum correlation function and quantum state in this fashion, we assumed only NPRF.For the Mermin photon state, conservation of angular momentum is established by ##V## (designated by +1) and ##H## (designated by -1) results through a polarizer. When the polarizers are co-aligned Alice and Bob get the same results, half pass and half no pass. Thus, conservation of angular momentum is established by the intensity of the electromagnetic radiation applied to binary outcomes for various polarizer orientations. As with spin angular momentum, this is classical thinking applied to binary outcomes per conservation of angular momentum. Again, grouping Alice’s results into +1 and -1 outcomes we see that she would expect to find ##[\mbox{cos}^2\theta – \mbox{sin}^2\theta]## at ##\theta## for her +1 results and ##[\mbox{sin}^2\theta – \mbox{cos}^2\theta]## for her -1 results. Since Bob measures the same thing as Alice for conservation of angular momentum, those are Bob’s averages when his polarizer deviates from Alice’s by ##\theta##. Therefore, the correlation of results for conservation of angular momentum is given by
\begin{equation}\langle \alpha,\beta \rangle =\frac{(+1_A)(\mbox{cos}^2\theta – \mbox{sin}^2\theta)}{2} + \frac{(-1_A)(\mbox{sin}^2\theta – \mbox{cos}^2\theta)}{2} = \cos{2\theta} \label{merminconserve}\end{equation}
which is precisely the correlation given by quantum mechanics.As before, we need to find ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## so we need four independent conditions. Normalization and ##P_{VH} = P_{HV}## are the same as for the spin case. The correlation function
\begin{equation}
\begin{split}
\langle \alpha,\beta \rangle = &(+1)_A(+1)_BP_{VV} + (+1)_A(-1)_BP_{VH} + \\&(-1)_A(+1)_BP_{HV} + (-1)_A(-1)_BP_{HH}\label{correlFn2}
\end{split}
\end{equation}
along with our conservation principle represented by Eq. (\ref{merminconserve}) give
\begin{equation}
P_{VV} – P_{VH} = -\frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
and
\begin{equation}
P_{HV} – P_{HH} = \frac{1}{2}(\mbox{sin}^2\theta – \mbox{cos}^2\theta)
\end{equation}
Solving these four equations for ##P_{VV}##, ##P_{HH}##, ##P_{VH}##, and ##P_{HV}## gives precisely Eqs. (\ref{probabilityVV}) & (\ref{probabilityVH}).Notice that since the angle between polarizers ##\alpha – \beta## equals the angle between Hilbert space measurement bases, this result immediately generalizes to conservation per NPRF of whatever the outcomes represent when like outcomes entail conservation in the symmetry plane [15] (again, see this Insight on the Bell spin states).Since the quantum correlations violate the Bell inequality to the Tsirelson bound and satisfy conservation per NPRF while the classical correlations do not violate the Bell inequality, the classical correlations do not satisfy conservation per NPRF. Experiments of course tell us that Nature obeys the quantum correlations and therefore the conservation per NPRF.

Figure 5. A spatiotemporal ensemble of 8 experimental trials for the Bell spin states showing Bob’s outcomes corresponding to Alice‘s ##+1## outcomes when ##\theta = 60^\circ##. Angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{60^\circ}=\frac{1}{2}##). It is impossible for angular momentum to be conserved explicitly in each trial since the measurement outcomes are binary (quantum) with values of ##+1## (up) or ##-1## (down) per no preferred reference frame. The conservation principle at work here assumes Alice and Bob’s measured values of angular momentum are not mere components of some hidden angular momentum with variable magnitude. That is, the measured values of angular momentum are the angular momenta contributing to this conservation.
Figure 6. For the spin singlet state (S = 0). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from –1 (totally down, arrow bottom) to 0 to +1 (totally up, arrow tip). This obtains per conservation of angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of angular momentum on average, because they only measure +1/-1, never a fractional result. Thus, just as with the light postulate of special relativity, we see that no preferred reference frame leads to counterintuitive results (see this Insight).
Figure 7. The situation is similar for the spin triplet states where outcomes agree for the same measurement in the plane containing the conserved angular momentum vector (S = 1). Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to –1 (totally down, arrow bottom). This obtains per conservation of angular momentum on average in the plane containing the S = 1 spin angular momentum in accord with no preferred reference frame. See this Insight for details.
So, while conservation per NPRF sounds like a very reasonable constraint on the distribution of quantum exchange of momentum (+1 or -1, no fractions), we still do not have any causal mechanism to explain the outcomes of any particular trial when the SG magnets/polarizers are not co-aligned (Figure 4). And, as I showed above, we cannot use instruction sets per classical probability theory to account for the Tsirelson bound needed to explain the conservation of angular momentum on average. Thus, while we have a very reasonable constraint on the distribution of entangled quantum exchanges (conservation of angular momentum), that constraint has no compelling dynamical counterpart, i.e., no consensus causal mechanism to explain the outcome of any particular trial when the SG magnets/polarizers are not co-aligned and no counterfactual definiteness to explain why conservation of angular momentum is conserved on average. What we have is a “principle” account of entanglement and the Tsirelson bound (see this Insight). I will return to this point after showing how so-called “superquantum correlations” fail to satisfy this constraint as well.
There are QIT correlations that not only violate the Bell inequality, but also violate the Tsirelson bound. Since these correlations violate the Tsirelson bound, they are called “superquantum correlations.” The reason QIT considers these correlations reasonable (no known reason to reject their possibility) is because they do not violate superluminal communication, i.e., the joint probabilities don’t violate the no-signaling condition
\begin{equation}\begin{split}P(A \mid a\phantom{\prime},b\phantom{\prime}) &= P(A \mid a\phantom{\prime}, b^\prime)\\
P(A \mid a^\prime,b\phantom{\prime}) &= P(A \mid a^\prime, b^\prime)\\
P(B \mid a\phantom{\prime},b\phantom{\prime}) &= P(B \mid a^\prime, b\phantom{\prime})\\
P(B \mid a\phantom{\prime},b^\prime) &= P(B \mid a^\prime, b^\prime )\end{split}\label{nosig}\end{equation}
This means Alice and Bob measure the same outcomes regardless of each other’s settings. If this wasn’t true, Alice and Bob would notice changes in the pattern of their outcomes as the other changed their measurement settings. Since the measurements for each trial can be spacelike separated that would entail superluminal communication.
The Popescu-Rohrlich (PR) joint probabilities
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
produce a value of 4 for Eq. (\ref{CHSH1}), the largest of any no-signaling possibilities. Thus, the QIT counterpart to Wheeler’s question, “How Come the Quantum?” is “Why the Tsirelson bound?” [12-14]. In other words, is there any compelling principle that rules out superquantum correlations as conservation of angular momentum ruled out classical correlations? Let us look at Eq. (\ref{PRcorr}) in the context of our spin singlet and Mermin photon states. Again, we will focus the discussion on the spin singlet state and allude to the obvious manner by which the analysis carries over to the Mermin photon state.
The last PR joint probability certainly makes sense if ##a^\prime = b^\prime##, i.e., the total anti-correlation implying conservation of angular momentum, so let us start there. The third PR joint probability makes sense for ##b = \pi + b^\prime##, where we have conservation of angular momentum with Bob having flipped his coordinate directions. Likewise, then, the second PR joint probability makes sense for ##a = \pi + a^\prime##, where we have conservation of angular momentum with Alice having flipped her coordinate directions. All of this is perfectly self consistent with conservation of angular momentum as we described above, since ##a^\prime## and ##b^\prime## are arbitrary per rotational invariance in the plane P. But now, the first PR joint probability is totally at odds with conservation of angular momentum. Both Alice and Bob simply flip their coordinate directions, so we should be right back to the fourth PR joint probability with ##a^\prime \rightarrow a## and ##b^\prime \rightarrow b##. Instead, the first PR joint probability says that we have total correlation (maximal violation of conservation of angular momentum) rather than total anti-correlation per conservation of angular momentum, which violates every other observation. In other words, the set of PR observations violates conservation of angular momentum in a maximal sense. To obtain the corresponding argument for angular momentum conservation per the correlated outcomes of the Mermin photon state, simply start with the first PR joint probability and show the last PR joint probability maximally violates angular momentum conservation.
To find the degree to which superquantum correlations violate our constraint, replace the first PR joint probability with
\begin{equation}\begin{split}&p(1,1 \mid a,b) = C \\
&p(-1,-1 \mid a, b) = D \\
&p(1,-1 \mid a,b) = E \\
&p(-1,1 \mid a, b) = F \\ \end{split} \label{PRcorrMod}\end{equation}
The no-signaling condition Eq. (\ref{nosig}) in conjunction with the second and third PR joint probabilities gives ##C = D## and ##E = F##. That in conjunction with normalization ##C + D + E + F =1## and P(anti-correlation) + P(correlation) = 1 means total anti-correlation (##E = F = 1/2##, ##C = D = 0##) is the conservation of angular momentum per the quantum case while total correlation (##E = F = 0##, ##C = D = 1/2##) is the max violation of conservation of angular momentum per the PR case. To get the corresponding result for the Mermin photon state, simply replace the last PR joint probability in analogous fashion, again with ##\theta = \pi##. In that case, the PR joint probabilities violate conservation of angular momentum with total anti-correlation while the Mermin photon state satisfies conservation of angular momentum with total correlation. Thus, we have a spectrum of superquantum correlations all violating conservation of angular momentum.
So, we see explicitly in this result how quantum mechanics conforms statistically to a conservation principle without need of a ‘causal influence’ or hidden variables acting on a trial-by-trial basis to account for that conservation. That is the essence of a “principle theory.” Indeed, the kinematic structure (Minkowski spacetime) of special relativity and the kinematic structure (qubit Hilbert space) of quantum mechanics both follow from NPRF, so we now know that quantum mechanics is on par with special relativity as a principle theory (again, see this Insight).
Therefore, my answer to QIT’s version of Wheeler’s question is
The Tsirelson bound obtains because of conservation per no preferred reference frame.
Whether or not you consider this apparently simple 4-dimensional (4D) constraint (conservation per NPRF [16,17,18]) to dispel the mystery of entanglement and answer Wheeler’s question depends on whether or not you can accept the fundamentality of a principle explanation via patterns in both space and time (see this Insight). While we have a compelling 4D constraint (who would argue with conservation per NPRF?) for our adynamical explanation, we do not have a compelling dynamical counterpart. That is, we do not have a consensus, causal mechanism to explain outcomes on a trial-by-trial basis when the SG magnets/polarizers are not co-aligned, and we cannot use counterfactual definiteness per classical probability theory to account for the fact that we conserve angular momentum on average. So, perhaps we do not need new physics to rise to Wilczek’s challenge [19].
To me, ascending from the ant’s-eye view to the God’s-eye view of physical reality is the most profound challenge for fundamental physics in the next 100 years.
[Note: “God’s-eye view” simply means the blockworld, block universe, “all-at-once”, or 4D view like that of Minkowski spacetime, there is no religious connotation.] Since special relativity already supports that view, perhaps we should accept that adynamical explanation is fundamental to dynamical explanation, so that not all adynamical explanations have dynamical counterparts [20]. In that case, “we will all say to each other, how could it have been otherwise? How could we have been so stupid for so long?” [1]
References
- Wheeler, J.A.: How Come the Quantum?, New Techniques and Ideas in Quantum Measurement Theory 480(1), 304–316 (1986).
- Cirel’son, B.S.: Quantum Generalizations of Bell’s Inequality, Letters in Mathematical Physics 4, 93–100 (1980).
- Landau, L.J.: On the violation of Bell’s inequality in quantum theory, Physics Letters A 120(2), 54–56 (1987).
- Khalfin, L.A., and Tsirelson, B.S.: Quantum/Classical Correspondence in the Light of Bell’s Inequalities, Foundations of Physics 22(7), 879–948 (1992).
- Mermin, N.D.: Bringing home the atomic world: Quantum mysteries for anybody, American Journal of Physics 49(10), 940–943 (1981).
- Bohm, D.: Quantum Theory, Prentice-Hall, New Jersey (1952).
- La Rosa, A.: Introduction to Quantum Mechanics, Chapter 12
- Dehlinger, D., and Mitchell, M.W.: Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory, American Journal of Physics 70(9), 903–910 (2002).
- Bell, J.: On the Einstein-Podolsky-Rosen paradox, Physics 1, 195–200 (1964).
- Garg, A., and Mermin, N.D.: Bell Inequalities with a Range of Violation that Does Not Diminish as the Spin Becomes Arbitrarily Large, Physical Review Letters 49(13), 901–904 (1982).
- Unnikrishnan, C.S.: Correlation functions, Bell’s inequalities and the fundamental conservation laws, Europhysics Letters 69, 489–495 (2005).
- Bub, J.: Bananaworld: Quantum Mechanics for Primates, Oxford University Press, Oxford, UK (2016).
- Bub, J.: Why the Quantum?, Studies in History and Philosophy of Modern Physics 35B, 241–266 (2004).
- Bub, J.: Why the Tsirelson bound?, in The Probable and the Improbable: The Meaning and Role of Probability in Physics, eds. Meir Hemmo and Yemima Ben-Menahem, Springer, Dordrecht, 167–185 (2012).
- Weinberg, S.: The Trouble with Quantum Mechanics (2017).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Kohler, I: Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum, Entropy 21(7), 692 (2019).
- Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D.: Answering Mermin’s challenge with conservation per no preferred reference frame, Scientific Reports 10, 15771 (2020).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s, Entropy 23(1), 114 (2021).
- Wilczek, F.: Physics in 100 Years, Physics Today 69(4), 32–39 (2016).
- Silberstein, M., Stuckey, W.M., and McDevitt, T.: Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, Oxford University Press, Oxford, UK (2018).
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018).


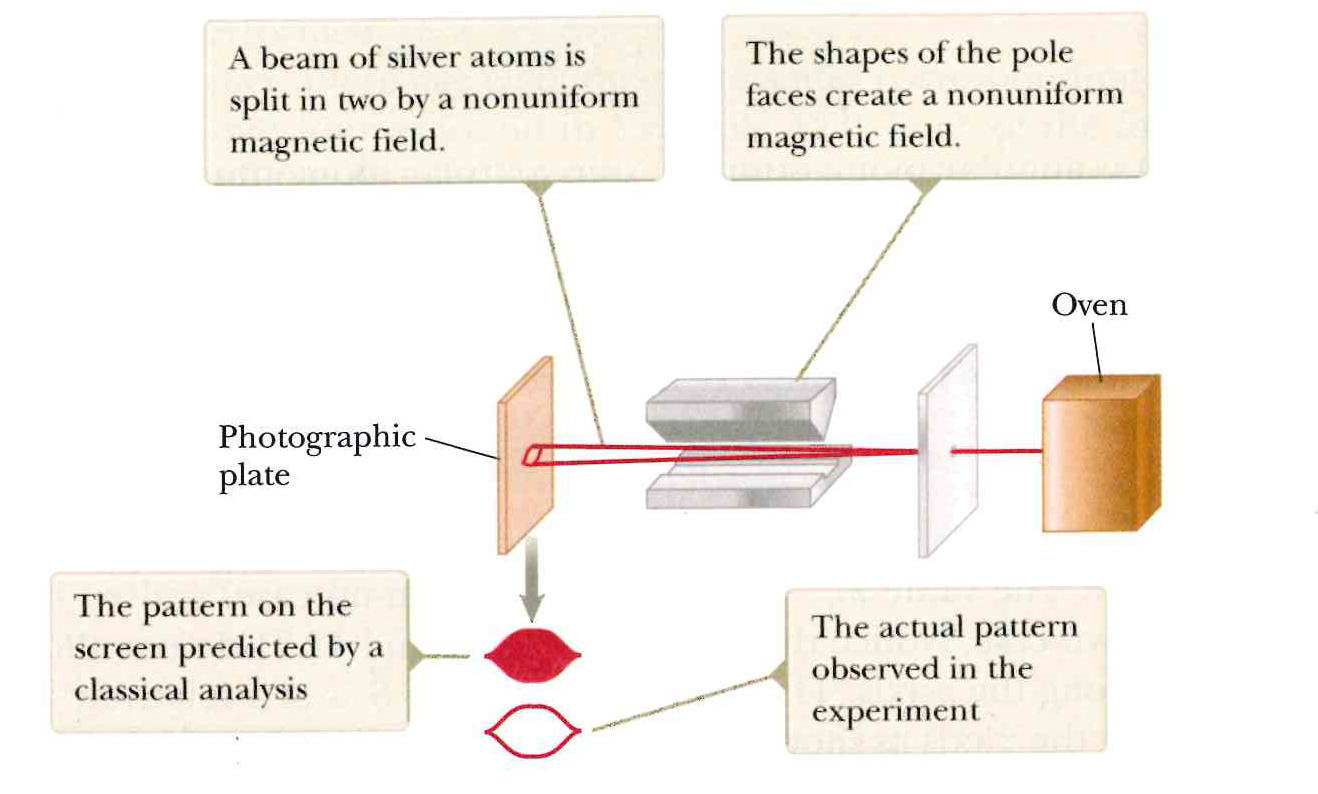 Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up and down, represented numerically by +1 and -1, respectively. Figure 42-16 on page 1315 of Physics for Scientists and Engineers with Modern Physics, 9th ed, by Raymond A. Serway and John W. Jewett, Jr.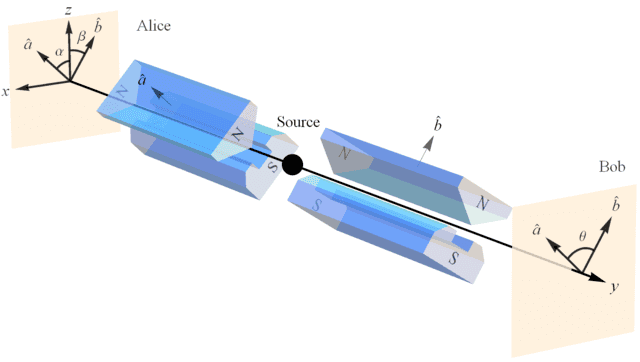








I have not had any advanced physics. However, it is interesting that back in the 1950's, the Popular Science magazine showed a flying craft that was totally silent and could be moved by ionizing air. The only problem was it needed so much power it had to be connected to a power cord coming from a very high energy source. This was well before the use of nuclear capability. It does not seem logical that the United States has not been able to solve the problem of eliminating the restricting cord since then. The speed of such a craft may be another problem.
But you didn't make the point clear! Unnikrishnan does. Even under the assumption of angular-momentum conservation on average, which is less than what's the case for QT, where angular-momentum conservation holds on an event-by-event basis, he can show that there's no local deterministic HV model which leads to the violation of Bell's inequality as predicted by QT. I've not read Mermin's paper, but I don't think it's necessary, because in Unnikrishnan's paper everything is clear.What I had in the paper was just Unnikrishnan's summary paragraph. Obviously, I can't include all the explication he provides in his paper after that summary, but I didn't think it necessary since his summary was very clear to me. Apparently, it wasn't clear to you, so I revised the paper here replacing his summary with my "no preferred reference frame" argument for his conservation of angular momentum on average. My argument is just another way of looking at his argument or just another way of looking at Boughn's argument here. However you justify it, the key insight of Unnikrishnan is to use conservation of angular momentum on average to provide ##overline{BA+}## and ##overline{BA-}## in the correlation function (see post #386). That gives you the quantum correlation function without ever using quantum mechanics. This is akin to deriving the Lorentz transformations from the light postulate (in more ways than one, as I will point out).
As for articulating the fact that Unnikrishnan's result rules out "local HV theories," that's trivially clear from the fact that his conservation principle reproduces the quantum correlation function which rules out local HV theories (I have included that very statement in the paper). In the Mermin paper (had you bothered to read it), he goes to great lengths to explain how his "instruction sets" are the equivalent of any local HV theory. As with the Unnikrishnan paper, I can't include Mermin's entire paper in mine, so I must expect the reader to have read the Mermin paper. The Mermin device is a metaphor for the formalism of QM in this particular experimental set-up. So, when Mermin shows that his device cannot be explained with instruction sets, he's showing how QM rules out local HV theories. The conundrum of the Mermin device is then, "If it doesn't work via instruction sets, how the hell does it work?" Since Unnikrishnan's conservation principle gives the quantum correlation function responsible for the mysterious outcomes of the Mermin device, his conservation principle invoked as a constraint (as with the light postulate) then answers that question, i.e., resolves the conundrum of the Mermin device. However, …
As I point out, Unnikrishnan's conservation principle only resolves the conundrum of the Mermin device if you can accept the conservation principle as a constraint on the distribution of outcomes in space and time with no `deeper mechanism' to account for the constraint proper. In other words, you have to accept the conservation principle as a constraint in and of itself without further explanation. Prima facie the conservation of angular momentum on average sounds like a perfectly reasonable constraint. But, this constraint does not provide a `deeper mechanism' at work on a trial-by-trial basis to account for the average conservation. So someone might still say, "But, what mechanism is responsible for the conservation? How do the particles `know' how to behave in each trial so as to contribute properly to the ensemble? Each particle has `no idea' what the outcomes were at both locations in preceding trials, nor does it `know' what the other device setting is in their particular trial. How the hell does this average conservation pattern in space and time get created?"
And that leads us to the other analogy with the light postulate. Even Michelson of the Michelson-Morley experiment said, "It must be admitted, these experiments are not sufficient to justify the hypothesis of an ether. But then, how can the negative result be explained?" In other words, even Michelson required some `deeper mechanism' to explain why "the speed of light c is the same in all reference frames." In general, if one cannot accept a constraint or postulate in and of itself as the fundamental explanans, that constraint or postulate is just as mysterious as the explanandum. That's the point of my paper and that is the point of our book, "Beyond the Dynamical Universe." So, my paper is just another argument for constraint-based explanation as fundamental to dynamical/causal explanation.
But you didn't make the point clear! Unnikrishnan does. Even under the assumption of angular-momentum conservation on average, which is less than what's the case for QT, where angular-momentum conservation holds on an event-by-event basis, he can show that there's no local deterministic HV model which leads to the violation of Bell's inequality as predicted by QT. I've not read Mermin's paper, but I don't think it's necessary, because in Unnikrishnan's paper everything is clear.
Well, I've just looked up the following paper by Unnikrishnan:
DOI: 10.1209/epl/i2004-10378-y
He got the issue with the conservation law correct, i.e., precisely as I stated several times. Maybe it helps to sharpen also your manuscript if you use his explanation on pages 490 and 491 in his paper, particularly the statement on the conservation law directly under item 2) on page 491. Then it becomes really a non-trivial and interesting issue which sheds further light on Bell's inequality in showing that there's no local deterministic HV theory that obeys the angular-momentum-conservation law on average. This is weaker than to assume the conservation law to be valid for any individual system as is the case for quantum theory for the spin-singlet state.Here is his item 2:
The theory of correlations obeys the conservation of angular momentum on the average over the ensemble, and for the case of singlet state,STotal = 0, there is rotational invariance. Note that this is a weak assumption, since we do not insist on the validity of the conservation law for individual events.He says, immediately thereafter
The second criterion is the main assumption, physically well motivated, in the proof that follows. Since the main assumption is applied only for ensemble averages and not for individual events, I do not make any explicit assumption on locality or reality.That is exactly the point I make when I say Bob can't satisfy conservation of angular momentum on a trial-by-trial basis when he and Alice make measurements at different angles. He can only satisfy the conservation principle an average in such cases. [Of course, he can say the same about Alice.] The correlation function obtained per Unnikrishnan's conservation principle is not satisfied by "instruction sets," which is the Mermin equivalent of saying Unnikrishnan's conservation principle cannot be satisfied by any "local deterministic HV theory." Again, did you read Mermin's paper?
Well, I've just looked up the following paper by Unnikrishnan:
DOI: 10.1209/epl/i2004-10378-y
He got the issue with the conservation law correct, i.e., precisely as I stated several times. Maybe it helps to sharpen also your manuscript if you use his explanation on pages 490 and 491 in his paper, particularly the statement on the conservation law directly under item 2) on page 491. Then it becomes really a non-trivial and interesting issue which sheds further light on Bell's inequality in showing that there's no local deterministic HV theory that obeys the angular-momentum-conservation law on average. This is weaker than to assume the conservation law to be valid for any individual system as is the case for quantum theory for the spin-singlet state.
I haven't missed the point. You have failed to convince me that there is a point. There's nothing non-trivial derived in your paper, and it's written in a way that one has to guess what you want to tell and there's a lot of off-topic ballast in it. Excuse me for being harsh.If you don't understand the conundrum, then you won't appreciate Unnikrishnan's solution and my qualification thereto. I did revise the manuscript according to my efforts to explain it to you, so these exchanges did prove useful :-)
I haven't missed the point. You have failed to convince me that there is a point. There's nothing non-trivial derived in your paper, and it's written in a way that one has to guess what you want to tell and there's a lot of off-topic ballast in it. Excuse me for being harsh.
Again, you've missed the point entirely. Did you even read Mermin's paper? His `Mermin device' produces outcomes he calls "case (a)" and "case (b)." Case (a) outcomes obtain for like settings on his device and case (b) outcomes obtain for unlike settings. The only way he knows to explain the workings of the device in accord with case (a) outcomes, his "instruction sets," is incompatible with the case (b) outcomes, thus the conundrum. You don't need any QM to understand this conundrum, just simple probabilities. He then asks the "physicist reader" to explain how his device works to the "general reader," analogously to how he was able to explain the conundrum of the device to the "general reader." Density matrices, spin operators, and Hilbert space won't cut it. My paper is very close to meeting his challenge. In addition to simple probabilities, which are allowed, I used conservation of angular momentum, which is a bit more. Can you do better? If so, write it up and submit it!
There is no other way today to explain the behavior of matter on the fundamental level than quantum theory. That's the important result of Bell's work on local deterministic hidden-variable theories. There are also no mysteries to be resolved. You only have to accept that there are correlations in quantum physics which cannot be described by such a classical theory but are a natural consequence of quantum theory, named entanglement. These correlations can be "long-ranged", i.e., there can be correlations between properties of distinguishable parts of a quantum system which are very far away.
What's confusing in my point of view is to call this "non-locality". As Einstein already wrote in 1948 (in a paper which is much more to the point than the famous EPR paper which Einstein didn't particularly like so much) the key issue he was uneasy about was the inseparability of quantum systems through the possiblitiy of an entanglement of observables of far-distant parts of a quantum system.
Your example of the spin-entangled spin-singlet state of two-particles is paradigmatic. It's usually easier to realize with polarziation-entangled photon pairs, which nowadays are easily produced through parametric downconversion, but the principle issue is the same. In principle the polarization-entanglement can persist for arbitrary long times (as long as there's no interaction of one of the particles or photons with something else and no decoherence occurs), and thus the particles or photons can be registered by as far distant observers as one likes, and each observer can choose his observable he likes to measure (i.e., in your example which spin component he likes to measure or which polarization state he likes to filter out), but the correlations described through entanglement will be observed.
All this is fully concistent with relativistic local microcausal QFTs. For photons everything is well understood within standard quantum optics, based on QED (with the optical devices treated in hemiclassical approximation, which is of sufficient accuracy for the usual experiments). Since for QED, as for any local QFT, the linked-cluster theorem holds there are "spooky actions at a distance", but the long-ranged "stronger than classically possible" correlations are simply there because of the preparation of the two-particle/two-photon system in an entangled state. Thus although the single-particle spins (resp. single-particle photon polarizations) are maximally indetermined, there's still this strong correlation beween measurement outcomes.
Admittedly this is hard to swallow as long as you don't accept that Nature behaves as she does and doesn't care about our philosophical prejudices due to our everyday experience with macroscopic matter, which behaves pretty classical also according to QT since we don't resolve (and don't need to resolve) every microscopic detail, such that the quantum fluctuations of the corresponding macroscopic coarse-grained obserervables are practically not visible.
In your paper there's nothing explained differently from QT. All you do is to assume the probabilities of QT to be valid and then calculate expectation values due to the rules. That the average of any of the single-particle spin components in any direction is 0 is simply due to the symmetry of the sytem. That's implied by the fact that the total angular momentum is precisely 0 due to the preparation of the particle pair in this state, and this state is a maximally entangled Bell state.
Bell's brillant analysis of this state in terms of a deterministic local theory clearly shows that QT is different from any such theory, and you have to give up either locality or determinism. Since local QFTs are the most successful consistent descriptions of matter we have today in terms of the Standard Model, my personal conclusion is that we have to give up determinism, but that was known since 1926 when Born got the so far only consistent interpretation of quantum states, namely their probabilistic meaning in terms of what we now rightly call "Born's Rule".
Again, you're missing the point which is to answer Mermin's challenge to explain how his device works to the "general reader." He's able to introduce the conundrum via the Mermin device in a way accessible to the "general reader," but I wasn't able to get the explanation quite down to that level. However, I did get it down to the level of someone who completed introductory physics. So, all you need from QM to do that are the quantum probabilities for the state in question — no Hilbert space, no density matrix, no Pauli spin matrices. The probabilities alone suffices to explain the mystery from the QM formalism. The first equation is a conventional way to write the correlation, so I'm surprised you don't recognize it. Anyway, since Unnikrishnan's conservation principle reproduces the quantum correlation (first equation plus QM probabilities), I have to translate the conundrum from probabilities to correlations. The spacetime or 4D view is necessary to justify Unnikrishnan's conservation principle as a constraint that fully resolves the conundrum, which I explain in Sec I.
Can you also explain this strange notation. Already the first equation is not clear to me. What does it mean? It's an average of what? What's in the numerator? In this way it's indeed a mystery compared to quantum theory, which is not a mystery but the solution to the mystery of the observed behavior of microscopic particles as well as the then ununderstandable stability of macrocsopic matter surrounding us.
That said, let me come to your AJP preprint. I'll got through it as I'd be a referee.
Section I is confusing and doesn't make sense to me to begin with.You should explain Mermin's apparatus to make your paper self-consistent. You don't explain it but rather open several other topics (4D spacetime views and Fermat's principle) which are completely unrelated to the "conundrum of entanglement". Since Bell it's the more clear that quantum theory is not the mystery but the solution to describe the behavior of subatomic particles, in this case spin-entangled states of two particles.
As a referee, I'd suggest to cancel Sect. I and use Sect. II as the introduction, explaining clearly Mermin's apparatus. You should explain what's entangled. It's the spins of the two particles emitted from the middle box. It doesn't make sense to say "two particles are entangled" in QM. You have to say which observables are entangled. Figs. 3 and 4 are unexplained. What are they good for? To make the paper understandable to at least a physics student who has heard the QM 1 lecture, you should just explain the experiment in terms of standard QT, i.e., say that the two spin-1/2 particles are prepared in the pure ##j=0##, ##j_3=0## state represented by the state vector
$$|Psi rangle=frac{1}{sqrt{2}} (|1/2,-1/2 rangle – |-1/2,1/2 rangle),$$
where the notation for the two-particle spin states is the usual one, i.e.,
$$|sigma_{z1},sigma_{z2} rangle equiv |sigma_{z 1} rangle otimes |sigma_{z2} rangle.$$
To make your paper as mysterious as you can you don't even tell this your reader anywhere.
What you describe then is completely ununderstandable to me. It doesn't reflect at all what QT predicts to be measured in A's and B's measurements. It's not clearly explained. You can calculate it easily of course. You simply quote the result in Eqs. (2) and (3) without clearly saying what's measured. Obviously what's meant is that A and B choose a plane (say the ##xy## plane for simplicity since due to the total isotropy of the entangled state it doesn't matter anyway which plane they choose). Then with two unit vectors ##vec{n}(alpha)=(cos alpha,sin alpha,0)## what's measured are the spin components of A's and B's particles in directions ##vec{n}(alpha)## and ##vec{n}(beta)## respectively. The probabilities quoted in Eqs. (2) and (3) are then, written in standard notation
$$P(sigma_{1alpha},sigma_{2beta})=|langle vec{n}(alpha) cdot vec{sigma}_1,vec{n}(beta) cdot vec{sigma}_2|Psi rangle|^2.$$
On the left-hand side of the equation I denoted spin components in direction ##alpha## in the above defined sense as ##sigma_{alpha}=vec{n}(alpha) cdot vec{sigma})##. I'll use this abbreviation from now on.
Of course the possible outcomes for each single-particle spin component are ##pm 1/2##, and you give the correct probs. for all four possible simultaneous outcomes in Eqs. (2) to (3). But why don't you give this simple explanation rather than the very complicated description so far?
Fig. 6 and its caption is absolutely enigmatic to me. I still don't get the meaning of the words "angular momentum is conserved on average" should mean for unaligned measurements, i.e., for ##alpha-beta neq 0## or ##pi##. In which sense should there be angular-momentum conservation be measured. I've brought this argument again and again already several times in this thread, and it's not answered. It doesn't even make sense in a classical context to check angular momentum conservation of a system by measuring components of angular momenta on different parts of the system in different directions! Also what's represented in this space-time diagram? Measurement outcomes of A's and B's measurements? Why do I need a space-time diagram to depict this?
I've no clue what ##langle alpha,beta rangle## should mean either. What's summed over? I can only guess it is
$$langle 4 sigma_{1 alpha} sigma_{2 alpha} rangle=sum_{sigma_{1 alpha},sigma_{2 alpha} =-1/2}^{+1/2} 4 sigma_{1 alpha} sigma_{2 alpha} P(sigma_{1 alpha}, sigma_{2 alpha}).$$
Then at least I can reproduce Eq. (4).
That Alice's and Bob's "spin angular momenta cancel on average" is the next mysterious statement. Do you mean that for any single-particle spin component the average is 0? That's of course true due to the complete isotropy of the spin-singlet state. Of course, this follows also from the probabilities given by Eqs. (2) and (3). Of course, everything is completely determined by the probabilities (2) and (3). So to translate the very complicated text, what you claim is that in some way you can get these quantum probabilities by a not precisely defined "principle of angular-momentum conservation on average"? I cannot invisage how I can make sense of that, although so far I could make some conjectures about what you wanted to say. As I repeatedly said, I've no clue what the fact that in this setup the single-particle spin components have a 0 expectation value to do with angular-momentum conservation.
That's trivial for the physical situation I guessed you really want to described, given the completely isotropic preparation of the two-particle state (the ##j=0## state). Formally you get the statistics of the single-particle spins by "tracing out the other particle", and this leads to
$$hat{rho}=frac{1}{2} hat{1}=frac{1}{2} left (|sigma_{alpha}=1/2 rangle langle sigma_{alpha}=1/2| + |sigma_{alpha}=-1/2 rangle langle sigma_{alpha}=-1/2| right )$$
for any ##alpha in [0,2 pi)##.
I'd be very interested, how your referee reports come out from AJP…:mad:
Ok, let me try to explain Unnikrishnan's conservation principle as transparently as possible. We have two sets of data, Alice's set and Bob's set. They were collected in N pairs with Bob's(Alice's) SG magnets at ##theta## relative to Alice's(Bob's). We want to compute the correlation of these N pairs of results which is
##frac{(+1)_A(-1)_B + (+1)_A(+1)_B + (-1)_A(-1)_B + …}{N}##
Now organize the numerator into two equal subsets, the first is that of all Alice's +1 results and the second is that of all Alice's -1 results
##frac{(+1)_A(sum mbox{BA+})+(-1)_A(sum mbox{BA-})}{N}##
where ##sum mbox{BA+}## is the sum of all of Bob's results corresponding to Alice's +1 result and ##sum mbox{BA-}## is the sum of all of Bob's results corresponding to Alice's -1 result. Notice this is all independent of the formalism of QM. Now, we rewrite that equation as
##frac{(+1)_A(sum mbox{BA+})}{N} + frac{(-1)_A(sum mbox{BA-})}{N} = frac{(+1)_A(sum mbox{BA+})}{2frac{N}{2}} + frac{(-1)_A(sum mbox{BA-})}{2frac{N}{2}}##
which is
##frac{1}{2}(+1)_Aoverline{BA+} + frac{1}{2}(-1)_Aoverline{BA-} ##
with the overline denoting average. Again, this correlation function is independent of QM formalism. All we have assumed is that Alice and Bob measure +1 or -1 with equal frequency at any setting in computing this correlation. Now we introduce our proposed conservation principle as I justified in #382 which is
##overline{BA+} = -cos(theta)##
and
##overline{BA-} = cos(theta)##
This gives
##frac{1}{2}(+1)_A(-cos(theta)) + frac{1}{2}(-1)_A(cos(theta)) = -cos(theta) ##
which is exactly the same correlation function as the quantum correlation obtained using conditional probabilities for the spin singlet state in QM. However, again, none of the QM formalism is used in obtaining this result. In deriving the quantum correlation function in this fashion, we assumed two key things: 1) Bob and Alice measure +1 or -1 with equal frequency in any setting and 2) Alice(Bob) says Bob(Alice) conserves angular momentum on average when Bob's(Alice's) setting differs from hers(his) by ##theta##. Those two assumptions are what I mean when I say the result is "reference frame independent."
I'll read your paper. It's a challenge to read about physics in terms of so much text and so few formulae ;-)).
I've still to read your AJP preprint, but please think about your understanding of conservation laws in quantum theory. It's obviously flawed. Physical quantities are frame independent by construction and as such conserved (or non-conserved) in any frame of reference!You’re still missing the point. I have a more explicit way to explain how this conservation of angular momentum on average yields the QM correlation (keep in mind, again, this principle is independent of the formalism of QM). It’s a bit long, so I’ll do that later today.
I've still to read your AJP preprint, but please think about your understanding of conservation laws in quantum theory. It's obviously flawed. Physical quantities are frame independent by construction and as such conserved (or non-conserved) in any frame of reference!
Well a key result is not argued, but is just asserted:
I don't see why that follows from conservation of angular momentum. Angular momentum conservation says that the two spins should add up to zero. When the measurements are along different axes, then getting the vectorial sum of the two measurements to be zero is impossible.So what is the motivation for replacing this impossible requirement by the requirement that ##(overrightarrow{S_1} + overrightarrow{S_2}) cdot overrightarrow{B} = 0##?
Note: as @vanhees71 says, spin measurements actually only give a number, not a vector, but I'm defining ##overrightarrow{S_1}## to be ##overrightarrow{A}## times the component of the spin of the first particle along axis ##overrightarrow{A}## and ##overrightarrow{S_2}## to be ##overrightarrow{B}## times the component of the spin of the second particle along axis ##overrightarrow{B}##.This is reference-frame-independent conservation of angular momentum, this is not your usual conservation of angular momentum. At some particular angle, Alice measures +1 and -1 (with equal frequency) over many trials. Consider all the trials where she measured +1 at that angle. She says her +1 result in each trial was the `right' value, i.e., the `true' magnitude of her particle's angular momentum ##vec{S1}##. Had Bob measured his particle at the same angle, he would have gotten -1 which is the `right' value at that angle, i.e., the `true' magnitude of his particle's angular momentum ##vec{S2}## for that trial. Instead, Bob measured at ##theta## relative to Alice, so he should only get a component of ##vec{S2}##, i.e., ##-cos(theta)##, which is less than 1. Unfortunately, Bob only measures +1 or -1 himself, so he can't get the `right' value (fraction) at ##theta## for any given trial. But, his +1 and -1 outcomes at ##theta## can average to the `right' value ##-cos(theta)##. Of course, the argument is symmetric, so Bob says the same thing about Alice's results.
So, who is measuring the `right' value of their ##vec{S}## for any given trial at ##theta## and who is only measuring the `right' value on average? Indeed, if each particle had a definitive (hidden) ##vec{S}## with magnitude S it would be amazing that Alice and Bob always measured +1 or -1. Why should that happen? Why don't they get random fractions of S? In Unnikrishnan's view, there is no underlying or hidden ##vec{S1}## and ##vec{S2}##. What Alice and Bob measure is all that is needed to give average conservation of angular momentum. No hidden variables, no `causal influences', all you need to invoke is reference-frame-independent conservation of angular momentum as just described and you get a correlation that equals that from QM.
Unnikrishnan shows how the quantum correlation function follows from conservation of angular momentum on average where the angular momenta measured by Alice and Bob are the angular momenta contributing to the conservation—not components. His derivation is independent of QM that’s why it’s interesting. It’s in my Insight. I don’t know what else to sayWell a key result is not argued, but is just asserted:
The average outcome for Alice’s set of +1 results is +1, so we expect that the average outcome of Alice’s results at ##theta## for that set would be ##cos(theta)##. Conservation of angular momentum therefore says Bob’s results corresponding to Alice’s set of +1 outcomes would average to ##- cos(theta)##I don't see why that follows from conservation of angular momentum. Angular momentum conservation says that the two spins should add up to zero. When the measurements are along different axes, then getting the vectorial sum of the two measurements to be zero is impossible.So what is the motivation for replacing this impossible requirement by the requirement that ##(overrightarrow{S_1} + overrightarrow{S_2}) cdot overrightarrow{B} = 0##?
Note: as @vanhees71 says, spin measurements actually only give a number, not a vector, but I'm defining ##overrightarrow{S_1}## to be ##overrightarrow{A}## times the component of the spin of the first particle along axis ##overrightarrow{A}## and ##overrightarrow{S_2}## to be ##overrightarrow{B}## times the component of the spin of the second particle along axis ##overrightarrow{B}##.
This you also get, of course, when measurin ##vec{S}_1 cdot vec{n}## and ##vec{S}_2 cdot vec{n}##, but a measurement of ##vec{S}_1 cdot vec{n}_1## and ##vec{S}_2 cdot vec{n}_2## with ##vec{n}_1 neq pm vec{n}_2## doesn't tell you anything about angular-momentum conservation.Unnikrishnan’s derivation of the quantum correlation doesn’t use QM. Read his derivation in my Insight or my AJP preprint, it’s very simple. It’s clear what he means by “conservation of angular momentum on average” by his derivation. I don’t know what else I can say
I just don't understand exactly how the quantum criterion follows from conservation of angular momentumUnnikrishnan shows how the quantum correlation function follows from conservation of angular momentum on average where the angular momenta measured by Alice and Bob are the angular momenta contributing to the conservation—not components. His derivation is independent of QM that’s why it’s interesting. It’s in my Insight. I don’t know what else to say
I cannot make sense of @RUTA 's ideas yet, maybe I get it by reading his preprint over the weekend, but within QT the issue is very clear.
Concerning #377: You cannot measure ##vec{S}=vec{S}_1+vec{S}_2##, nor ##vec{S}_1## or ##vec{S}_2##. You can measure always one component, say ##vec{S} cdot vec{n}## as well as arbitrary components ##vec{S}_1 cdot vec{n}_1## and ##vec{S}_2 cdot vec{n}_2##. If the particle pair is prepared in the spin-singlet state, i.e., if ##S=0## this implies that ##vec{S} cdot vec{n}=0## (exactly!!!) for all ##vec{n}##.
This you also get, of course, when measurin ##vec{S}_1 cdot vec{n}## and ##vec{S}_2 cdot vec{n}##, but a measurement of ##vec{S}_1 cdot vec{n}_1## and ##vec{S}_2 cdot vec{n}_2## with ##vec{n}_1 neq pm vec{n}_2## doesn't tell you anything about angular-momentum conservation. Of course, you get the correlations due to entanglement, and with clever arrangements for the directions you measure the spin you can verify the violation of Bell's inequality.
I just don't understand exactly how the quantum criterion follows from conservation of angular momentum.
In the EPR experiment with spin-1/2 twin particles, let ##overrightarrow{S_1}## be the measured spin of the first particle, and let ##overrightarrow{S_2}## be the measured spin of the second particle. We pick two directions ##overrightarrow{A}## and ##overrightarrow{B}## and we restrict our attention to those measurements such that
##overrightarrow{S_1} = + frac{1}{2} overrightarrow{A}##
##overrightarrow{S_2} = pm frac{1}{2} overrightarrow{B}##
The quantum prediction is that ##langle (overrightarrow{S_1} + overrightarrow{S_2}) cdot overrightarrow{B} rangle = 0## (where ##langle … rangle## means expectation value).
I don't see how conservation of angular momentum implies that ##langle (overrightarrow{S_1} + overrightarrow{S_2}) cdot overrightarrow{B} rangle = 0## Why is the sum ##overrightarrow{S_1} + overrightarrow{S_2}## projected onto the ##overrightarrow{B}## direction?
Of course QM produces the quantum correlation function. How else should I reproduce them?You're missing the entire point: Unnikrishnan's conservation of angular momentum on average reproduces the quantum correlations without using QM. That's why I said you're free to dismiss his conversation principle as "mere coincidence." It wouldn't be a coincidence if he had used QM.
The very point of Bell's ingeneous work was to show that local deterministic HV theories can't reproduce the correlations. So what's the goal of your investigation? Is it to find a non-local deterministic model/theory?Suppose you accept that Unnikrishnan's conservation of angular momentum on average is in fact a reasonable constraint responsible for the quantum correlations violating Bell's inequality, i.e., it's not just an amazing coincidence. In that case, you fall into the overwhelming majority of physicists who have discussed this with me. This conservation principle as a constraint is compelling. The question then is, do you require more? [This assumes you're not already content to "shut up and calculate."]
This conservation principle serves as the compelling constraint in and of itself, i.e., no 'deeper mechanism' a la hidden variables or 'causal influences' is required and none is offered. Do you require more? If so, you're just like Albert Michelson who said of his famous Michelson-Morley experiments, "It must be admitted, these experiments are not sufficient to justify the hypothesis of an ether. But then, how can the negative result be explained?'' In other words, even Michelson required some `deeper mechanism' to explain the light postulate of special relativity, i.e., why “the speed of light c is the same in all reference frames.'' Postulates, by definition, serve as the explanans (that which explains) not the explananda (that which is to be explained). Likewise here, if you require some `deeper mechanism' to explain the conservation of angular momentum on average, then this constraint is simply one mystery replacing another and cannot serve as a postulate or explanans.
That brings us to the theme of "Beyond the Dynamical Universe." Therein, we show over and over where physics understood via dynamical or causal mechanisms leads to mysteries that disappear when using constraints. So, this is yet another such example (see my Insights series Blockworld and its Foundational Implications). The point is, maybe it's time to ascend from the "ant's-eye view" of physical reality to the "4D view" of physical reality, as Wilczek challenged. Physics hangs together beautifully without "conundrums, mysteries, or paradoxes" when you do.