The Expert Physics and Math Blog

brownian motion

Brownian Motions and Quantifying Randomness in Physical Systems

/1 Comment/in /by

Stochastic calculus has come a long way since Robert Brown described the motion of pollen through a microscope in 1827. It’s now a key player in data science, quant finance, and mathematical biology. This article is drawn from notes I wrote for an undergraduate statistical physics course a few months ago. There won’t be any…

Trending Articles

Recent Entries

physics of reality

PBS Video Comment: “What If Physics IS NOT Describing Reality”

/
2 Comments
PBS Space Time produces some very good videos on the foundations of quantum mechanics (QM), so let me comment on their video What If Physics IS NOT Describing…
pvsnp

Aspects Behind the Concept of Dimension in Various Fields

/
2 Comments
Abstract It took until the last century for physicists and mathematicians in the Netherlands to question the Euclidean concept of dimension as length,…
complex numbers views

Views On Complex Numbers

/
70 Comments
Abstract Why do we need yet another article about complex numbers? This is a valid question and I have asked it myself. I could mention that I wanted…

Addition of Velocities (Velocity Composition) in Special Relativity

/
1 Comment
The "Addition of Velocities" formula (more correctly, the "Composition of Velocities" formula) in Special Relativity[tex]\frac{v_{AC}}{c}=\frac{ \frac{v_{AB}}{c}+\frac{v_{BC}}{c}…
Schrodinger's cat

Schrödinger’s Cat and the Qbit

/
27 Comments
The concept of quantum superposition (or superposition for short) is very counterintuitive, as Schr##\ddot{\text{o}}##dinger noted in 1935 writing [1],…
slinky drop experiment

The Slinky Drop Experiment Analysed

/
1 Comment
The slinky drop is a rather simple experiment. In its most basic form, it requires only a popular toy for children, a stable hand, and a keen eye.…
infinite universe

Is the Universe Finite, or Is It Infinite?

/
0 Comments
Standard cosmological models come in three flavors, open, flat, and closed,[Carroll] whose spatial curvatures are negative, zero, and positive. The open…
einstein field equations

All About the Einstein Field Equations

/
0 Comments
Definition/Summary The Einstein Field Equations (EFE) are a set of ten interrelated differential equations that form the core of Einstein's general theory…
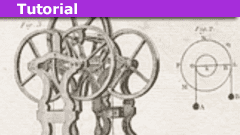
Multi-Atwood Machine Assembly

How to Solve a Multi-Atwood Machine Assembly

/
2 Comments
IntroductionThe figure on the right shows a "double-double" Atwood machine with three ideal pulleys and four masses.  All pulleys are released from…
Lambert W Function in Finance

The Lambert W Function in Finance

/
0 Comments
Preamble The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…
infinity

Why Division by Zero is a Bad Idea

/
33 Comments
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs: What if it was allowed? Then…
digital audio guide

Digital Filtering and Exact Reconstruction of Digital Audio

/
0 Comments
Introduction This elaborates some of the claims in my insights article on digital audio. The Sinc Function The first link in my insights article has…
digital audio intro

Introduction to Modern Digital Audio Concepts

/
0 Comments
IntroductionFirst, we need some background in Digital Signals. This can be mathematically quite advanced, but since I would like this…
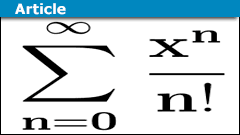
geometric series

Series in Mathematics: From Zeno to Quantum Theory

/
2 Comments
Introduction Series play a decisive role in many branches of mathematics. They accompanied mathematical developments from Zeno of Elea (##5##-th century…
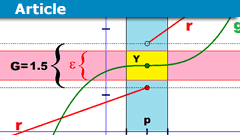
Epsilontic limits and continuity

Epsilontic – Limits and Continuity

/
1 Comment
Abstract I remember that I had some difficulties moving from school mathematics to university mathematics. From what I read on PF through the years, I…
Milli-Ohm

The Poor Man’s Milli-Ohm Meter

/
0 Comments
Introduction In a previous article on measuring battery internal resistance, a simple technique for low-resistance measurement was outlined. In this article,…
Differential Equation Systems and Nature

Differential Equation Systems and Nature

/
12 Comments
Abstract "Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…
calc precalc

Beginners Guide to Precalculus, Calculus and Infinitesimals

/
3 Comments
Introduction I am convinced students learn Calculus far too late.   In my view, there has never been a good reason for this.In the US, they go through…
Variable Mass Systems

How to Apply Newton’s Second Law to Variable Mass Systems

/
0 Comments
Introduction The applicability of Newton's second law in the oft-quoted "general form"  $$\begin{align}\frac{d\mathbf{P}}{dt}=\mathbf{F}_{\text{ext}}\end{align}$$…
what are numbers

What Are Numbers?

/
7 Comments
Introduction When doing mathematics,  we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive.   Going…
world of algebras

Introduction to the World of Algebras

/
0 Comments
Abstract Richard Pierce describes the intention of his book [2] about associative algebras as his attempt to prove that there is algebra after Galois…
chatgpt-reliable

Why ChatGPT AI Is Not Reliable

/
138 Comments
I'll start with the simple fact: ChatGPT is not a reliable answerer to questions.To try to explain why from scratch would be a heavy lift, but fortunately,…
Infinitesimals

What Are Infinitesimals – Simple Version

/
5 Comments
Introduction When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…
quantum information

How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics

/
0 Comments
In Chapter 37 of "The Feynman Lectures on Physics Volume 1," Richard Feynman famously wrote that the mystery of wave-particle duality in the double-slit…
Infinitesimals

What Are Infinitesimals – Advanced Version

/
0 Comments
Introduction When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…
Carl Sagan

When Pro Scientists Explain Using Pop Science

/
19 Comments
Abstract There is so much to say about the many endeavors by professional scientists to explain to us the world. The list is long: Carl Sagan, Harald…
art of integration

The Art of Integration

/
0 Comments
Abstract My school teacher used to say "Everybody can differentiate, but it takes an artist to integrate." The mathematical reason behind this phrase…
teaching physics

A Lesson In Teaching Physics: You Can’t Give It Away

/
1 Comment
A central principle of Physics Forums regarding homework help is not to provide solutions on demand but to guide students along a path to the answer.  The…
integration and complex differentiation

An Overview of Complex Differentiation and Integration

/
0 Comments
Abstract I want to shed some light on complex analysis without getting all the technical details in the way which are necessary for the precise treatments…
Measure Internal Resistance of Battery

How to Measure Internal Resistance of a Battery

/
0 Comments
Introduction A commonly encountered school-level Physics practical is the determination of the internal resistance of a battery - typically an AA or D…
lie group physics

When Lie Groups Became Physics

/
0 Comments
Abstract We explain by simple examples (one-parameter Lie groups), partly in the original language, and along the historical papers of Sophus Lie, Abraham…
white dwarfs

Why There Are Maximum Mass Limits for Compact Objects

/
0 Comments
In this article, we will look at why there are maximum mass limits for objects that are supported against gravity by degeneracy pressure instead of kinetic…
gravity collapse

Oppenheimer-Snyder Model of Gravitational Collapse: Implications

/
0 Comments
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn the last article in this series, we finished up with a metric for the Oppenheimer-Snyder…
tensors relativity

What Are Tensors and Why Are They Used in Relativity?

/
0 Comments
If you try learning general relativity, and sometimes special relativity, on your own, you will undoubtedly run into tensors. This article will outline…
gravity collapse

Oppenheimer-Snyder Model of Gravitational Collapse: Mathematical Details

/
0 Comments
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn a previous article, I described in general terms the model of gravitational…
twin paradox

When Discussing the Twin Paradox: Read This First

/
0 Comments
This article is intended for anyone who wants to start a thread here at Physics Forums on the twin paradox. There are already many, many threads here on…
gravity collapse

The Oppenheimer-Snyder Model of Gravitational Collapse: An Overview

/
0 Comments
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsMost people who have spent any time at all studying GR are familiar with the…
object slide down ramp physics

Subtleties Overlooked in Friction Questions: Object Slides Down Ramp

/
0 Comments
Problem statement (simplified) An object slides down a ramp at angle θ to encounter level ground. Both surfaces have kinetic friction: μ' on the ramp,…
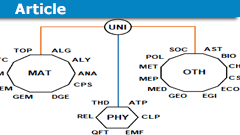
math classifications

Classification of Mathematics by 42 Branches

/
0 Comments
 I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what has…
recursion

Reduction of Order For Recursions

/
0 Comments
This is not meant as a full introduction to recursion relations but it should suffice for just about any level of the student.Most of us remember recursion…
history of numbers

Counting to p-adic Calculus: All Number Systems That We Have

/
0 Comments
An entire book could easily be written about the history of numbers from ancient Babylon and India, over Abu Dscha'far Muhammad ibn Musa al-Chwarizmi (##\sim…
evariste galois

Évariste Galois and His Theory

/
0 Comments
 * Oct. 25th, 1811  † May 31st, 1832 ... or why squaring the circle is doomed. Galois died in a duel at the age of twenty. Yet, he gave…
definition differences

Yardsticks to Metric Tensor Fields

/
1 Comment
I asked myself why different scientists understand the same thing seemingly differently, especially the concept of a metric tensor. If we ask a topologist,…
ATmega8A

Programming an ATmega8A using Arduino

/
2 Comments
If you are interested in programming and electronics, you probably do not need an introduction to Arduino. If you want to make your Arduino projects permanent,…
pvsnp

P vs. NP and what is a Turing Machine (TM)?

/
1 Comment
P or NP This article deals with the complexity of calculations and in particular the meaning of ##P\stackrel{?}{\neq}NP## Before we explain what P and…
quantum computers 101

Quantum Computing for Beginners

/
5 Comments
This article provides an accessible introduction to quantum computing, a cutting-edge technology that processes certain types of information much faster…
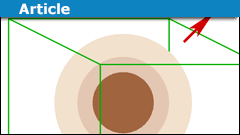
gauss law misconceptions

A Physics Misconception with Gauss’ Law

/
3 Comments
Introduction It is relatively common to see the following type of argument: The surface area is ##A## and the enclosed charge is ##Q##. The electric…
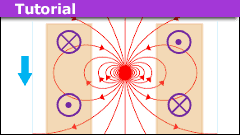
model magnet

How to Model a Magnet Falling Through a Conducting Pipe

/
7 Comments
Introduction In an earlier article, we examined a magnet falling through a solenoid. We argued that the point dipole model can account for the basic features…
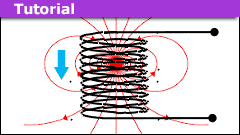
model magnet

How to Model a Magnet Falling Through a Solenoid

/
11 Comments
Introduction Modeling a magnet realistically is a task best done numerically.  Even the simplified model of two separated disks with uniform surface…
why can we jump

How Can We Jump When the Ground Does No Work?

/
20 Comments
It is relatively common on Physics Forums to see arguments that are effectively similar to the following: When we jump off the ground, the ground does…
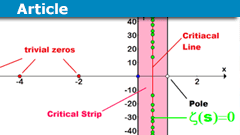
Riemann Hypothesis History

The History and Importance of the Riemann Hypothesis

/
0 Comments
Riemann Hypothesis History The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…