Physics w/ Calculus, Ch. 1 question: Vector Addition

[LearninDaMath]

This seems to be a very perplexing problem to which there is much difficulty of making sense of. So instead of trying to rewrite the problem in pieces, I've decided to provide the entire image leading up to the question so that you are seeing what I'm seeing. Hopefully, if I can describe where I'm having difficulty well enough, perhaps someone could provide some insight.

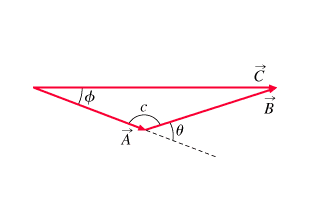
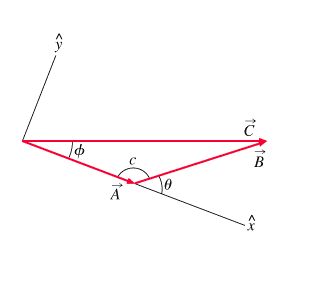
The problem, for the moment, is PART D.

The question: How do you get Csin\phi geometrically? That is, how do you get that answer by, "I think," using either or both of the first two equations (law of cosine and sin) instead of using the usual vector addition method?

 

[Spinnor]

Looking at the bottom picture, if I'm given C and phi then you have your answer. Are you confused how to get both C and phi, but then a quick look at your work-set looks like you are shown how to get both C and phi?

I'm confused with your confusion, %^) others might be as well. Could you state your problem in another way?

 

[Redbelly98]

The problem, for the moment, is PART D.

The question: How do you get Csin\phi geometrically? That is, how do you get that answer by, "I think," using either or both of the first two equations (law of cosine and sin) instead of using the usual vector addition method?

I'm not sure if I understand your question. The y-component of any vector is its magnitude, multiplied by the sine of the angle it makes with the +x axis. But surely you knew that already?

 

[Simon Bridge]

yep - geometrically, the trig relation follows from the definition of the sine.

You can get it from the law of sines as follows:

look at the big right-angled triangle with hypotenuse C and opposite side C_y the known angles are \phi, 90-\phi and 90 degrees.
By the sine-rule, therefore:

\frac{C_y}{\sin\phi} = \frac{C}{\sin(90)}

 

[SammyS]

I think I finally understand the question that's being asked. The screen shots in the opening post of this thread helped a great deal.

We have a vector equation:

\vec{A}+\vec{B}=\vec{C}\,,​

where the known quantities are the magnitudes of the vectors \vec{A} and \vec{B} and the angle, θ, between their directions.

The exercise in the screen shots, presumably from "Mastering Physics" is taking you through steps which can show the equivalence of two methods for finding and describing the resultant vector, \displaystyle\vec{C}\,.

One method -- the 'Geometry Method' -- mainly uses the Law of Cosines and the Law of Sines along with plane geometry to find the magnitude of \displaystyle\vec{C} along with its direction relative to the direction of \displaystyle\vec{A}\,.

The other method -- the Component Method -- uses elementary trigonometry to find the components of \displaystyle\vec{A} and \displaystyle\vec{B} then adding them to describe \displaystyle\vec{C} via its components.​

That the two methods give the same magnitude for \displaystyle\vec{C} is dealt with in Parts B & C.

We see in Part D that they begin with geometry giving the result \displaystyle C_y=\left|\vec{C}\right|\sin(\phi)\,. Obviously the component method gives \displaystyle C_y=\left|\vec{B}\right|\sin(\theta) \,. (See Item 4 on the first panel of the screen shots.) As I see it, the rest of the exercise is to show that these expressions for C_y are equivalent. This can be done using the Law of Sines for the triangle formed by the three vectors, \vec{A}\,,\ \vec{B}\,,\ \text{and }\vec{C}\,.

 

[Simon Bridge]

This is what I was thinking from this thread, and others - OP has misunderstood what the papers in the screenshots are telling him to do. That's why we've been floundering around.

Had OP started out with this thread (i.e. had he asked about the problem he actually had instead of trying to talk around it) it would have been apparent sooner.

You can also run the proofs through elementary trig, or by noticing that c=\pi - \theta too.

What the exercise in the green box is effectively asking for is the conversion between polar and cartesian coordinates.
(That the polar and cartesian representations of C given are the same.)