- #1
mathzeroh
- 98
- 0
OK this problem has been giving me nonstop headaches and nightmares for over 4 days! 
I just can't seem to understand something here!
Here's the actual problem:
Suppose that you have 80 feet of fence to enclose a garden. For each garden design below, find the dimensions of the garden which produce the maximum area. The "bold" lines indicate where the fence must go. Note: diagrams below not to scale.
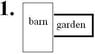
1. Barn on one side. No fence necessary there.
max area = _______________
2. Garden with fence divider in the middle, barn on one side.
max area = _______________
3. No barn, fence on all four sides, and two center dividers.
max area = _______________
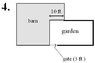
4. L - shaped barn used for one side and 10 ft. of the other side. No fence required for 3 ft. gate.
max area = _______________

I just can't seem to understand something here!
Here's the actual problem:
Suppose that you have 80 feet of fence to enclose a garden. For each garden design below, find the dimensions of the garden which produce the maximum area. The "bold" lines indicate where the fence must go. Note: diagrams below not to scale.
1. Barn on one side. No fence necessary there.
max area = _______________
2. Garden with fence divider in the middle, barn on one side.
max area = _______________
3. No barn, fence on all four sides, and two center dividers.
max area = _______________
4. L - shaped barn used for one side and 10 ft. of the other side. No fence required for 3 ft. gate.
max area = _______________
 thanks man!
thanks man! 
