- #1
ecneicS
- 64
- 0
Homework Statement
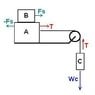
Block B, with mass 5.00kg, rests on block A, with mass 8.00kg , which in turn is on a horizontal tabletop. There is no friction between block A and the tabletop, but the coefficient of static friction between block A and block B is 0.750. A light string attached to block A passes over a frictionless, massless pulley, and block C is suspended from the other end of the string.
Homework Equations
F=ma
FFriction = μN
The Attempt at a Solution
What makes sense for me to do is to find the tension in the string which I think is equal to the force due to gravity on block C. What throws me off is that the force of friction between B and A is in the same direction of the Tension force of the string.
I tried to set up a net force equation of B and got
F = FgravityonC - Ffriction = 0
But then the answer I get (3.75kg) is wrong. I'm not convinced that FgravityonC is supposed to be in the equation. And I haven't addressed block A at all.
Please give me a prod in the right direction!