- #1
bulbasaur88
- 57
- 0
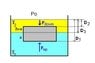
A sphere of density = 500 kg/m^3 floats on water (density of water = 1000 kg/m^3).
1. What fraction of the volume of the sphere is below the waterline?
---I understand this problem and I got the correct answer of 0.5
2. Another liquid of density 200 kg/m^3 is now added on top of the water. The second liquid will not mix with the water. What fraction of the volume of the sphere is now below the waterline?
--The answer is supposed to be 3/8.
I have been trying to find out how to do this for a long time, and I still do not understand how to figure it out but I have an inkling it will be on my final exam in a week! Please help me sound this out. Thank you!
1. What fraction of the volume of the sphere is below the waterline?
---I understand this problem and I got the correct answer of 0.5
2. Another liquid of density 200 kg/m^3 is now added on top of the water. The second liquid will not mix with the water. What fraction of the volume of the sphere is now below the waterline?
--The answer is supposed to be 3/8.
I have been trying to find out how to do this for a long time, and I still do not understand how to figure it out but I have an inkling it will be on my final exam in a week! Please help me sound this out. Thank you!