- #1
Casquibaldo
- 10
- 0
Homework Statement
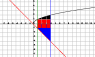
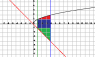
Set up sums of integrals that can be used to find the area of the region bounded by the graphs of the equations by integrating with respect to y.
y= sqrt(x) y=-x x=1 x=4
Homework Equations
∫[f(x) - g(x)] dx
The Attempt at a Solution
I did:
∫ (from 1 to 4) [sqrt(x) + x] dx and worked it out to get 73/6, but my friend said I'm doing it backwards and doesn't want to explain. If anyone could tell me what I'm doing wrong, I would be grateful.