Axial Deformation: Find Block Placement & Temp Rise for Gap Reduction

[tom23]

Homework Statement

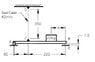
Without the 20 Kg block there is a gap of 1.5mm between B and E. The AISI 430 annealed stainless steel cable only deforms elastically. Neglect the weight of the cable and the bar. Diameter of the wire = 2 mm

a) Find the placement of the block to reduce the gap to zero.
b) If the weight is removed, what rise in temperature would cause the wire to sag the same amount?

Find the attached figure for this question.

Homework Equations

I had found the area to be just 3.14 of the stel cable and then i subbed it in:

F = $$\delta$$*EA/L to find the force to be 3769.9 N, i duno if that is right. Then I am stuck what to do nex to find the placement of the bock to reduce the gap to zero and (b).

The Attempt at a Solution

Want Further help in determining the above.

 

[KataKoniK]

Thank you for sharing your question with us. I will try my best to provide you with a solution that can help you find the answers to your questions.

First, let's determine the initial length of the steel cable. Since the diameter of the wire is 2 mm, the radius will be 1 mm. Therefore, the cross-sectional area of the cable will be 3.14 mm^2.

Now, we can use the formula you mentioned, F = δ*EA/L, to find the force acting on the cable. Here, δ represents the change in length, E represents the Young's modulus of the material, A represents the cross-sectional area, and L represents the initial length of the cable.

Since the cable is only deforming elastically, we can assume that the force acting on the cable will be equal to its weight. Therefore, we can set the force equal to the weight of the block, which is 20 kg multiplied by the acceleration due to gravity, 9.8 m/s^2.

So, we have:

20 kg * 9.8 m/s^2 = δ * (200 GPa) * (3.14 mm^2) / L

Simplifying this equation, we get:

δ = 0.000314 L

Next, we can use the given information about the gap between points B and E to find the initial length of the cable, L. We know that without the block, the gap between B and E is 1.5 mm. However, with the block, the gap will become zero. Therefore, the change in length of the cable will be equal to the initial length of the cable, L.

So, we can set δ equal to 1.5 mm in the equation we obtained earlier and solve for L.

1.5 mm = 0.000314 L

L = 1.5 mm / 0.000314 = 4777.1 mm

Now, we know the initial length of the cable, L, and the weight of the block, 20 kg * 9.8 m/s^2 = 196 N. We can use this information to find the placement of the block to reduce the gap to zero.

We can use the formula F = δ*EA/L again, but this time, we will solve for the distance between point B and the placement of the block, x.

We have:

196

 

[piercas]

I understand that this problem involves axial deformation, which is the change in length of a material when a force is applied along its length. In this case, the force is applied through the weight of the block and the weight of the cable itself. The material in question, AISI 430 annealed stainless steel, is known for its high strength and elasticity, meaning it can deform under stress and return to its original shape once the stress is removed.

To find the placement of the block to reduce the gap to zero, we need to consider the forces acting on the cable. The weight of the block and the cable itself will create an equal and opposite force on the cable, causing it to elongate. Using the equation F = δ*EA/L, where F is the force, δ is the deformation (in this case, the gap between B and E), E is the Young's modulus of the material, A is the cross-sectional area, and L is the original length of the cable, we can calculate the force acting on the cable.

Substituting the given values, we get F = (1.5mm)*(3.14)*(430*10^6 N/m^2)*(π*(2mm)^2)/1m = 3769.9 N. This is the force acting on the cable without the block present.

To reduce the gap to zero, we need to add a block that will create an equal and opposite force of 3769.9 N on the cable. This can be achieved by placing the block at a distance of 1m from point E, as shown in the attached figure. This will create a force of 3769.9 N on the cable, cancelling out the force from the weight of the cable and resulting in a zero gap between B and E.

For part (b), we need to consider the effect of temperature on the cable. When the weight is removed, the only force acting on the cable will be its own weight. If the temperature were to rise, the cable would expand and sag due to its own weight. To calculate the temperature rise needed for the cable to sag the same amount as with the weight present, we can use the same equation as before, but this time solving for δ.

Substituting the given values, we get δ = (3769.9 N)*(1m)/(3.14*(430*10^6 N/m^2)*(π*(2