- #1
fysik
- 73
- 0
hello
The below structure (the triangle) is connected to fixed point A that is a hinge (can rotate freely).
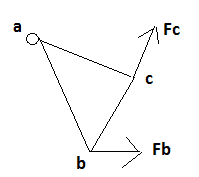
Fc force is perpendicular to (ac) and Fb is horizontal. If the (bac) angle is 30 degrees, calculate the reaction at A.
My attempt:
Since Fc is perpendicular to (ac) it doesn't apply any force across the line (ac) so it doesn't create any reaction at a.
Fb creates a reaction at a, since if we analyse it in two axis (the ab axis and the perpendicular to ab) a part of it (across the ab axis) creates a reaction (the same but with different direction) and the perpendicular to (ab) part does not create any reaction at a at all.
But how to find the part of Fb on the (ab) axis?
And is my approach correct?
Thanks
The below structure (the triangle) is connected to fixed point A that is a hinge (can rotate freely).
Fc force is perpendicular to (ac) and Fb is horizontal. If the (bac) angle is 30 degrees, calculate the reaction at A.
My attempt:
Since Fc is perpendicular to (ac) it doesn't apply any force across the line (ac) so it doesn't create any reaction at a.
Fb creates a reaction at a, since if we analyse it in two axis (the ab axis and the perpendicular to ab) a part of it (across the ab axis) creates a reaction (the same but with different direction) and the perpendicular to (ab) part does not create any reaction at a at all.
But how to find the part of Fb on the (ab) axis?
And is my approach correct?
Thanks