Calculating Current in a Circuit with a 20 Ohm Resistor

[mopar969]

How do you find the current that flows through the 20 ohm resistor? See attached pdf for picture

 

[gneill]

There are several possible approaches. What circuit analysis techniques have you studied so far? Any transformations like Thevenin equivalents?

 

[mopar969]

I only learned how to do series and parallel and cramers rule. I believe I need to use cramers rule here but I am having trouble getting started.

 

[WatermelonPig]

The voltage around a closed loop is 0. There are three possible loops here. Maybe set up a 3x3 matrix.

 

[gneill]

Cramer's rule will help if you can write the Kirchhoff's loop equations for the circuit. There are three obvious loops. Can you write the KVL equations for them?

 

[mopar969]

I have the four junctions that I made:
J1: I2 = I3 +I6
J2: I3=I4
J3: I6+I4=I5
J4: I5=I2

I am having trouble seeing how the other two loops connect back to the battery but here is what I have so far:
Loop 1: -20v = 4I2+1I3

 

[gneill]

Here's you circuit again with the (suggested) three loops indicated:

 

[mopar969]

My question is what is the voltage for loops 2 and three since they do not go through the power supply?

 

[gneill]

My question is what is the voltage for loops 2 and three since they do not go through the power supply?

There are no voltage sources in those loops. The currents are driven by the influence of loop 1. Nevertheless, the sum of the voltage drops around each loop obeys KVL. Just write the loop equations for what components are in the loops.

 

[mopar969]

So here is what I now have:

I have the four junctions that I made:
J1: I2 = I3 +I6
J2: I3=I4
J3: I6+I4=I5
J4: I5=I2

I am having trouble seeing how the other two loops connect back to the battery but here is what I have so far:
Loop 1: -20v = 4I2+1I3
Loop 2: 0 = 4I2+20I6+3I5
Loop 3: 0 = 1I3+6I4-20I6

Are these correct and thanks for the diagram help.

 

[gneill]

You can solve the problem with just three KVL loop equations, solving for the KVL loop currents. You seem to have written equations with a LOT of different currents.

To write the equations, you "walk" around each loop summing up the voltages rises and drops due to the KVL loop currents that flow through each component and voltage supplies (if any).

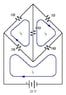
Numbering the KVL loop currents as I showed in the diagram, a loop equation for loop 2 is,

3*(i1 - i2) - 4*i2 + 20*(i3 - i2) = 0

Or, collecting together the current variables,

i1*3 - i2*(3 + 4 + 20) + i3*20 = 0

Can you write the same sort of loop equations for loops 1 and 3?

 

[mopar969]

I thought that the current changes at each junction that is why I have up to I6. Why doesn't this occur?

 

[gneill]

I thought that the current changes at each junction that is why I have up to I6. Why doesn't this occur?

If you're doing a nodal analysis then you have to give each branch its own current. In KVL you assign a single current to each loop. If there are three loops, there are three independent currents.

Note that when components are shared by loops, then the currents belonging to both loops flow through those components (and always in opposite directions if you draw each loop current with the same orientation either CW or CCW).

 

[mopar969]

How do you determine in you picture if I is negative and positive. Also, what did you use to draw the picture that can come in handy for me? Thanks again for all the help.

 

[gneill]

The loop current directions are arbitrary. I tend to always draw them in a clockwise direction. The 'real' directions of the currents will take care of themselves in the algebra, so don't be surprised if some loop currents end up with negative values -- that just means that the true direction is opposite to that assumed. I find that consistency is better than clever guessing, and leads to fewer mistakes.

I use Visio to make my drawings, then paste them into Paint to save them as JPEGs.

 

[mopar969]

I understand what you mean but in your equation for loop two how did you determine that 4I2 was negative and that 20I2 was negative?

 

[gneill]

I understand what you mean but in your equation for loop two how did you determine that 4I2 was negative and that 20I2 was negative?

I take it that when "walking" through a resistor in same direction as a current, there will be a potential drop. So in this case, following current i2 through the 4 Ohm resistor, there is a voltage drop of i2*4. A drop is negative. A rise is positive. It is similar for following i2 through the 20 Ohm resistor.

Note that the 20 Ohm resistor also has i3 flowing through it. In that case, when you "walk" around loop 2 in the direction of i2, the current i3 is flowing in the opposite direction in the 20 Ohm resistor, so i3 will cause a voltage rise across that resistor from the perspective of "loop 2 traveler". So you get a +i3*20 term for that.

 

[mopar969]

The equations that I got for loops 1 and three using your diagram are
Loop1: -20 = 3(I1-I2)+6(I1-I3)
Loop3: 0=I3+6(I1-I3)+20(I3-I2)

Now where do I go with the problem? Do I have to set up my four junction equations?

 

[gneill]

Good effort. A couple of small points though. For Loop1, the voltage should be positive on the LHS of the equation, and for Loop3, the second term should be 6(I3 - I1).

So your three equations should look like:

Loop1: 20V = 3(i1 - i2) + 6(i1 - i3)
Loop2: 0 = 3(i2 - i1) + 4i2 + 20(i2 - i3)
Loop3: 0 = 1i3 + 6(i3 - i1) + 20(i3 - i2)

That's all you need to solve for the loop currents i1,i2, and i3. Three equations in three unknowns. You can use substitution or set up Cramer's rule.

Once you have the currents, to find the current through the 20 Ohm resistor just take note of which loop currents flow through it and add accordingly.

 

[mopar969]

I do not know how to do cramers rule but I tried substitution and did not get anything to cancel to one term.

 

[gneill]

Hmm. I thought you knew how to use Cramer's rule. Well, you have three equations in three unknowns so it should just be a matter of algebra. You'll have to show your work in order for us to see where it's going wrong.

 

[mopar969]

I I think I found my error by using substitution and I now got
I1 = 670/39
I2 = 10/39
I3 = 740/39

Are these correct and if so how do I now go about finding the current that flows through the 20 ohm resistor?

 

[gneill]

Your values don't look right. Some of the numbers in the fractions look as though they belong though... so it's likely just a small error that's tripping you up. Why don't you post the steps?

 

[mopar969]

Sorry I was looking at another problem of mine when I typed that the answers I got were
I1 = 80/33
I2 = 10/3
I3 = 10/33

 

[gneill]

No, that's not correct either. I think you'd best post your solution steps.