- #1
procol
- 5
- 0
Homework Statement
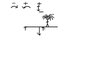
A plank is supported from two points. How far can a gril that weights 48 kg walk on the plank before the plank starts to rotate?. Middle of plank is its gravity point.
Picture: I have added a picture that might tell a bit more(not so good at English :/)
https://www.physicsforums.com/attachment.php?attachmentid=24296&stc=1&d=1268318353
m1= mass of the plank = 80kg
m2= mass of gril = 48kg
L plank = 5m
Support point A= 2.5m from center of plank mass/gravity
Support point B= 0.3m from center of plank mass/gravity
Homework Equations
Summ F=0
Summ M=0
G=mg
M=Fr
The Attempt at a Solution
I have tryed a few equitions but have not had any luck.
Na= support point A
Nb= support point B
Gp= Plank gravity center
Gg= Girl Gravity
Na+Nb-Gp-Gg=0
Thx for Help