Calculating Work Done by a Rope on a Sled

[kbyws37]

A sled is dragged along a horizontal path at a constant speed of 1.5 m/s by a rope that is inclined at an angle of 30.0° with respect to the horizontal (see the figure below). The total weight of the sled is 470 N. The tension in the rope is 250 N. How much work is done by the rope on the sled in a time interval of 5.00 s?

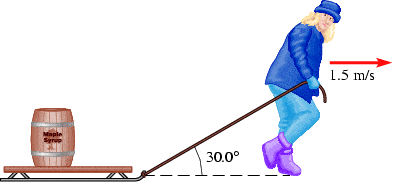
I'm not sure if I'm on the right track.
I'm using the equation
W=K+U =E
E = (mv^2)/2 + mgy
but i don't know where I would put time and where

250cos(30) would go.

or maybe I'm just totally off.

 

[Hootenanny]

Think about the definition of work done (in terms of force).

 

[radou]

You know the velocity, and you know the time. So, you know the displacement, too. I'm sure you'll know how to carry on from this point.

 

[kbyws37]

I used x = ((Vi + Vf)t)/2 and found the displacement to be 3.75
Then I used the equation:

E = (mv^2)/2 + mgx = W
= ((470)(1.5^2))/2 + ((470)(9.8)(3.75))
= a huge number (which is not correct)

If i use the equation
W = F*x*cos()
W = 470*3.75*cos(30)
W = 1526.37
which says that I am wrong

 

[radou]

I used x = ((Vi + Vf)t)/2 and found the displacement to be 3.75

Ever heard of the simple expression for constant velocity $$x = v\cdot t$$?

 

[Hootenanny]

I used x = ((Vi + Vf)t)/2 and found the displacement to be 3.75

Although radou's equation is simpler to use your equation above is valid. If you substitute in the the correct values you should obtain the correct answer. However, 3,75 is not correct. The rest of your working;

If i use the equation
W = F*x*cos()

Looks good except for the erroneous value for displacement.