- #1
brainbaby
- 228
- 5
Hi guys
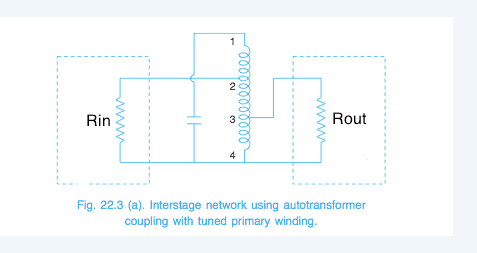
As per text...
To match 10k with 500Ω a coil is used as an autotransformer tapped at point 3...now for a certain bandwidth and centre frequency what should be the value of Lp and Ls...?? How do I calculate it..??
and
if the value of Ls and Lp is found out to be low then how could they be increased by using tapping to yield a high value of Q..??
Thanks in advance
As per text...
To match 10k with 500Ω a coil is used as an autotransformer tapped at point 3...now for a certain bandwidth and centre frequency what should be the value of Lp and Ls...?? How do I calculate it..??
and
if the value of Ls and Lp is found out to be low then how could they be increased by using tapping to yield a high value of Q..??
Thanks in advance