Conservation of Momentum in Partially Elastic Collisions: Solving for Velocity

[Kishlay]

Homework Statement

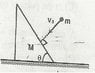
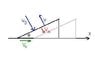
In the figure shown, a ball of mass m collides perpendicularly on a smooth stationary wedge of mass M, kept on a smooth horizontal plane. If the coefficient of restitution of collision is e, then determine the velocity of the wedge after collision.

Homework Equations

can we conserve momentum when the collision is partially elastic ?

The Attempt at a Solution

i wrote→ mV°sinθ= MV + meV°sinθ
is this right??

 

[CWatters]

Momentum is conserved in both Elastic and Inelastic collisions.

 

[Kishlay]

yes but how in this case??

 

[Kishlay]

Momentum is conserved in both Elastic and Inelastic collisions.

this is partially elastic collision, value of e is not known to you...

 

[haruspex]

i wrote→ mV_°sinθ= MV + meV_°sinθ

The ball's velocity after impact is not eV₀.
What is the definition of the coefficient of restitution?

 

[Kishlay]

this is e...

 

[haruspex]

this is e...

OK, except that there should be a minus sign because the relative velocity will reverse.
In the present problem it's a bit tricky to apply because of the different directions involved. You know the relative velocity before collision, but what should you take as the relative velocity afterwards? Any thoughts?

 

[Kishlay]

yes... the relative velocity will be respect to ground frame...!

 

[haruspex]

yes... the relative velocity will be respect to ground frame...!

Relative velocity doesn't need a frame. Or, if you prefer, it's the velocity of the one object in the frame of the other.

 

[haruspex]

I don't know whether this is still of interest to you, but I have concluded that you cannot solve it using the definition of CoR in the usual way. There is no appropriate relative velocity after the collision. Instead, use the way in which the CoR affects the recovered energy.
Treating the collision as compression of a spring, there comes a point at which compression is a maximum. At that point, the ball and the wedge have the same velocity in the direction of travel of the ball. You can work out (but it's not easy) what fraction of the original KE is now stored as PE. The affect of the CoR being < 1 is that not all of the PE is recovered again as KE. The fraction that is recovered is e². This allows you to work out how much energy is lost. Fwiw, I get lost energy = $\frac{(1-e^2)M}{M+m\sin^2(\theta)}$

 

[Kishlay]

ya that seems to be a bit tricky...but how this going to help me??

 

[Kishlay]

this question is very hard...!

 

[tiny-tim]

Hi Kishlay!

I don't see the difficulty …

Call the speeds after v and V.

Write out the coefficient of restitution formula for v and |V - v|.

Do conservation of momentum in the horizontal direction (because there are no external forces in that direction) …

what do you get? ​

 

[haruspex]

Call the speeds after v and V.

Write out the coefficient of restitution formula for v and |V - v|.

I very much doubt that is valid in the context of this problem. It ignores the contribution of the reaction from the ground.

 

[tiny-tim]

I very much doubt that is valid in the context of this problem. It ignores the contribution of the reaction from the ground.

the question doesn't give a coefficient of restitution between the block and the ground, so i think we're intended to apply the formula only to the interaction between the block and the ball

 

[haruspex]

the question doesn't give a coefficient of restitution between the block and the ground, so i think we're intended to apply the formula only to the interaction between the block and the ball

I made that assumption already (which I should have made explicit). If you think the relative velocity ratio can be applied, please state exactly what two velocities you would take for after the collision.
As far as I am aware, Newton's Experimental Law is for two-body collisions. Newton found that for a given pair of objects the relative velocity ratio was constant. Initially this was just head-on collisions, but it's reasonably obvious how to extend it to oblique ones.
In the CoM frame of reference, one can deduce that the fraction of energy conserved is e². Thinking about the physics, it becomes clear that this is the fundamental fact: of the PE stored in the compression phase, a fixed fraction is released back to become KE. So NEL is a consequence, not a physical fundamental.
It follows that the method I used to solve the problem is reliable and valid in the OP context. If you think you have a way to do it using velocity ratios it will need to produce the same answer.

 

[ehild]

If you think you have a way to do it using velocity ratios it will need to produce the same answer.

The ratio of the final to initial KE in the COM reference is exactly the square of the ratio between the speeds.

ehild

 

[haruspex]

The ratio of the final to initial KE in the COM reference is exactly the square of the ratio between the speeds.

ehild

Yes, that is the test I am proposing of whether the two selected speeds are valid, but what two speeds are you going to pick?

 

[ehild]

Speed of approach is vo
Speed of separation is $|\vec v_{ball} -\vec V_{wedge}|$ with velocity vectors after the impact.

ehild

 

[haruspex]

Speed of approach is vo
Speed of separation is $|\vec v_{ball} -\vec V_{wedge}|$ with velocity vectors after the impact.

ehild

That doesn't even work for an oblique two ball collision, let alone the three body case we have here.

 

[TSny]

Fwiw, I get lost energy = $\frac{(1-e^2)M}{M+m\sin^2(\theta)}$

I agree with this result for the fractional energy loss. I got an answer for the final speed of the wedge, without considering energy, by using the definition of CoR as the ratio of restoration impulse to deformation impulse. See for example, page 8 here

You can use this definition to show that in this problem the CoR is equal to the ratio of the relative speed of separation along the line of impact (i.e., perpendicular to the plane) to the relative speed of approach along the line of impact.

 

[haruspex]

I agree with this result for the fractional energy loss. I got an answer for the final speed of the wedge, without considering energy, by using the definition of CoR as the ratio of restoration impulse to deformation impulse. See for example, page 8 here

You can use this definition to show that in this problem the CoR is equal to the ratio of the relative speed of separation along the line of impact (i.e., perpendicular to the plane) to the relative speed of approach along the line of impact.

Thanks! I thought I tried that velocity ratio but got a different answer. Must have made a mistake, I'll check. It bothered me that the impulse from the ground has a component in that direction.

 

[Kishlay]

when you all guys talk like this, it makes me feel that i am like nothing ...;)

 

[tiny-tim]

Kishlay, did you try …

Call the speeds after v and V.

Write out the coefficient of restitution formula for v and |V - v|.

Do conservation of momentum in the horizontal direction (because there are no external forces in that direction) …

what do you get? ​

 

[ehild]

Kishlay, there are lot of confusion in regards the coefficient of restitution, how did your professor explained it?

ehild

 

[haruspex]

Call the speeds after v and V.

Write out the coefficient of restitution formula for v and |V - v|.

I confirm TSny's result. You have to take only the component of the wedge's velocity normal to its sloping surface. Still not sure I've grasped that intuitively, but it does give the right answer. Your method will not.

 

[ehild]

Kishlay, see figure attached.

The wedge will move horizontally to the right with speed Vx, but its surface displaces with the normal velocity Vn . If the ball bounces back from the surface with velocity v, the relative speed of separation is |V_n-v|. With the magnitudes, it is V_n+v. So

e=(V_n+v)/v₀.You can see that the horizontal speed of the wedge is related to the normal speed of the surface as V_n=V_xsinθ.

Apply conservation of momentum for the x components of the velocities.

You get two equations for v and V_x. Eliminate v, and solve for V_x.

ehild

 

[Kishlay]

please see below...

 

[Kishlay]

Kishlay, see figure attached.



e=(V_n+v)/v₀.

i think there will be a -ve sing right?

 

[ehild]

I meant v the speed of the ball after collision. The relative velocity of the ball with respect to the surface of the wedge is Velocity(ball) - Velocity (wedge). The ball and wedge surface move in opposite direction, so their speeds add, the speed of separation is the sum of speeds Vn and v.

ehild