- #1
TheColector
- 29
- 0
Hi there
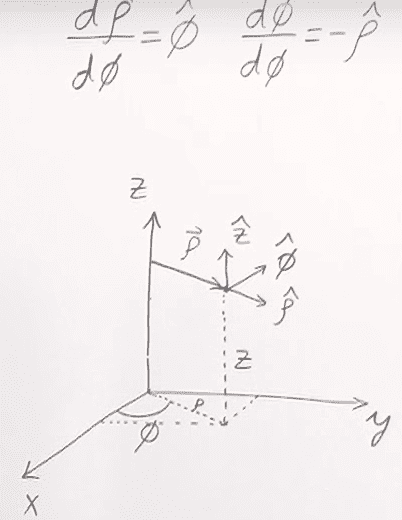 A picture attached for visualization.
A picture attached for visualization.
3.
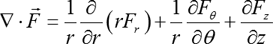 General formula
General formula
Thanks for any help.
- I'm having a hard time trying to understand how come ∂r^/∂Φ = Φ^ ,∂Φ/∂Φ = -r^ -> these 2 are properties that lead to general formula.
- I've been thinking about it and I couldn't explain it. I understand every step of "how to get Divergence of a vector function in Cylindrical Coordinates" except for these formulas below.
3.
Thanks for any help.